Ὁ τετραγωνισμὸς τοῦ κύκλου στὸ Πὶ καὶ Φί
Θεμελιώδης Συμπαντικὸς Λόγος
Ἀπό τὸ βιβλίο…

Ἀναφερόμενοι στὸ Σύμπαν, ἂς θεωρήσουμε ὅτι ἡ ὀρθὴ τιμὴ τοῦ ἀριθμοῦ π εἶναι ὁ ἀριθμὸς πφ.
Ἂς θεωρήσουμε ἐπίσης ὅτι ἡ ταχύτητα τοῦ φωτὸς εἶναι παγκόσμια σταθερὰ (ἀναλλοίωτη) καὶ ὅτι αὐτὴ εἶναι ἴση μὲ c=299.792.465km/sec ὅπως ἔχει μετρηθεῖ.
Ἂς βάλλουμε τέλος μιὰ ἐξαίρεση στὴ ρήση τοῦ Ἡράκλειτου «ΤΑ ΠΑΝΤΑ ΡΕΙ». Αὐτή, ἂς εἶναι τὸ σημεῖο τοῦ BIG BANG (τῆς Μεγάλης Ἔκρηξης), ὡς τὸ μοναδικὸ σημεῖο ποὺ δὲν κινεῖται στὸ Σύμπαν.
Θεωροῦμε ὅτι Γῆ καὶ Ἥλιος βρίσκονται συνεχῶς σὲ ἐπίπεδο κάθετο μὲ τὴν διεύθυνση κίνησης τους, λόγω διαστολῆς τοῦ Σύμπαντος. Ἔστω πὼς ἕνας παρατηρητὴς Α βρίσκεται ἐπίσης στὸ ἴδιο ἐπίπεδο καὶ σὲ ἀπόσταση ρ, ἀπὸ τὸ κέντρο τοῦ Ἥλιου. Γιὰ νὰ γίνει πιὸ κατανοητό, θεωροῦμε ὅτι ἡ ἀπόσταση ρ εἶναι ἴση μὲ τὴν ἀπόσταση τῆς Γῆς ἀπὸ τὸ κέντρο τοῦ Ἥλιου.
Ὁ παρατηρητὴς Α θέλει νὰ μετρήσει τὴν περίμετρο τοῦ κύκλου ποὺ δημιουργεῖται μὲ ἀκτίνα ἴση μὲ τὴν ἀπόσταση του ἀπὸ τὸ κέντρο τοῦ Ἥλιου καὶ μὲ τὸ κέντρο τοῦ κύκλου νὰ ταυτίζεται μὲ τὸ κέντρο του Ἥλιου. Θέλει ἐπίσης νὰ ὑπολογίσει καὶ τὴν ἀκτίνα του.
Γιὰ νὰ μπορέσει νὰ μετρήσει τὴν περίμετρο θὰ χρησιμοποιήσει τὸν καταλληλότερο μετρητὴ μεγάλων ἀποστάσεων. Αὐτὸς θὰ κινεῖται μὲ τὴ μέγιστη ταχύτητα τοῦ φωτός.
Ἂν θέλουμε μποροῦμε νὰ θεωρήσουμε ὅτι κινεῖται μὲ μικρότερη ταχύτητα, γιατὶ τὰ τελικὰ συμπεράσματα δὲν ἀλλοιώνονται.
Ταυτόχρονα θὰ ἐκτελεῖ κυκλικὴ τροχιὰ γύρω ἀπὸ τὸν Ἥλιο, εὑρισκόμενος πάντα στὸ ἴδιο ἐπίπεδο τῶν οὐράνιων σωμάτων τοῦ πειράματος. Δηλαδὴ καὶ ὁ φανταστικὸς μετρητὴς μεγάλων ἀποστάσεων καὶ ὁ παρατηρητὴς A θὰ κινοῦνται ταυτόχρονα καὶ μὲ τὴν ἴδια γραμμικὴ ταχύτητα υΔ (σὲ μέτρο, διεύθυνση καὶ φορὰ) ποὺ κινεῖται καὶ ὁ Ἥλιος, λόγω τῆς διαστολῆς τοῦ Σύμπαντος. Ἔτσι, ὁ παρατηρητὴς A θὰ ἀντιληφθεῖ μία ἀπολύτως κυκλικὴ τροχιά, τὴ διάρκεια τῆς ὁποίας θὰ μετρήσει.
Καταρχήν, θεωροῦμε ὅτι ἡ διαστολὴ τοῦ σύμπαντος εἶναι σφαιρικὴ μὲ κέντρο του τὸ σημεῖο τῆς μεγάλης ἔκρηξης. Εἶναι μιὰ θεώρηση ποὺ στὴ συνέχεια, μὲ τὴν παρουσίαση τοῦ συμπαντικοῦ μοντέλου ποὺ στηρίζεται στὴν Τετρακτύν, θὰ ἀνατραπεῖ.
Ἔστω ὅτι ὑπάρχει καὶ ἕνας δεύτερος παρατηρητὴς Β, ὁ ὁποῖος, τὴν χρονικὴ στιγμὴ ποὺ ξεκινάει τὸ πείραμα, βρίσκεται στὴν ἴδια θέση μὲ αὐτὴν τοῦ παρατηρητῆ A, μὲ μία διαφορὰ ὅμως. Ὁ παρατηρητὴς Β εἶναι «δεμένος» μὲ τὸ σημεῖο τῆς Μεγάλης Ἔκρηξης καὶ ἑπομένως παραμένει ἀκίνητος. Ὁ παρατηρητὴς Β θὰ ἀντιλαμβάνονταν τὸν μετρητὴ μεγάλων ἀποστάσεων νὰ κάνει μιὰ σπειροειδὴ τροχιὰ καὶ νὰ καταλήγει στὴ νέα θέση τοῦ παρατηρητὴ Α.
Μὲ δεδομένο ὅτι ὁ μετρητὴς μεγάλων ἀποστάσεων θεωρητικὰ κινεῖται πάνω σὲ κύλινδρο, οἱ δύο διαφορετικὲς μετρήσεις θὰ μποροῦσαν νὰ ἀναχθοῦν σὲ πλευρὲς ὀρθογωνίου τριγώνου, μὲ ὑποτείνουσα ἴση μὲ τὴ μέτρηση τοῦ παρατηρητὴ Β (μΒ) καὶ μὲ μία κάθετη πλευρὰ ἴση μὲ τὴ μέτρηση τοῦ παρατηρητὴ Α (μΑ). Ἡ ἄλλη κάθετη πλευρὰ θὰ ἔδινε τὴν ἀπομάκρυνση τοῦ συστήματος ἀπὸ τὸ σημεῖο τῆς Μεγάλης Ἔκρηξης ΒΒ, γιὰ ὅλη τὴ διάρκεια τοῦ πειράματος.
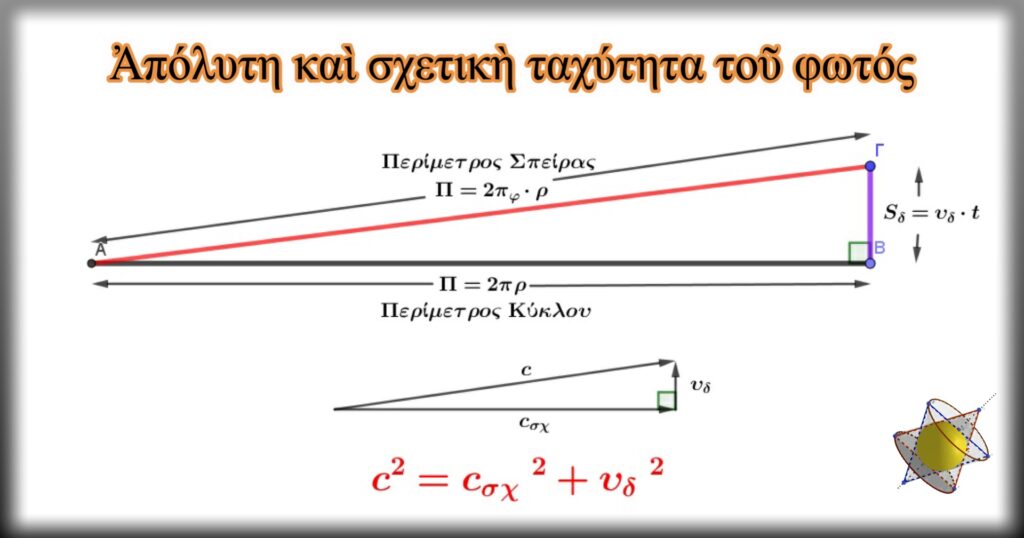
Ὁ παρατηρητὴς Β γνωρίζει τὴν πραγματικὴ ταχύτητα τοῦ φωτὸς c, ὅπως καὶ τὴν τιμὴ τοῦ ἀριθμοῦ πφ , ἡ ὁποία ἐμπεριέχει καὶ τὴν τέταρτη διάσταση τοῦ χρόνου.
Ὁ παρατηρητὴς Α γνωρίζει τὴν κάθετη συνιστώσα τῆς ταχύτητας τοῦ φωτὸς cσχ ὡς πρὸς ἀκτινικὴ διεύθυνση διαστολῆς τοῦ σύμπαντος, γιατὶ αὐτὴ τοῦ εἶναι ἀντιληπτή. Αὐτὴν τὴν ταχύτητα ἔχει μετρήσει στὰ 299.792,465km/sec. Ἐπίσης τοῦ εἶναι γνωστὴ ἡ τιμὴ τοῦ ἀριθμοῦ π, ὅπως τὴν ὑπολόγισε μὲ προσεγγιστικές μεθόδους στὸν τρισδιάστατο χῶρο μέσα στὸν ὁποῖο κινεῖται καὶ οἱ αἰσθήσεις τοῦ ἐπιτρέπουν νὰ ἀντιληφθεῖ ἄμεσα.
Θεωροῦμε ὅτι ἡ διαστολὴ τοῦ Σύμπαντος ἀποτελεῖ τὸ μέγιστο φυσικὸ ἐξελικτικὸ φαινόμενο ποὺ μπορεῖ νὰ περιγραφθεῖ μὲ ἀκολουθία τῆς μορφῆς Φν=α·φν. Ἔτσι, γιὰ Κανονικὲς Συνθῆκες στὶς ὁποῖες ἀναφέρεται ἡ ἀκολουθία καὶ γιὰ Κανονικὲς Συνθῆκες ποὺ ἐπικρατοῦν στὸ σημεῖο τοῦ Σύμπαντος ὅπου ἔγιναν οἱ μετρήσεις, ὁ λόγος c/cσχ θὰ εἶναι σταθερός. Ὅπως εἴδαμε, γιὰ Κανονικὲς Συνθῆκες καὶ γιὰ τὴν ἀκολουθία Δ=δ·φν, ὁ ἀντίστοιχος λόγος ποὺ προέκυψε πφ/π, εἶναι σταθερός. Ἐπειδὴ καὶ οἱ δύο ἀκολουθίες κινοῦνται στὸν ἴδιο χωροχρόνο καὶ μὲ ἀνάλογους κανόνες, περιμένουμε, καταρχὴν θεωρητικὰ νὰ ἰσχύει ἡ σχέση:
Ἔστω ὅτι μὲ βάση αὐτὸν τὸν τύπο, ὁ Παρατηρητὴς Β ἔχει ὑπολογίσει τὴν ἀπόλυτη ταχύτητα τοῦ φωτὸς ποὺ θὰ εἶναι: c=299.797,0515km/sec. Τὰ δεδομένα αὐτὰ θὰ τύχουν βελτιώσεων στὴ συνέχεια.
Θὰ θεωρήσουμε ὅτι καὶ γιὰ τὸν παρατηρητὴ Β, ὁ χρόνος τοῦ πειράματος κυλάει τὸ ἴδιο στὸ συγκεκριμένο σημεῖο τοῦ Σύμπαντος ὅπως καὶ γιὰ τὸν παρατηρητὴ A, ἢ ὀρθότερα ὅτι ὁ παρατηρητὴς Β χρησιμοποιεῖ τὴν ἴδια μονάδα μέτρησης χρόνου μὲ τὸν παρατηρητὴ A. Οἱ μετρήσεις τους ὅμως εἶναι διαφορετικές. Αὐτὲς δίνονται στὸν ἑπόμενο πίνακα.
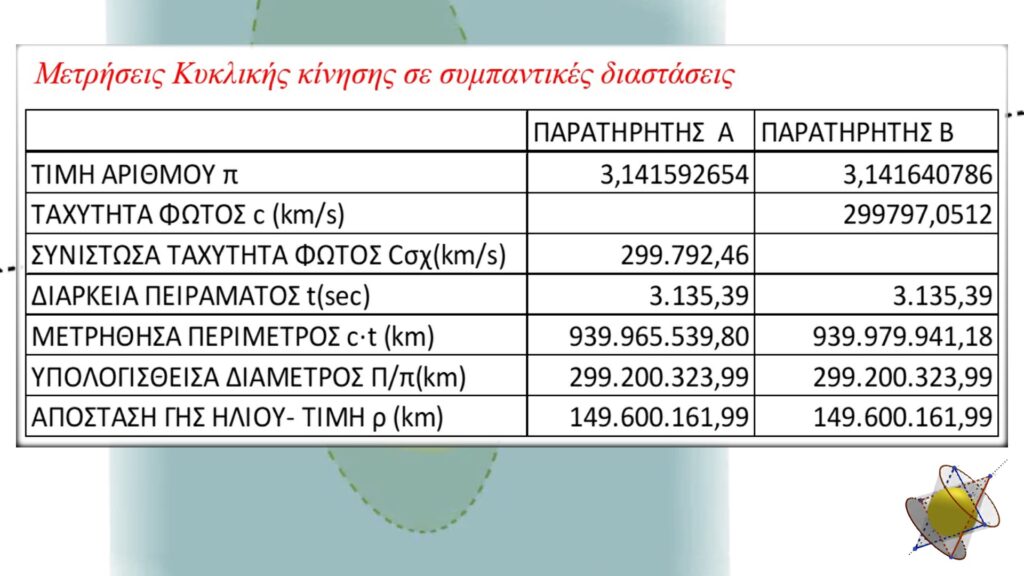
Τὰ ἀποτελέσματα τοῦ παρατηρητὴ Α εἶναι ἀπολύτως ὀρθὰ γιὰ τὸν ἴδιο, γιατὶ δὲν γνωρίζει, ἢ δὲν λαμβάνει ὑπόψη του, λόγῳ τῆς σχετικότητας, τὴ διαφορὰ μεταξὺ τῆς ἀπόλυτης ταχύτητας τοῦ φωτὸς c καὶ τῆς συνιστώσας, σχετικῆς ταχύτητας τοῦ φωτὸς cσχ.
Ὁ παρατηρητὴς Β τὸ γνωρίζει καὶ ξέρει ὅτι γιὰ νὰ ταυτισθοῦν οἱ μετρήσεις τῆς περιμέτρου, πρέπει νὰ ψαλιδίσει τὴ διαφορὰ τους, ἀφαιρώντας τὴν ἐπίδραση τῆς διαστολῆς τοῦ Σύμπαντος, δηλαδὴ τὴν ἐπίδραση τῆς ταχύτητας κίνησης τῶν οὐράνιων σωμάτων, δηλαδὴ τῆς ἐπίδρασης τοῦ χρόνου σὰν διάσταση.
Αὐτὸ κάναμε καὶ ἐμεῖς προηγουμένως στὸν ὑπολογισμὸ τοῦ ἀριθμοῦ π μέσω τῆς ἀκολουθίας Δ. Στὴν πράξη, θέλαμε καὶ τελικὰ ἀφαιρέσαμε σὲ πολὺ μεγάλο βαθμὸ τὴν ἐπίδραση τοῦ χρόνου ὅπως αὐτὸς ὑπεισέρχονταν στὴν τιμὴ του.
Ἔχουμε λοιπὸν τὴν τιμὴ πφ=6/5·φ2, ποὺ ἰσχύει γιὰ συμπαντικὲς ἐφαρμογές, ὅπου ἐμπεριέχεται καὶ ἡ ἐπίδραση τῆς τέταρτης διάστασης, δηλαδὴ τοῦ χρόνου. Ἔχουμε καὶ τὴν ἰσχύουσα τιμὴ τοῦ ἀριθμοῦ π γιὰ εὐκλείδειες, τρισδιάστατες ἐφαρμογές, ἀπαλλαγμένη ἀπὸ αὐτὴν τὴν παράμετρο.
Μὲ βάση αὐτὸ τὸ μοντέλο, καὶ μὲ χρήση τοῦ προηγούμενου ὀρθογώνιου τρίγωνο τοῦ πειράματός μας, θὰ μπορούσαμε νὰ ὑπολογίσουμε τὴν ἐλάχιστη ταχύτητα κίνησης τῶν οὐράνιων σωμάτων, σὲ σχέση μὲ τὸ ἀκίνητο σημεῖο τῆς Μεγάλης Ἔκρηξης, δηλαδὴ τὴν ταχύτητα διαστολῆς τοῦ Σύμπαντος. Αὐτὴ θὰ ὑπολογίζονταν στὰ 1.659,5238km/sec. Ἐπίσης, θὰ μποροῦσε τὸ μοντέλο αὐτὸ νὰ δικαιολογήσει τὶς διαφαινόμενες μεταβολὲς στὴν τιμὴ τῆς παραπάνω ταχύτητας καὶ ἑπομένως καὶ τὸν ρυθμὸ μεταβολῆς τῆς διαστολῆς τοῦ Σύμπαντος. Συνήθως μετροῦνται ταχύτητες ἀπομάκρυνσης οὐράνιων σωμάτων σὲ σχέση μὲ κοντινοὺς Γαλαξίες, ἀλλὰ καὶ αὐτοὶ ἔχουν σχετικὲς ταχύτητες κίνησης λόγῳ τῶν ἐλλειπτικῶν τροχιῶν ποὺ διαγράφουν. Ἔτσι, μποροῦν καὶ περνοῦν ἀπὸ φάσεις τῆς ἐλλειπτικῆς τροχιὰς ποὺ σχετικώς πλησιάζουν πρὸς τὸ σημεῖο ΒΒ, ὁπότε φαινομενικὰ καὶ περιοδικά ἡ συνισταμένη ταχύτητα ἀπομάκρυνσης μειώνεται, ἐνῶ στὴν ἀντίθετη φάση ἡ συνισταμένη ταχύτητα αὐξάνεται. Οἱ μεταβολὲς αὐτὲς ὅμως εἶναι πολὺ μικρές. Ὅπως θὰ φανεῖ σὲ ἑπόμενες σελίδες, ὑπάρχουν πολὺ σημαντικώτεροι λόγοι ποὺ δικαιολογοῦν τὶς μεταβολὲς τῆς ταχύτητας διαστολῆς τοῦ Σύμπαντος καὶ ἑπομένως καὶ τῆς ταχύτητας τοῦ φωτὸς ποὺ μᾶς γίνεται ἀντιληπτή.
Σχέση ταχύτητας του φωτὸς καὶ χρόνου
Ὅλα τὰ φυσικὰ ἐξελικτικὰ φαινόμενα ἔχουν ἀρχὴ καὶ τέλος, δηλαδὴ ἔχουν συγκεκριμένη διάρκεια, συγκεκριμένο χρόνο. Αὐτὸς παραστατικὰ καὶ διαχρονικὰ μπορεῖ νὰ ἀποδοθεῖ καὶ μὲ τοὺς κόκκους ἄμμου ποὺ ρέουν σὲ μία κλεψύδρα. Τὸ ἄνοιγμα τῆς κλεψύδρας στὸ μέσον της καθορίζει καὶ τὴ ροὴ τοῦ χρόνου.
Στο Σύμπαν, ἡ συνισταμένη ταχύτητα κίνηση ἑνὸς συστήματος, θὰ καθορίζει καὶ τὴν ροὴ τοῦ χρόνου, ἡ ὁποία σὲ αὐτὸ τὸ ἐπίπεδο δὲν εἶναι θεμελιῶδες μέγεθος, ἀλλὰ παράγωγο. Θὰ πρέπει νὰ δίνεται ἀπὸ μία ἐξίσωση τῆς γενικώτερης μορφῆς ΔPt=f(α)·cσχ/υΔ. Ἡ παράμετρος f(α) θὰ καθορίζει τὴ μονάδα μέτρησης τοῦ χρόνου. Ἡ ἀπόλυτη ταχύτητα τοῦ φωτὸς εἶναι θεμελιῶδες μέγεθος καὶ μπορεῖ νὰ παίξει τὸν ρόλο παγκόσμιας συμπαντικῆς σταθεράς. Κάθε φορὰ θὰ ἀποτελεῖ τὴν σταθερὴ σὲ μέτρο, διαγώνιο ὀρθογωνίου παραλληλογράμμου, μὲ κάθετες πλευρὲς τὶς ἑκάστοτε τιμὲς τῆς συνισταμένης ταχύτητας κίνησης τοῦ συστήματος υΔ, καὶ τῆς ἀντίστοιχης κάθετης συνιστώσας τῆς σχετικῆς ταχύτητας τοῦ φωτὸς cσχ. Οἱ τιμὲς τους συνδέονται μεταξὺ τοὺς μὲ μιὰ πολὺ σημαντικὴ σχέση, ἀπόρροια τοῦ πυθαγορείου θεωρήματος:
c2=cσχ2+υΔ2
Ἔτσι, ἐὰν φτάναμε σὲ σημεῖο ὅπου ἀναπτύσσονται ἀπίστευτα ἰσχυρὲς βαρυτικές δυνάμεις (Μαῦρες Τρύπες), τότε ἡ συνισταμένη ταχύτητα κίνησης τοῦ συστήματος θὰ πλησίαζε τὴν ταχύτητα τοῦ φωτός. Ἡ ἀντίστοιχη κάθετη συνιστώσα ταχύτητα τοῦ φωτὸς cσχ, ποὺ ὁ παρατηρητὴς Α ἀντιλαμβάνεται λανθασμένα σὰν πραγματικὴ ταχύτητα τοῦ φωτὸς c, θὰ μειώνονταν δραστικὰ καὶ ἡ γωνία ω θὰ ἔφτανε ὁριακὰ στὴν τιμὴ μηδέν, ὅπως καὶ ἡ ἀντίστοιχη τιμὴ τῆς ἐφαπτομένης ω (εφω=cσχ/υΔ). Ἔτσι, ὁ χρόνος θὰ περνοῦσε πολὺ ἀργὰ γιὰ νὰ φτάσουμε στὴν ἀκραία κατάσταση ὅπου, ὅταν ἡ ταχύτητα τοῦ παρατηρητὴ Α θὰ ἔφτανε τὴν ταχύτητα τοῦ φωτός, ἡ στρόφιγγα τῆς κλεψύδρας θὰ ἔκλεινε καὶ ὁ χρόνος θὰ σταματοῦσε (αἰώνια ζωή).
Στὴν ἀντίθετη ὁριακὴ κατάσταση ὅπου ἡ διαστολὴ τοῦ Σύμπαντος θὰ σταματοῦσε, τότε ἡ συνιστώσα cσχ θὰ ἄγγιζε τὴν τιμὴ τῆς ταχύτητας τοῦ φωτὸς c, ἡ γωνία ω θὰ γίνονταν ὀρθή, μὲ τιμὴ ἐφαπτομένης νὰ τείνει στὸ ἄπειρο. Ἔτσι, ὁ χρόνος θὰ ἔτρεχε μὲ ἄπειρη ταχύτητα καὶ θὰ ἐξαντλοῦνταν ἀκαριαία, ἐπιφέροντας τὸν στιγμιαῖο θάνατο.
Θεμελιώδης Συμπαντικός Λόγος
Ἐπιστρέφουμε στὴν ἐξίσωση
Σὲ αὐτὴ θὰ πρέπει νὰ δεχθοῦμε ὅτι οἱ λόγοι προκύπτουν ἀπὸ δύο πολὺ συγκεκριμένες καταστάσεις κίνησης τῆς ὕλης. Ἡ τιμὴ πφ θὰ εἶναι συνδεδεμένη μὲ τὴν ταχύτητα κίνησης τῆς ὕλης ὅταν αὐτὴ τείνει πρὸς τὴν ἐλάχιστη ἐπιτρεπτή, αὐτὴ ποὺ ἐνδεχομένως ὁ Ἡράκλειτος θεώρησε σὰν τὴν ἐλάχιστη ἀπαραίτητη γιὰ νὰ ὑπάρχει κίνηση στὸ Σύμπαν καὶ ἑπομένως Ζωή. Μὲ τὴ σειρὰ της, ἡ ἐλάχιστη ἐπιτρεπτὴ ταχύτητα διαστολῆς τοῦ Σύμπαντος θὰ δώσει καὶ τὴ μέγιστη σχετικὴ ταχύτητα τοῦ φωτὸς cσχ(max) ἡ ὁποία θὰ ἔχει τιμὴ πολὺ κοντὰ στὴν ἀπόλυτη ταχύτητα τοῦ φωτός. Ἡ γνωστὴ τιμὴ π θὰ πρέπει νὰ σχετίζεται μὲ μιὰ ταχύτητα διαστολῆς τοῦ Σύμπαντος ὅπου πλέον ὁ παράγοντας χρόνος δὲν θὰ ἔχει ἐπίδραση στὶς μετρήσεις. Αὐτὴ ἡ ταχύτητα θεωροῦμε ὅτι εἶναι ἡ μηδενικὴ ταχύτητα διαστολῆς, ὅπου, ὅπως εἰκάσαμε, ὁ χρόνος ἀκαριαία ἐξαντλεῖται, ἑπομένως δὲν ὑφίσταται σὰν παράμετρος καὶ ἑπομένως δὲν ἐπιδρᾶ. Εἶναι ὁ ἀριθμὸς π ὅπως τὸν γνωρίσαμε καὶ τὸν ὑπολογίσαμε στὸν τρισδιάστατο εὐκλείδειο χῶρο.
Ὁ συγκεκριμένος λόγος, ἐφόσον εὐσταθεῖ, φαίνεται νὰ εἶναι σημαντικώτατος γιὰ τὴ δομὴ τοῦ Σύμπαντος, γιὰ αὐτὸ θὰ τὸν ἀποκαλέσουμε Θεμελιώδη Συμπαντικό Λόγο. Γιά νὰ ἰσχύει ὅμως πρέπει καὶ νὰ άποδεικνύεται. Τὴν ἀπόδειξη θὰ τὴν δοῦμε στὴν παρουσίαση τοῦ συμπαντικοῦ μοντέλου τῆς Τετρακτύος, ἡ ὁποία εἶναι ἀπλὰ ἀποκαλυπτική. Πρίν ὅμως πρέπει νὰ ἀποκωδικοποιήσουμε τὴν Τετρακτύν.

