Ὁ τετραγωνισμὸς τοῦ κύκλου στὸ Πὶ καὶ Φί
Κυβισμὸς μοναδιαίας σφαίρας
Ἀπό τὸ βιβλίο…

Ἡ περεταίρω ἔρευνα τοῦ γεωμετρικοῦ μηχανισμοῦ ἔδωσε μιὰ πολὺ ἐνδιαφέρουσα κατασκευή.
Ὅπως εἶναι γνωστὸ ὁ ὄγκος τῆς σφαίρας δίνεται ἀπὸ τὸν τύπο: V=4/3·πr³
Γιὰ νὰ μπορέσουμε νὰ κατασκευάσουμε κύβο μὲ τὸν ἴδιο ὄγκο (V=α³) ἀρκεῖ νὰ κατασκευάσουμε τὴν ἀκμὴ του α, ἴση μὲ τὴν τρίτη ρίζα τοῦ ὄγκου τῆς σφαίρας. Μπορεῖ ὅμως κάτι τέτοιο νὰ ἐπιτευχθεῖ; Ἐὰν ναὶ, τότε θὰ λύναμε τὸ δεύτερο «ἄλυτο» πρόβλημα ποὺ οἱ ἀρχαῖοι σοφοὶ, γιὰ κάποιον ἀνώτερο λόγο ἔθεσαν, τὸ «δήλιο πρόβλημα».
Ἂς δοῦμε ὅμως τί μᾶς ἐπιφυλάσσει ὁ μηχανισμός.
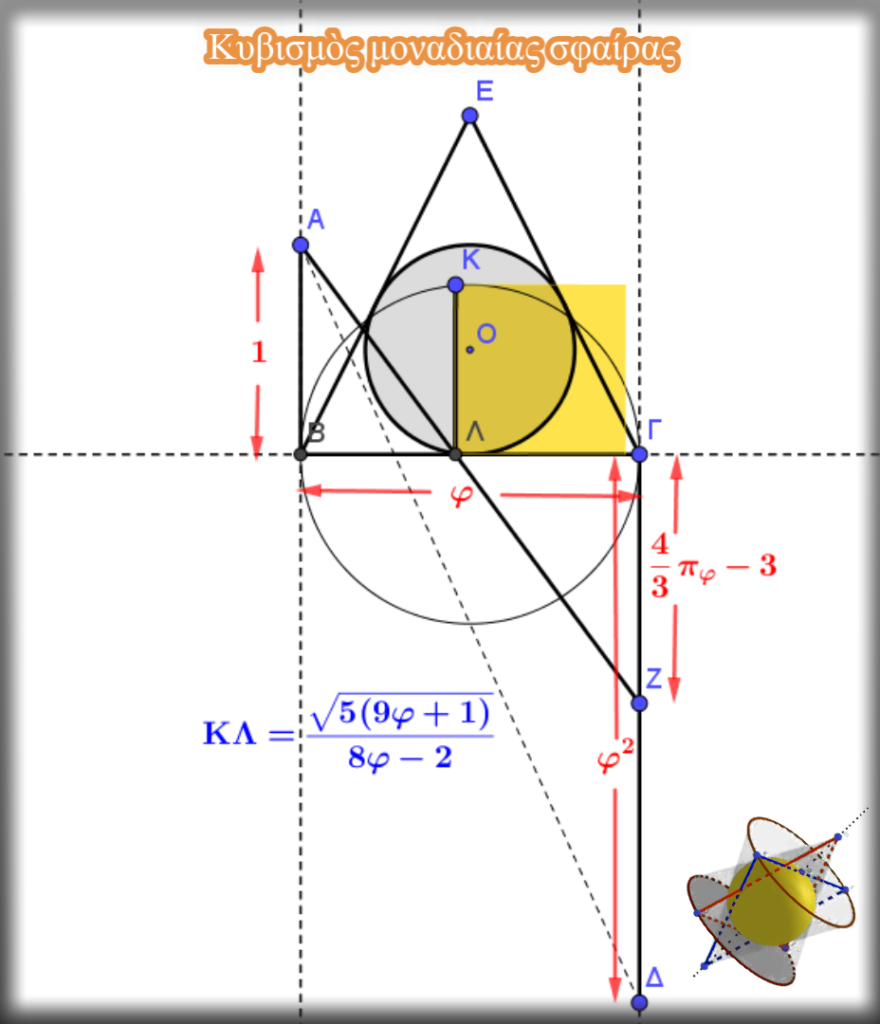
Κατασκευή
Στὴν ἴδια μαιανδρική διάταξη ποὺ μᾶς ἔδωσε τὸν ἀριθμὸ πφ καὶ ποὺ μὲ βάση αὐτὸν μᾶς τετραγώνισε τὸν κύκλο, παίρνουμε τὸ εὐθύγραμμο τμῆμα ΓΖ=4/3·π-3. Τὸ συγκεκριμένο εὐθύγραμμο τμῆμα μπορεῖ νὰ κατασκευαστεῖ μὲ διάφορους τρόπους. Ἕνας πολὺ ἐνδιαφέρον τρόπος ἀναφέρεται στὸ βιβλίο μου «γεωμετρικὲς κατασκευὲς στὸ Πὶ καὶ Φί». Ἐπίσης ἐνδιαφέρον ἔχει ἡ ἐμφάνιση τοῦ λόγου 4/3·π, τὸν ὁποῖο συναντοῦμε καὶ στὸν τύπο ποὺ μᾶς δίνει τὸν ὄγκο σφαίρας.
Φέρνουμε τὸ ΑΖ εὐθύγραμμο τμῆμα ποὺ τέμνει τὸ ΒΓ στὸ σημεῖο Λ.
Κάθετη εὐθεία στὸ ΒΓ ἀπὸ τὸ σημεῖο Λ τέμνει τὸν κύκλο μὲ διάμετρο ΒΓ στὸ σημεῖο Κ.
Τὸ εὐθύγραμμο τμῆμα ΚΛ ὑπολογίστηκε καὶ βρέθηκε ὅτι εἶναι : 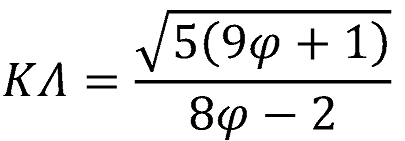
μὲ τιμὴ ΚΛ= 0,80600011077052647…
Ἡ τιμὴ τῆς τρίτης ρίζας τοῦ ὄγκου τῆς μοναδιαίας σφαίρας μὲ διάμετρο ΑΒ=1 ἐὰν θεωρήσουμε ἀποδεκτὴ τὴν τιμὴ πφ εἶναι: 0,80600009325733…
ἐνῶ ἡ ἀντίστοιχη τιμὴ μὲ τὴν χρήση τῆς ἰσχύουσας τιμῆς τοῦ ἀριθμοῦ π εἶναι: 0,805995977008235…
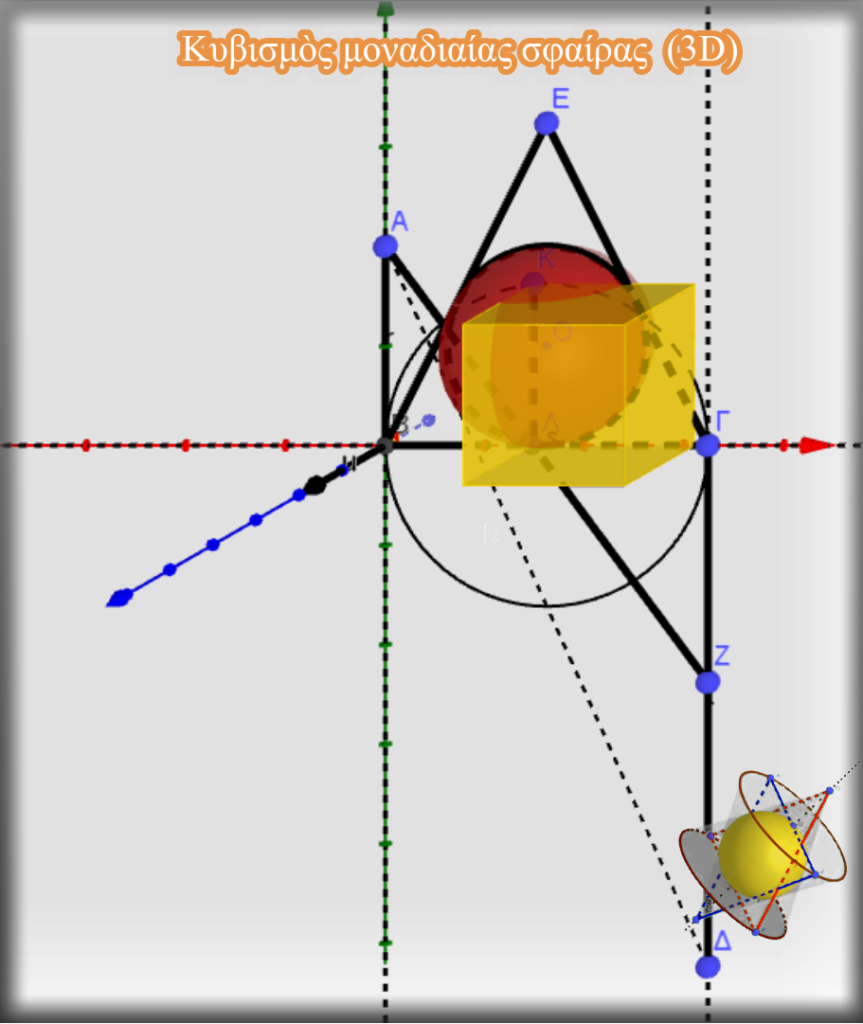
Φυσικά, ἡ συγκεκριμένη γεωμετρικὴ κατασκευὴ κύβου ἴσου ὄγκου μὲ δοσμένη σφαίρα, θεωρεῖται καὶ εἶναι προσεγγιστική. Ἡ ἀπόκλιση τῶν δύο τιμῶν εἶναι τῆς ἰδίας τάξης μεγέθους μὲ αὐτῆς τοῦ τετραγωνισμοῦ τοῦ κύκλου (λ=1,000015321…). Αὐτό, μᾶς ἐπιτρέπει νὰ ὑποθέσουμε πώς καὶ οἱ δύο γεωμετρικὲς κατασκευὲς ἔχουν κοινὴ ἀφετηρία καὶ λογική, κυρίως ὅμως μᾶς ὑποδεικνύει πώς ἡ ἀπόκλιση τῶν τιμῶν δὲν εἶναι τυχαία. Σὲ αὐτὴν κρύβονται γνώσεις ποὺ ὅταν μᾶς ἀποκαλυφθοῦν θὰ δώσουν ἀπαντήσεις ἱκανὲς νὰ ἀλλάξουν τὴν ἄποψη ποὺ ἔχουμε άκόμη καὶ γιὰ τὴν δομὴ καὶ τὴν λειτουργία τοῦ Σύμπαντος μας. Γιὰ νὰ φτάσουμε ὅμως ἐκεῖ, χρειάζονται, πέρα τῶν ὑπαρχόντων, νέες γνώσεις καὶ ἐργαλεῖα, ποὺ στὴ συνέχεια τῶν σελίδων θὰ ἀποκομίσουμε.

