Ἡ μελοποιημένη ἀρχαία ἑλληνικὴ ποίηση
Σειρὰ Fibonacci καὶ τριγωνικοὶ ρυθμοί
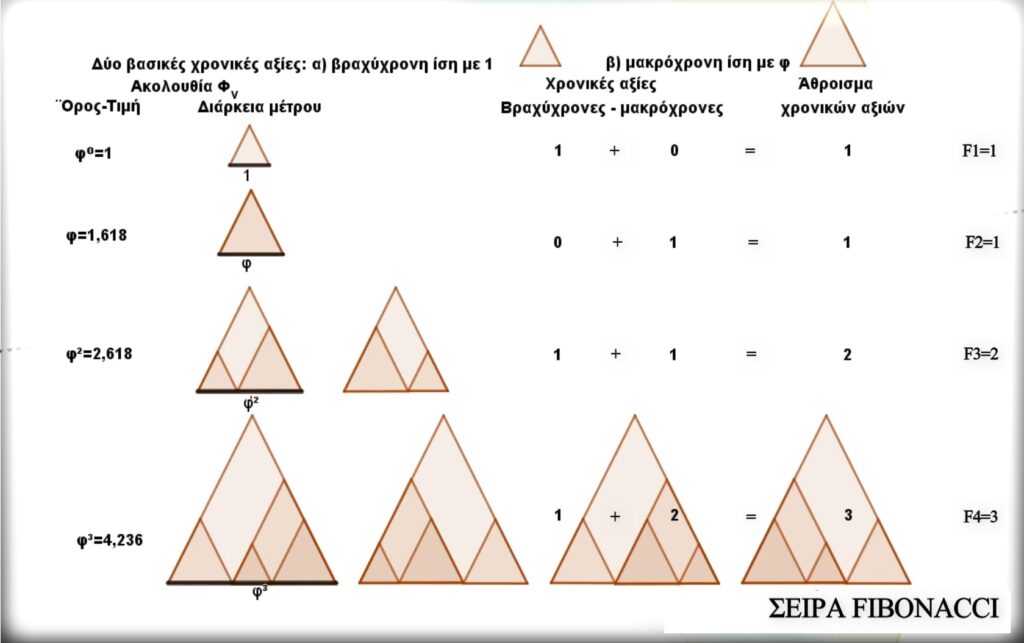
Ὅπως ἔχουμε ἤδη ἀναφέρει, στοὺς κατὰ φ μουσικοὺς ρυθμοὺς ὑπάρχουν δύο βασικὲς χρονικὲς ἀξίες. Ἐὰν ἡ διάρκεια τῆς βραχύχρονης θεωρηθῆ ἴση μὲ 1, τότε αὐτὴ τῆς μακρόχρονης θὰ εἶναι ἴση μὲ φ (1,618…)
Θὰ ἀντιμετωπἰσουμε τὴν δημιουργία τῶν μουσικῶν ρυθμῶν σὰν ἕνα φυσικὸ ἐξελικτικό φαινόμενο, ὅπου ἡ διάρκεια τοῦ μέτρου θὰ εἶναι αύτὴ ποὺ κάθε φορὰ θὰ αὐξάνεται κατὰ φ φορές.
Ζητούμενο εἶναι ἡ διάρκεια τοῦ κάθε νέου μέτρου ποὺ θὰ προκύπτη, νὰ μπορεῖ νὰ καλυφτῆ ΕΠΑΚΡΙΒΩΣ μὲ συνδυασμὸ βραχύχρονων καὶ μακρόχρονων ἀξιῶν.
Ὁ κάθε ἑπόμενος ὄρος τῆς ἀκολουθίας φ θὰ καθορίζη καὶ μία νέα ὁμάδα μουσικῶν ρυθμῶν μὲ διάρκεια μέτρου ἴση μὲ τὴν τιμὴ τοῦ ἀντίστοιχου ὅρου.

Ὁ πρῶτος ὄρος τῆς ἀκολουθίας φ θὰ μᾶς δώσει καὶ τὴν πρώτη ὁμάδα μουσικῶν ρυθμῶν μὲ διάρκεια μέτρου ἴση μὲ τὴν τιμὴ τοῦ ἀντίστοιχου ὄρου, ἴση μὲ 1. Ἡ διάρκεια ὅμως αὐτοῦ τοῦ μέτρου καλύπτεται ἐπακριβῶς μὲ τὴν χρήση μίας καὶ μόνο χρονικῆς ἀξίας, τῆς βραχύχρονης. Εἶναι ἡ ὁμάδα μὲ τοὺς πιὸ ἀπλοὺς μουσικοὺς ρυθμοὺς. Στὴν ὁμάδα αὐτὴ ἀνήκει τὸ σύνολο σχεδόν τῶν μουσικῶν ρυθμῶν τοῦ σύγχρονου δυτικοευρωπαϊκοῦ μας πολιτισμοῦ ποὺ ἐπιλέξαμε νὰ ἀκολουθήσουμε, ἀποδεικνύοντας παράλληλα ὅτι αὐτὰ ποὺ σήμερα γνωρίζουμε καὶ χρησιμοποιοῦμε στὴ μουσικὴ δὲν εἶναι ξέχωρα μὲ ὅσα ἐδῶ παρουσιάζονται, ἁπλὰ ἀποτελοῦν ἕνα πολὺ μικρὸ ὑποσύνολο ἑνὸς τεράστιου μουσικοῦ κόσμου ποὺ ἀνοίγεται μπροστὰ μας. Τοὺς ρυθμοὺς αὐτοὺς θὰ τοὺς ὀνομάσουμε βραχύχρονους βηματικούς.
Ἡ τιμὴ τοῦ δεύτερου ὅρου τῆς ἀκολουθίας φ θὰ μᾶς δώσει καὶ τὴν δεύτερη ὁμάδα μουσικῶν ρυθμῶν, αὐτῶν μὲ διάρκεια μέτρου ἴση μὲ φ, ἴση μὲ 1,618. Ἡ διάρκεια καὶ αὐτοῦ τοῦ μέτρου μπορεῖ νὰ καλυφτῆ μὲ τὴν χρήση μίας καὶ μόνο χρονικῆς ἀξίας, αὐτὴν τὴν φορά ὅμως τῆς μακρόχρονης. Δηλαδὴ καὶ πάλι στὴν πραγματικότητα ἔχουμε βηματικοὺς ρυθμοὺς. Αὐτοὺς θὰ τοὺς ὀνομάσουμε μακρόχρονους βηματικοὺς.
Ἀπό τὸ σημεῖο αὐτὸ ξεκινᾶ τὸ σημαντικότερο μέρος τῆς δημιουργίας τῶν μουσικῶν ρυθμῶν.
Ἐὰν προσθέσουμε τὰ δύο προηγούμενα μέτρα, δηλαδὴ τὸ μακρόχρονο βηματικὸ καὶ τὸ βραχύχρονο βηματικό, τότε θὰ προκύπτει ἕνα νέο μέτρο μὲ διάρκεια ἴση μὲ 2,618. Αὐτὴ ὅμως εἶναι ἡ τιμὴ τοῦ τρίτου ὅρου τῆς ἀκολουθίας φ, ἡ τιμὴ φ². Εἶναι ὁ ρυθμὸς ποὺ τὸ μέτρο του συμπληρώνεται ἐπακριβῶς μὲ μία βραχύχρονη καὶ μιὰ μακρόχρονη ἀξία. Εἶναι ὁ πιὸ ἁπλὸς κατὰ φ μουσικός ρυθμός. Ἡ διαφορετικὴ σειρὰ μὲ τὴν ὁποία θὰ ἐμφανίζονται ἡ μακρόχρονη καὶ ἡ βραχύχρονη ἀξία, κάθε φορὰ θᾶ μᾶς δίνει καὶ διαφορετικὴ παραλλαγὴ τοῦ ρυθμοῦ. Τοὺς ρυθμοὺς αὐτῆς τῆς ὁμάδας θὰ τοὺς ὀνομάσουμε τριγωνικοὺς δυάρι.

Γενικότερα τοὺς ρυθμοὺς τῆς κατηγορἰας, θὰ τοὺς ὀνομάζουμε τριγωνικοὺς καὶ θὰ τοὺς ἀποτυπώνουμε μὲ ἕνα χρυσὸ τρίγωνο, μέσα στο ὁποῖο θὰ ἐμφανίζονται μικρότερα χρυσὰ τρίγωνα, καὶ γιὰ νὰ τονίσουμε τὴν σημασία τῆς χρυσῆς τομῆς στὴν δημιουργία τους, ἀλλὰ καὶ γιὰ νὰ ἀποδόσουμε ὅσο γίνεται παραστατικότερα τὴν μορφὴ αύτῶν, καθῶς καὶ τὴν σειρὰ μὲ τὴν ὁποία θὰ ἐμφανίζονται οἱ μακρόχρονες καὶ οἱ βραχύχρονες ἀξίες στὸ μέτρο.
Ἐὰν τώρα προσθέσουμε τὸν τριγωνικὸ δυάρι ρυθμὸ μὲ τὸν μακρόχρονο βηματικό, τότε θὰ προκύψει ἡ ἑπόμενη ὁμάδα μουσικῶν ρυθμῶν μὲ τιμὴ μέτρου ἴση μὲ φ³, ἴση μὲ 4,236. Αὐτὴ ἡ διάρκεια μέτρου καλύπτεται αὐστηρὰ μὲ τὴν χρήση δύο μακρόχρονων καὶ μίας βραχύχρονης ἀξίας (ἄθροισμα τῶν δύο προηγούμενων ρυθμῶν). Ἡ διαφορετικὴ σειρὰ πρόσθεσης τῶν ἐπιμέρους ρυθμῶν, καθῶς καὶ ἡ διαφερετικὴ μορφὴ τους, κάθε φορά θὰ μᾶς δίνη και μία διαφορετικὴ παραλλαγὴ τοῦ ρυθμοῦ, μόνο ποὺ ἐδῶ οἱ ἐπιλογές μας σαφῶς καὶ θὰ εἶναι περισσότερες. Τοὺς ρυθμοὺς αὐτῆς τῆς ὁμάδας θὰ τοὺς ὀνομάσουμε τριγωνικοὺς τριάρι.

Τὸ ἄθροισμα τῶν βραχύχρονων καὶ μακρόχρονων ἀξιῶν τοῦ κάθε μέτρου, κάθε φορὰ θὰ μᾶς δίνει τὴν τιμὴ τοῦ ἀντίστοιχου ὄρου τῆς σειρὰς Fibonacci, ἀποκαλύπτοντας μας ἔτσι καὶ τὴ μεταξύ τους μουσικὴ σχέση. Γιὰ αὐτὸ τὸ λόγο, τοὺς ρυθμοὺς τῆς κατηγορίας θὰ τοὺς ὀνομάσουμε καὶ ρυθμοὺς Fibonacci, τονίζοντας ἔτσι τὴ σημασία τῆς σειρᾶς στὴν δημιουργία τους.
Συγκεντρωτικά, τὶς πρῶτες ὁμάδες τριγωνικῶν ρυθμῶν τὶς βλέπουμε στὸν ἐπόμενο πίνακα.
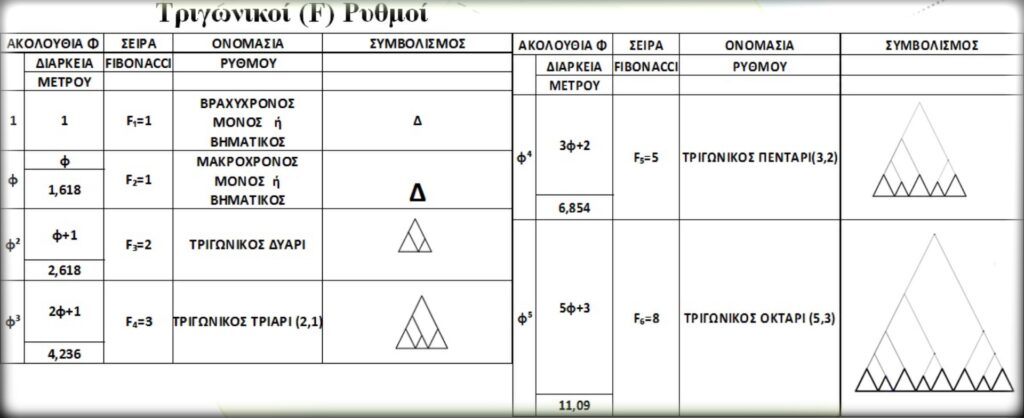
Εἶναι σημαντικό νὰ έπαναλάβω ὅτι ἀντιμετωπίσαμε τὴ δημιουργία τῶν μουσικῶν ρυθμῶν σὰν νὰ πρόκειται γιὰ ἕνα φυσικὸ ἐξελικτικὸ φαινόμενο ὅπου γιὰ νὰ ἐμφανιστῆ ὁ ἐπόμενος ρυθμὸς θὰ πρέπει ἤδη να ὑπάρχουν οἱ προηγούμενοι. Αὐτὸ εἶναι ἀπαραίτητο διότι στὴν πραγματικότητα οἱ ρυθμοὶ ποὺ προκύπτουν εἶναι ὅλοι σύνθετοι, εἶναι ἀποτέλεσμα σύνθεσης τῶν δύο προηγούμενων ρυθμῶν.
Ἔτσι γιὰ παράδειγμα ἕναν τριγωνικὸ ὀχτάρι ρυθμὸ τὸν σχεδιάζουμε μὲ πρόσθεση ἑνὸς τριγωνικοῦ πεντάρι ρυθμοῦ καὶ ἑνὸς τριγωνικοῦ τριάρι. Ἡ διαφορετικὴ σειρὰ ποὺ θὰ έμφανίζονται οἱ ἐπιμέρους ρυθμοὶ στὸ μέτρο, ἀλλὰ καὶ ἡ διαφορετικὴ μορφή αυτῶν, κάθε φορὰ θὰ μᾶς δίδη καὶ διαφορετικὴ παραλλαγὴ τοῦ ρυθμοῦ. Ἀντίστοιχα ὁ τριγωνικὸς πεντάρι ρυθμὸς θὰ προκύπτη ἀπὸ τὴν σύνθεση ἑνὸς τριγωνικοῦ τριάρι ρυθμοῦ μὲ ἕναν τριγωνικὸ δυάρι.
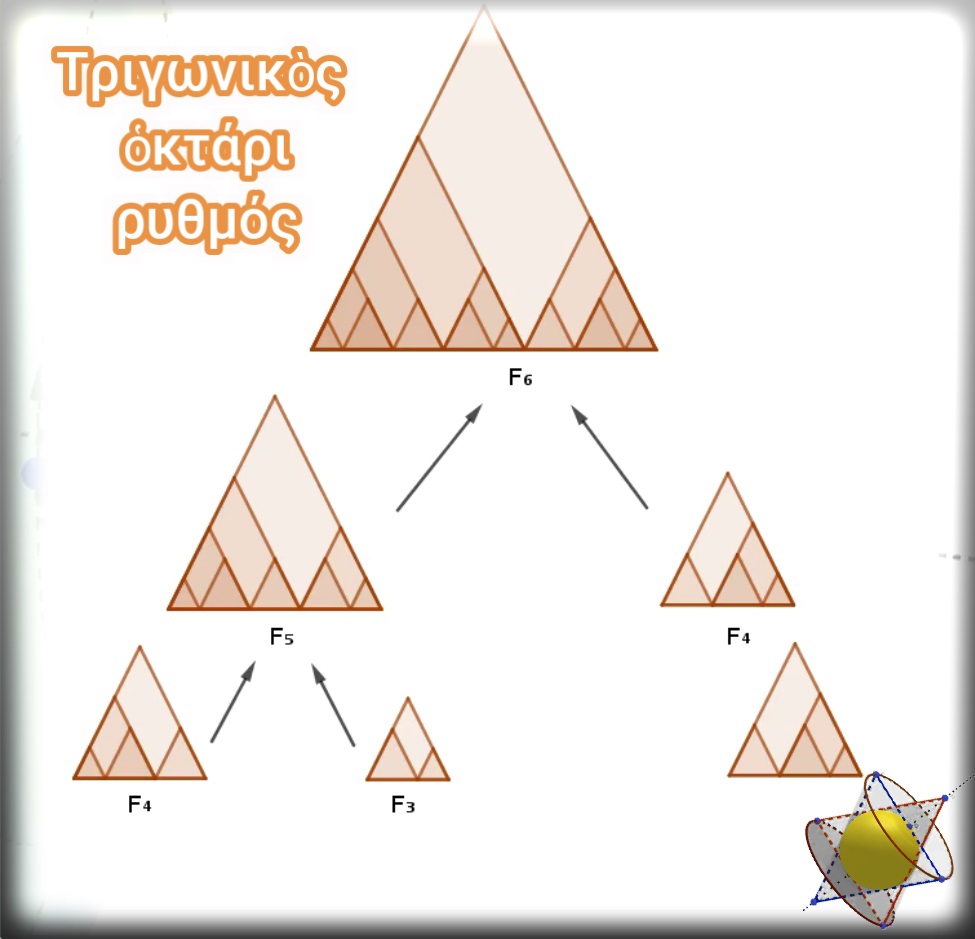
Ἔτσι ὅμως δημιουργήσαμε ἕναν πολὺ συγκεκριμένο τριγωνικὸ ὀχτάρι ρυθμὸ ἐπὶ χάρτου. Θὰ τὸν ζωντανέψουμε. Μὲ τὴ βοήθεια τῆς σύγχρονης μουσικῆς τεχνολογίας, ἐπενδύσαμε τὸ μέτρο μὲ ψηφιακοὺς ἤχους drums, ἄψογα παιγμένους μὲ τοὺς κανόνες καὶ τὶς ὑποδείξεις τοῦ συγκεκριμένου μέτρου.
Τὸ ἀποτέλεσμα τὸ ἀκοῦμε.
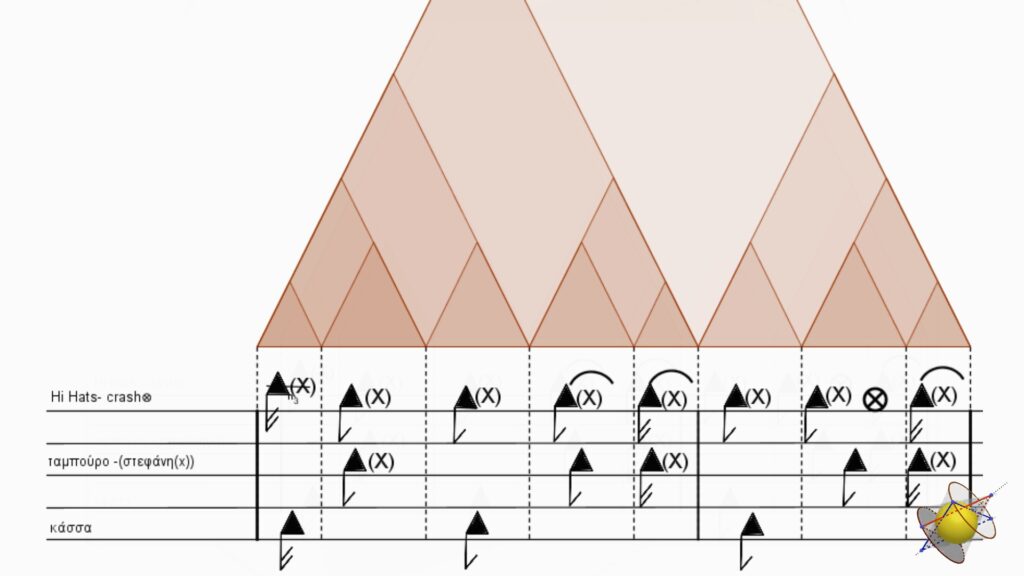
Ἡ ἐπιλογὴ τοῦ συγκεκριμένου τριγωνικοῦ ὀχτάρι ρυθμοῦ δὲν ἦταν τυχαία. Ἔγινε μὲ σκοπὸ νὰ τὸν παντρέψουμε μὲ τὸ μελωδικὸ μέτρο ἀπὸ τὸν πυρρίχιο ποὺ καὶ πιὸ πρὶν ἀκούσαμε, ἔτσι ὥστε νὰ ταυτοποιήσουμε, ἐάν γίνεται, τὸν ρυθμὸ τοῦ συγκεκριμένου μέτρου, ἀλλὰ καὶ γιὰ νὰ ἐνισχύσουμε ἔτσι τὴν πεποίθηση μας γιὰ τὴν ὀρθότητα τοῦ ἐγχειρήματος.
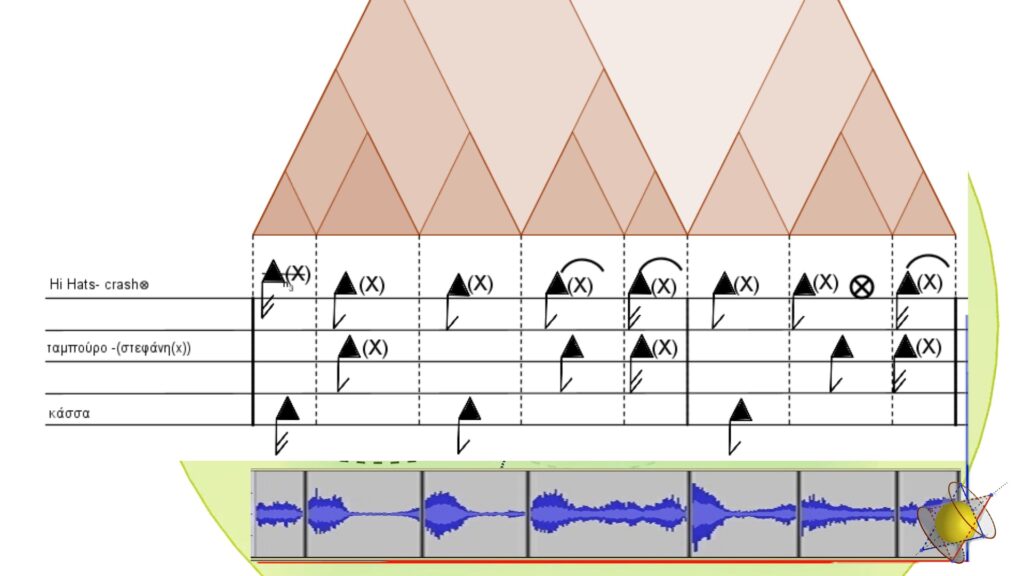
Τὸ ἀποτέλεσμα ἐντυπωσιάζει ὄχι μόνο γιατί ταυτοποιήθηκε ὁ ρυθμός τοῦ δεδομένου μέτρου ἀπὸ τὸν πυρρίχιο, ἐντυπωσιάζει γιατί άποδείχτηκε πὼς αὐτὸ ποὺ ἐδῶ μελετούμε δὲν εἶναι ἕνας ἁπλὸς γεωμετρικὸς μηχανισμὸς ποὺ παράγει μουσικοὺς ρυθμούς, ἐνδεχομένως στὸ χῶρο τοῦ φανταστικοῦ. Ἀποδείχτηκε πὼς οἱ κατὰ φ μουσικοὶ ρυθμοὶ προϋπήρχαν καὶ αὐτὸ ποὺ ἐμεῖς κάναμε ἦταν νὰ τοὺς ἀνακαλύψουμε. Αὐτοὶ έμφανίστηκαν στὴν ἀρχαία Ἑλλάδα, συμβάλλοντας πολυδιάστατα στὴν γέννηση τοῦ πολιτισμοῦ μας, στὴν γέννηση τοῦ παγκόσμιου πολιτισμοῦ. Στὴ συνέχεια ὅμως λησμονήθηκαν και τώρα εἴμαστε ἐδῶ γιὰ νὰ τοὺς θυμηθούμε ξανά, νὰ τοὺς ἀποδεχτούμε, ἀλλὰ καὶ νὰ τοὺς ἐφαρμόσουμε, παρακάμπτοντας τὴν βασικὴ αἰτία τοῦ ἀφανισμοῦ τους, παρακάμπτοντας δηλαδὴ τὴν χρήση τοῦ μετρονόμου, ἡ ὁποία στὴν πραγματικότητα ἐπιβλήθηκε στὴ μουσική, περιορίζοντας δυστυχῶς δραματικὰ τὶς δυνατότητές της.
