Ἡ μελοποιημένη ἀρχαία ἑλληνικὴ ποίηση
Σειρὰ Χ καὶ Μέγα Ἐλλειπτικοὶ Ρυθμοί.
Θὰ ἐπαναλάβουμε τὴν ἴδια τεχνικὴ γιὰ μία ἀκόμα φορά, μόνο ποὺ τώρα θὰ ξεκινήσουμε ἀπὸ τὴν σειρὰ Lucas, ὅπου ἀντὶ στὴν τιμὴ τοῦ κάθε ὅρου της νὰ προσθέσουμε τὴν τιμὴ τοῦ προηγούμενου ὄρου της, γιὰ νὰ βρεθοῦμε στὸν ἑπόμενο, θὰ προσθέτουμε τὴν τιμὴ τοῦ πρὸ προηγούμενου ὄρου. Ἔτσι ὅμως, κάθε φορὰ θὰ παίρνουμε τὴν τιμὴ τοῦ ἀντίστοιχου ὄρου μίας νέας σειράς, μίας νέας σειρᾶς ἡ ὁποία, ἐπειδὴ δὲν ἔχει ἀκόμα ὄνομα, θὰ τὴν ὀνομάσουμε προσωρινὰ σειρὰ Χ. Καὶ ἡ σειρὰ Χ παρόμοιες ἰδιότητες μὲ αὐτὲς τῶν σειρῶν Fibonacci καὶ Lycas ἔχει. Καὶ στὴ σειρὰ Χ, ὁ κάθε ἑπόμενος ὄρος ἔχει τιμὴ ἴση μὲ τὸ ἄθροισμα τῶν τιμῶν τῶν δύο προηγουμένων ὄρων.
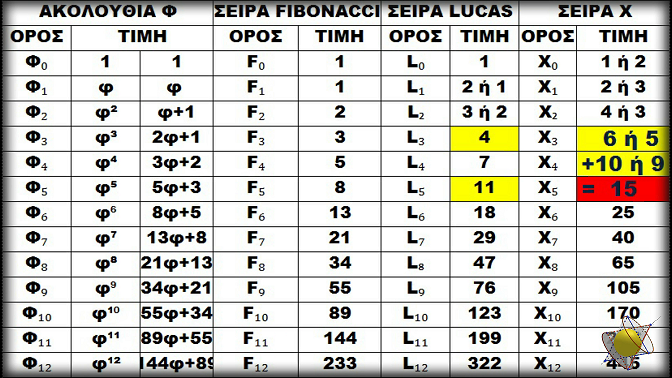
Ἡ σειρὰ Χ, τὴν ὁποία πρώτη φορὰ παρουσίασα στὴν 7ἡ διεθνὴ μαθηματικὴ ἑβδομάδα τὸν Μάρτιο τοῦ 2015 στὴν Θεσσαλονίκη, εἶναι ἰδιαίτερα σημαντικὴ ὄχι μόνο λόγῳ τῆς συμβολῆς της στὴν δημιουργία τῶν μουσικῶν ρυθμῶν, εἶναι ἰδιαίτερα σημαντικὴ γιατὶ μὲ τὴν ἐμφάνισή της ὁλοκληρώθηκε ὁ ἀριθμὸς τῶν θυγατρικῶν σειρῶν τῆς ἀκολουθίας Φ, δηλαδὴ τῶν σειρῶν Fibonacci, Lucas καὶ X καὶ ἔτσι μπόρεσε νὰ φανῆ συνολικὰ ἡ μεταξὺ τους σχέση.
Μέσα ἀπ’αυτήν τὴν συνολικὴ εἰκόνα φαίνεται πὼς ἕνα περιοδικὸ φαινόμενο ἐκτελεῖ ἕναν πλήρη κύκλο τοῦ φαινομένου μετὰ ἀπὸ δώδεκα ἐξελικτικὰ βήματα, ὅπως ἀκριβῶς συμβαίνει καὶ μὲ τὴ μουσική. Ἐκτελεῖ ἕναν πλήρη κύκλο ὅμως ὄχι μόνο μεταφορικά, ἀλλὰ καὶ κυριολεκτικά, καθὼς γιὰ ἀκόμα φορὰ ἐμπλέκεται ὁ ἀριθμὸς Φ.
Αὐτὴ ἡ ταυτόχρονη ἐμφάνιση σχέσεων, λόγων, σειρῶν, παγκόσμιων σταθερῶν, ἀλλὰ καὶ συμβόλων καὶ μηχανισμῶν, μὲ ὁδήγησαν στὴν σύλληψη ἑνὸς μοντέλου γιὰ τὸ Σύμπαν ἰδιαίτερα πιστικοῦ, τὸ ὁποῖο μπορεῖ στὴν ἀρχὴ νὰ στηρίχτηκε σὲ κανόνες μουσικῆς καὶ ἁρμονίας, ἀλλὰ ὑποστηρίζει καὶ ὑποστηρίζεται τόσο ἀπὸ τεκμηριωμένες ἐπιστημονικὲς ἀνακαλύψεις, ὅσο κι’ ἀπὸ φιλοσοφικὲς ἀλλὰ καὶ θεολογικὲς ἀπόψεις γιὰ τὸν κόσμο. Ἐδῶ ὅμως θὰ δοῦμε πὼς ἡ σειρὰ Χ συμβάλει στὴ μουσικὴ καὶ στὴ δημιουργία μουσικῶν ρυθμῶν.
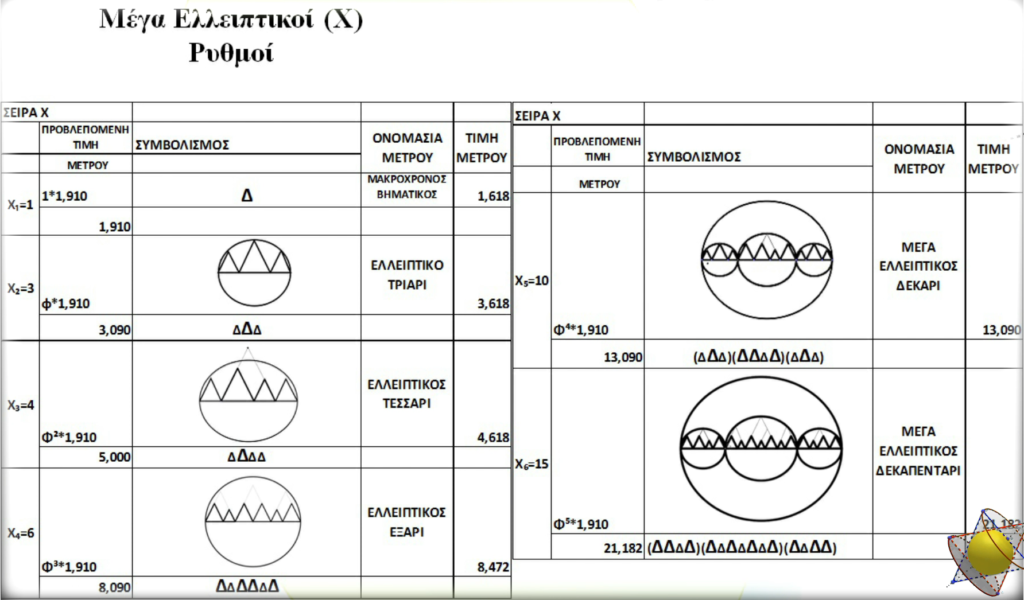
Παίρνουμε τρεῖς συνεχόμενους ὄρους τῆς σειρᾶς Lucas μαζὶ μὲ τοὺς ἀντίστοιχους ἐλλειπτικοὺς ρυθμούς, τὸν ἐλλειπτικὸ τριάρι, τὸν ἐλλειπτικὸ τεσσάρι καὶ τὸν ἐλλειπτικὸ ἑφτάρι ρυθμό. Ἐὰν τώρα στὸ ἐλλειπτικὸ ἑφτάρι ρυθμὸ προσθέσουμε τὸν πρὸ προηγούμενο του, δηλαδὴ τὸν ἐλλειπτικὸ τριάρι ρυθμό, τότε θὰ πάρουμε ἕναν νέο ρυθμό, ὁ ὁποῖος στὴν ἀρτιώτερη, τουλάχιστον σχεδιαστικά μορφή, θὰ μποροῦσε νὰ ἀποδοθῆ ἀπὸ μία μεγάλη ἔλλειψη μέσα στὴν ὁποία θὰ ἐμφανίζονται τρεῖς μικρότερες ἐλλείψεις.
Φυσικά, ἡ κάθε ἐπιμέρους ἔλλειψη, ρυθμικὰ θὰ μποροῦσε νὰ ἀποδοθῆ μὲ τρεῖς συγκεκριμένους τριγωνικοὺς ρυθμούς. Γιὰ αὐτό, τοὺς ρυθμοὺς τῆς κατηγορίας θὰ τοὺς ὀνομάσουμε Μέγα Ἐλλειπτικοὺς Ρυθμούς. Θὰ τοὺς ὀνομάσουμε ὅμως καὶ Χ ρυθμούς, γιὰ νὰ τονίσουμε τὴν σημασία τῆς σειρᾶς Χ στὴν δημιουργία τους. Στὸν πίνακα ποὺ ἀκολουθεῖ βλέπουμε συγκεντρωτικὰ τὶς πρῶτες ὁμάδες τῶν μέγα ἐλλειπτικῶν ρυθμῶν.
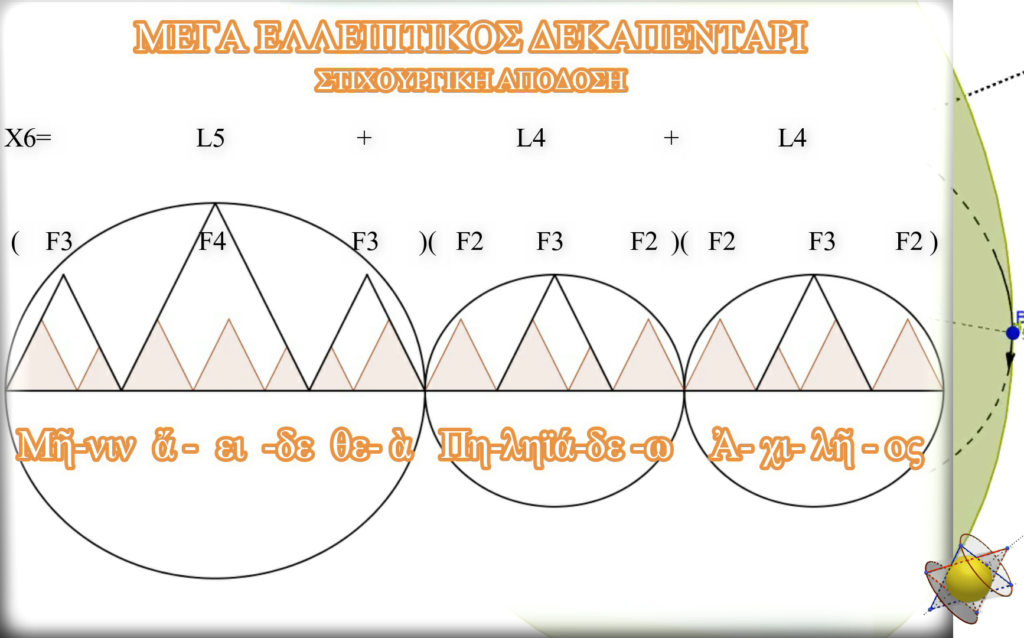
Θὰ πρέπει καὶ πάλι νὰ ἐπισημανθῆ πὼς οἱ ρυθμοὶ εἶναι ὅλοι σύνθετοι, μόνο ποὺ ἐδῶ οἱ δυνατότητες ἐπιλογῆς τῶν ἐπιμέρους ρυθμῶν ποὺ θὰ ἀπαρτίζουν τὸ μέτρο, καθὼς ἐπίσης καὶ οἱ δυνατότητες ἐπιλογῆς τῆς μορφῆς αὐτῶν, καθὼς καὶ τῆς σειρᾶς ποὺ αὐτοὶ θὰ ἐμφανίζονται μέσα στὸ μέτρο, θὰ εἶναι πολὺ περισσότερες. Ἔτσι, ἀντίστοιχα πολὺ περισσότερες θὰ εἶναι καὶ οἱ δυνατὲς παραλλαγὲς τῶν ρυθμῶν. Εἶναι κάτι ποὺ θὰ φανῆ ἰδιαίτερα χρήσιμο, τόσο σὲ ρυθμικὸ καὶ μελωδικὸ ἐπίπεδο, ὅσο καὶ σὲ στιχουργικὸ ἐπίπεδο, ὅπως θὰ δοῦμε στὴν συνέχεια. Ἐδῶ θὰ ἐπικεντρωθοῦμε στὸν Χ₆ ρυθμὸ, στὸν ρυθμὸ μέγα ἐλλειπτικὸ δεκαπεντάρι. Ἕναν τέτοιο ρυθμὸ θὰ προσπαθήσουμε νὰ δημιουργήσουμε.
Ἕνας Χ₆ ρυθμὸς μπορεῖ νὰ προκύψη ἀπὸ τὴν σύνδεση τῶν δύο προηγούμενων ρυθμῶν του, δηλαδὴ ἀπὸ τὴν σύνδεση ἑνὸς Χ₅ ρυθμοῦ μὲ ἕναν Χ₄ ρυθμό. Ἐδῶ, θὰ προσπαθήσουμε νὰ τὸν δημιουργήσουμε ἀπὸ τὴν σύνθεση τοῦ ἀντίστοιχου ἐλλειπτικοῦ ρυθμοῦ μὲ τὸν πρὸ προηγούμενο του, δηλαδὴ ἀπὸ τὴν σύνθεση ἑνὸς L₆ ρυθμοῦ μὲ ἕναν L₄.
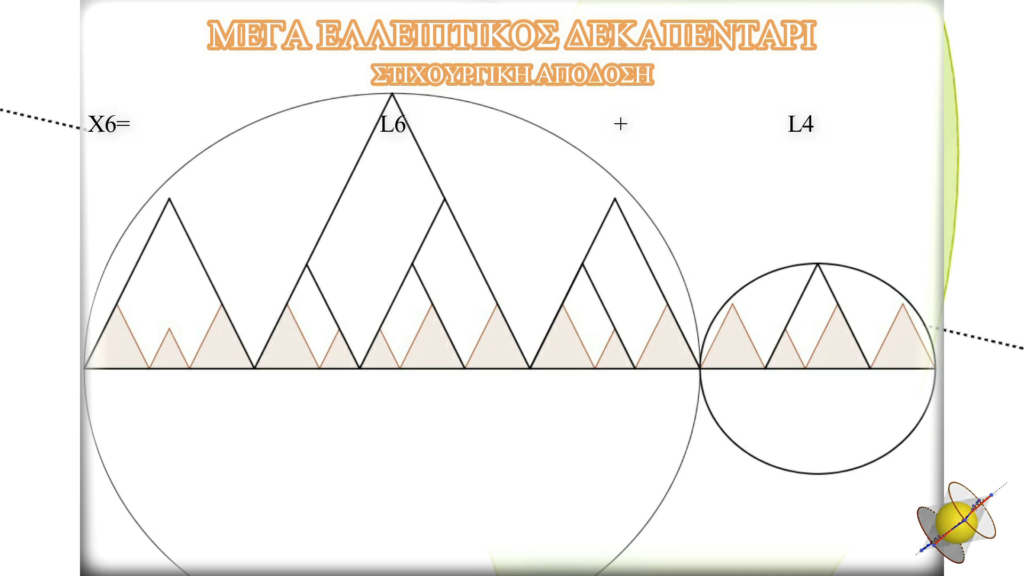
Ἀντίστοιχα καὶ ὁ L₆ ρυθμὸς μπορεῖ νὰ προκύψη ἀπὸ τὴ σύνθεση ἑνὸς L₅ ρυθμοῦ μὲ ἕναν L₄. Φυσικά, ὁ κάθε ἐπιμέρους L ρυθμὸς θὰ ἀποτελεῖται ἀπὸ τρεῖς συγκεκριμένους τριγωνικοὺς ρυθμούς. Ἔτσι, μποροῦμε νὰ φανταστοῦμε τὸν τεράστιο ἀριθμὸ τῶν δυνατῶν, ἀλλὰ καὶ ἐπιτρεπτῶν μορφῶν ἑνὸς Χ₆ ρυθμοῦ.
Μιὰ τέτοια μορφὴ ρυθμοῦ εἶναι καὶ αὐτὴ ἡ ὁποία βλέπουμε.
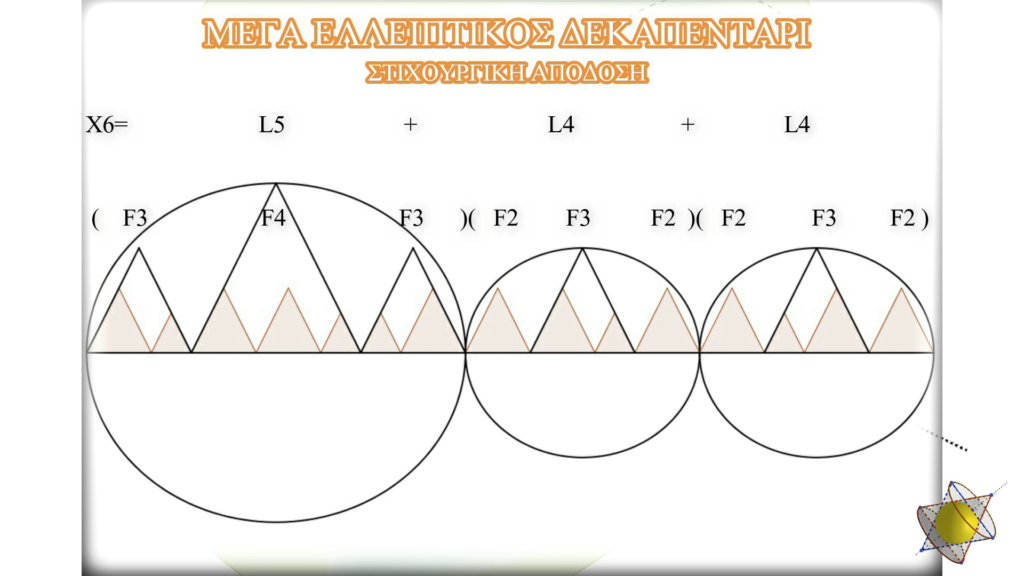
Τὸ ἐρώτημα μας εἶναι ἁπλό. Μπορεῖ ἕνας τέτοιος ρυθμὸς νὰ ὑποστηρίξη ρυθμικὰ καὶ στίχο;
Ἄς ἐπιτρέψουμε στὸν πρῶτο στίχο τῆς Ἰλιάδος νὰ ἀναδυθῆ.
Καταρχὴν βλέπουμε ὁ στίχος νὰ καλύπτη ἐπακριβῶς τὸ μέτρο μὲ τὶς συλλαβὲς του.
Βλέπουμε τὶς μακρόχρονες συλλαβὲς νὰ ταυτίζονται μὲ μακρόχρονες ἀξίες τοῦ ρυθμοῦ.
Βλέπουμε τὶς βραχύχρονες συλλαβὲς νὰ περνοῦν θέση κάτω ἀπὸ βραχύχρονες ἀξίες, ἀλλὰ καὶ ἀπὸ μακρόχρονες, ὅταν αὐτὲς βρίσκονται στὴν ἀρχὴ ἢ στὸ τέλος μίας λέξης, ἐπιτρέποντας μὲ αὐτὸν τὸν τρόπο τὴν ἐμφάνιση μικρῶν παύσεων, ἀπαραίτητων γιὰ τὶς ἀναγκαῖες ἀνάσες.
Οἱ δίχρονες συλλαβές, μέσα καὶ ἀπὸ γνωστοὺς γραμματικοὺς κανόνες, ἀποκτοῦν ἄλλοτε μακρόχρονη καὶ ἄλλοτε βραχύχρονη συμπεριφορά, ἐπιβεβαιώνοντας καὶ ὑποστηρίζοντας κάθε φορὰ τὸν ρυθμό.
Γενικώτερα βλέπουμε τὸ λόγο ὕπαρξης μακρόχρονων καὶ βραχύχρονων συλλαβῶν.
Ὑπάρχει ὅμως καὶ ἕνας νοηματικὸς διαχωρισμὸς τοῦ στίχου σὲ τμήματα, τὰ ὁποία ἀντιστοιχοῦν στοὺς ἐπιμέρους ρυθμοὺς τοῦ μέτρου. Ἔτσι, ἔχουμε τὴν κύρια πρόταση «μῆνιν ἄειδε θεά», ἡ ὁποία μὲ τὴν παρουσία της καλύπτει τὸν πρῶτο L₅ ρυθμό. Μάλιστα, οἱ τρεῖς λέξεις ποὺ ἀποτελοῦν τὴν πρόταση, ἐμφανίζονται μὲ τὸν κατάλληλο ἀριθμὸ συλλαβῶν καὶ μὲ τὴν κατάλληλη σειρά, ἔτσι ὥστε νὰ μπορέσουν νὰ πλαισιώσουν σωστὰ τοὺς τρεῖς ἐπιμέρους τριγωνικοὺς ρυθμοὺς τοῦ L₅ ρυθμοῦ μας. Ὁ προσδιορισμὸς «Πηληιάδεω» καλύπτει τὸν πρῶτο ἀπὸ τοὺς δύο L₄ ρυθμοὺς καὶ ἡ λέξη «Ἀχιλῆος» τὸν δεύτερο.
Τέλος βλέπουμε ἕναν ἀνορθόγραφο «Ἀχιλῆος» ὁ ὁποῖος ὑπάρχει γιὰ νὰ ἐπιβεβαιώση τὰ λεγόμενα. Ἡ λέξη γραμμένη μὲ ἕνα λάμδα ἐπιτρέπει στὴν προπαραλήγουσα –χι- νὰ εἶναι βραχύχρονη. Ἐὰν ἡ λέξη ἦταν γράμμενη μὲ δὐο λάμδα, ὅπως θὰ ἦταν γραμματικὰ τὸ σωστό, ἡ προπαραλήγουσα θὰ ἦταν μακρόχρονη, ἔτσι ὅμως θὰ ὑπῆρχε πρόβλημα.
Αὐτὴ λοιπὸν εἶναι καὶ ἡ μορφὴ τοῦ Χ₆ ρυθμοῦ μᾶς ἡ ὁποία μπορεῖ νὰ ὑποστηρίξει ρυθμικὰ τὸν πρῶτο στίχο τῆς Ἰλιάδος.Σὲ αὐτὴν ὅμως τὴν μορφὴ δὲν ἔχουμε τὴν ἐμφάνιση μίας μεγάλης ἔλλειψης, τὸ ὁποῖο εἶναι καὶ τὸ ἐπιθυμητό. Γιὰ νὰ μπορέση αὐτὴ νὰ φανῆ, θὰ πρέπει νὰ δοῦμε τὸν ρυθμὸ διαφορετικά.
Τὰ τέσσερα σημεῖα, τὰ ὁποῖα χαρακτηρίζουν τὴν μεγάλη ἔλλειψη, δηλαδὴ τὰ δύο ἄκρα της καὶ οἱ δύο ἑστίες της, εἶναι τὰ τέσσερα σημεῖα τὰ ὁποῖα θὰ τονίζουν τὸν ρυθμὸ καὶ τὰ ὁποῖα θὰ ἐπαναλαμβάνονται σὲ κάθε νέο μέτρο, σὲ κάθε ἑπόμενο στίχο.
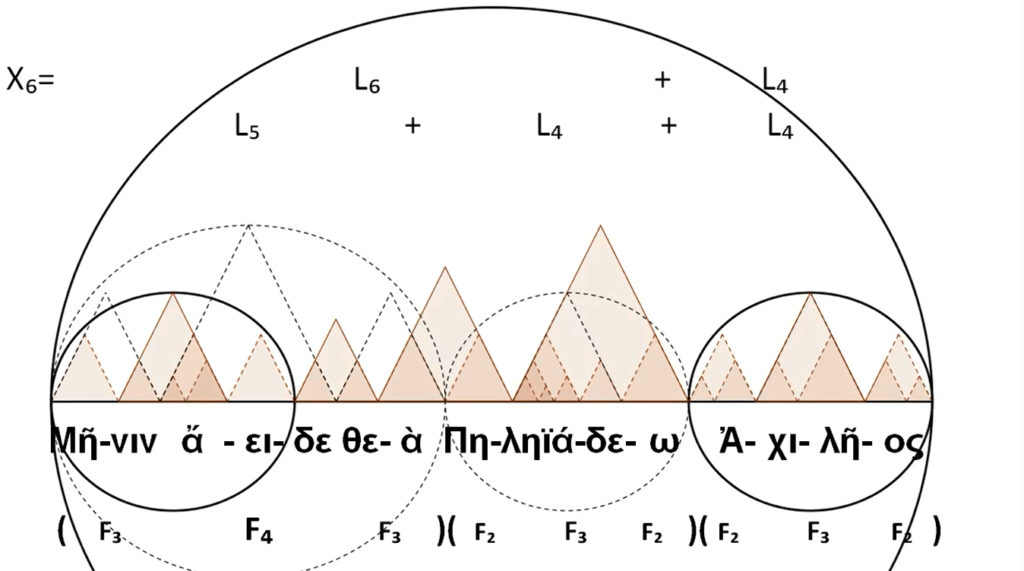
Αὐτὰ εἶναι λοιπὸν συνολικὰ τὰ συμπεράσματα τὰ ὁποῖα προέκυψαν γιὰ τὸν ρυθμὸ τοῦ πρώτου στίχου τῆς Ἰλιάδος.
Σὲ ἀνάλογα ὅμως συμπεράσματα κατέληξα καὶ γιὰ τοὺς ἑπόμενους ἕξι στίχους αὐτῆς, τὰ ὁποῖα φωτογραφικὰ θὰ δοῦμε. Ταυτόχρονα, μὲ τὸ ρυθμὸ τὸν ὁποῖο θὰ ἀκοῦτε, θὰ ἤθελα νὰ προσέξετε καὶ τή μελωδία. Θὰ ἤθελα νὰ παρατηρήσετε τὴν τονικότητα τῆς κάθε νότας καὶ νὰ δῆτε ἐὰν καὶ κατὰ πόσο αὐτὴ θὰ μπορεῖ νὰ ταυτίζεται μὲ τὴν φωνὴ πού κάθε φορὰ θὰ παράγεται ἀπὸ τὸ φωνῆεν τῆς ἀντίστοιχης συλλαβῆς. Τὸ ἀποτέλεσμα τῆς παρατήρησης θεωρῶ πὼς τουλάχιστον θὰ προβληματίση.