Ὁ τετραγωνισμὸς τοῦ κύκλου στὸ Πὶ καὶ Φί
Σειρὰ Lucas
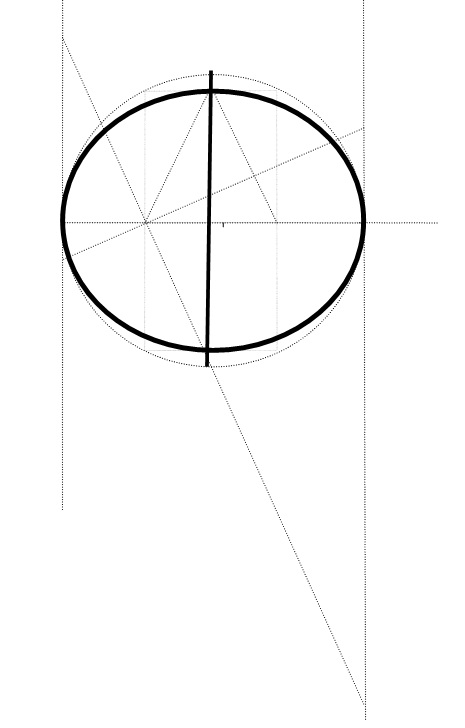
Ἀπό τὸ βιβλίο…

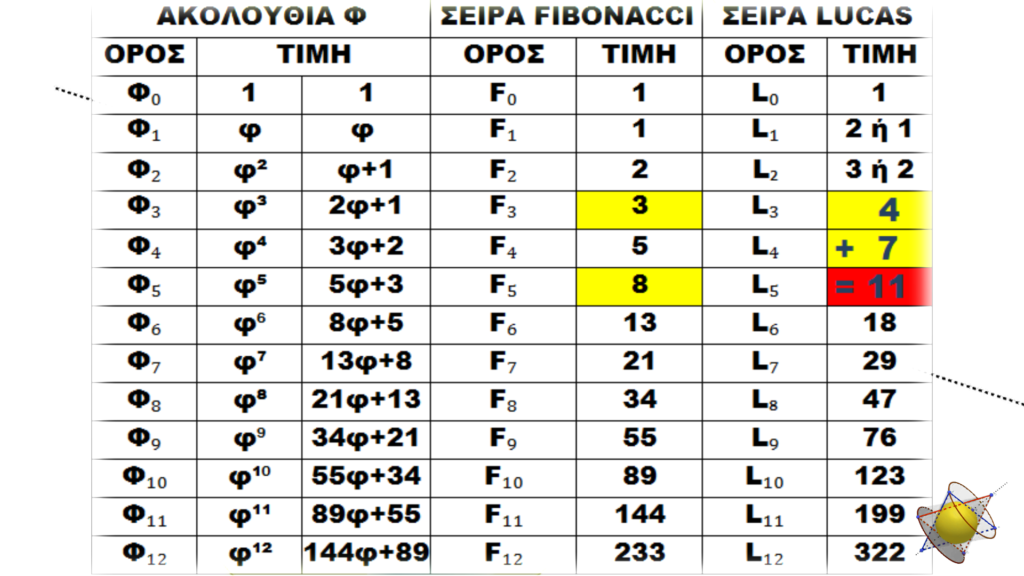
Ὅπως εἴδαμε, στὴν σειρὰ Fibonacci, γιὰ νὰ πᾶμε στὸν ἑπόμενο ὅρο, δηλαδὴ στὸ ἑπόμενο βῆμα, προσθέτουμε στὸν ὑπάρχοντα ὅρο τὸν προηγούμενο. Ἔτσι, γιὰ νὰ πᾶμε στὸν τρίτο ὅρο προσθέτουμε στὸν δεύτερο ὅρο, στὸν ὁποῖο βρισκόμαστε, τὸν πρῶτο. Γιὰ νὰ πᾶμε στὸν τέταρτο ὅρο, προσθέτουμε στὸν τρίτο ὅρο τὸν δεύτερο καὶ συνεχίζουμε…
Ἐὰν ὅμως στὸν κάθε ὅρο τῆς σειρὰς Fibonacci προσθέσουμε τὸν προ-προηγούμενο ὅρο της, τότε σχηματίζεται μία ἄλλη σειρὰ ἀριθμῶν, γνωστὴ σὰν σειρὰ Lucas. Ἂς δοῦμε καταρχὴν τὸν παρακάτω πίνακα.
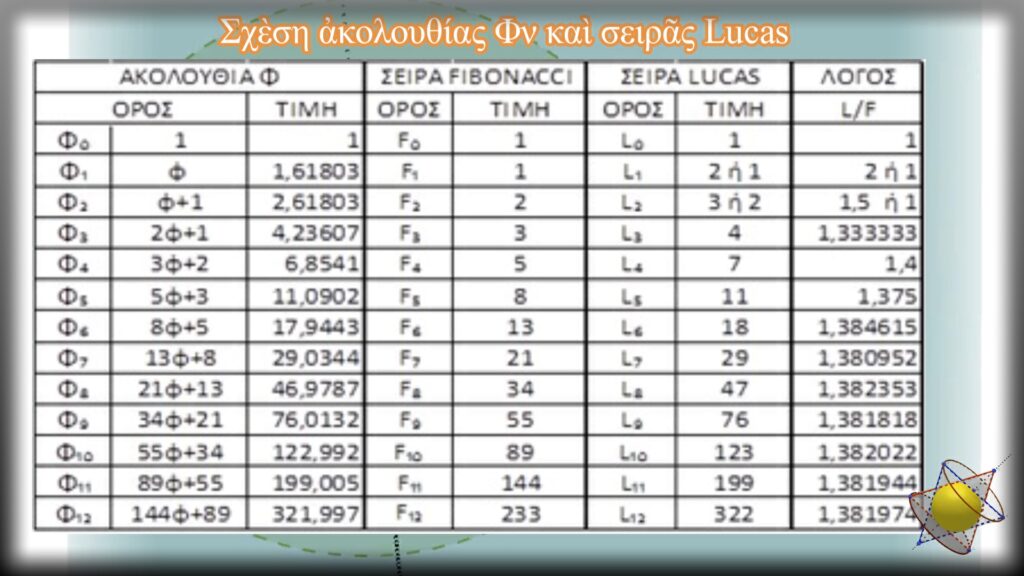
Τὰ ἄμεσα ἐξαγόμενα συμπεράσματα ποὺ προκύπτουν εἶναι τὰ ἀκόλουθα:
– Ἡ σειρὰ Lucas προέρχεται ἀπὸ τὴ σειρὰ Fibonacci.
– Ἡ σειρὰ Lucas εἶναι ΑΠΛΑ ἡ ἀκολουθία Φν στρογγυλοποιημένη στὸν πιὸ κοντινὸ ἀκέραιο ἀριθμό. Ὁ 2ος ὅρος μπορεῖ νὰ πάρει τὴν τιμὴ 2 (ἐπικρατέστερη), σὰν ὁ πιὸ κοντινὸς ἀκέραιος στὴν τιμὴ τοῦ ἀριθμοῦ φ=1,618034… ἀλλὰ καὶ τὴν τιμὴ 1. Ἀντίστοιχα τὸ ἴδιο συμβαίνει καὶ μὲ τὸν 3ο ὅρο ποὺ μπορεῖ νὰ πάρει τὶς τιμὲς 3 (ἐπικρατέστερη) ἢ 2.
– Ὅπως στὴν σειρὰ Fibonacci ἔτσι καὶ στὴν σειρὰ Lucas μποροῦμε ἀπὸ ὁποιοδήποτε ὅρο της νὰ προχωρήσουμε στὸν ἑπόμενο, προσθέτοντας σὲ αὐτὸν τὸν προηγούμενο. Ἡ ἐπικρατοῦσα τιμὴ 4 στὸν τέταρτο ὄρο προκύπτει σὰν τὸ ἀποτέλεσμα ἄθροισης τοῦ 4ου καὶ τοῦ 2ου ὄρου τῆς σειρὰς Fibonacci, ἀλλὰ καὶ σὰν τὸ πιθανώτερο ἀποτέλεσμα ἄθροισης τοῦ 3ου καὶ τοῦ 2ου ὅρου τῆς σειρὰς Lucas.
– Κατ’ ἀναλογία τῆς ἀκολουθίας Φν καὶ τῆς σειρὰς Fibonacci, ὁ κάθε ὅρος τῆς σειρᾶς Lucas μπορεῖ νὰ δοθεῖ καὶ σὰν ἄθροισμα τῶν προηγούμενων ἀπὸ τὴ σχέση:
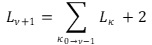
Σὰν ἄθροισμα τῶν ὅρων L1 kai L2 λογαριάζεται ὁ ἀριθμὸς 4 , ἀποτέλεσμα τῆς πράξης 2+2 ἢ 3+1 τῶν ἀντίστοιχων ὅρων.
Ὅπως καὶ στὴν προηγούμενη περίπτωση, ὅπου, ὅσο προχωροῦμε, ὁ λόγος τῶν τιμῶν τῶν ἀντίστοιχων ὅρων τῆς ἀκολουθίας Φν καὶ τῆς σειρᾶς Fibonacci τείνει στὸν ἀριθμὸ 1,382… ἔτσι καὶ ἐδῶ, ὁ λόγος τῶν τιμῶν τῶν ἀντίστοιχων ὅρων Lucas – Fibonacci τείνει στὸν ἴδιο ἀριθμὸ
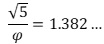
Τὴ σημασία τῆς σειρᾶς Lucas τὴν ἔχουμε ἤδη δεῖ στὴ δημιουργία τῶν ἐλλειπτικῶν μουσικῶν ρυθμῶν (ἐδῶ).

