Ὁ τετραγωνισμὸς τοῦ κύκλου στὸ Πὶ καὶ Φί
Εὔρεση τοῦ άριθμοῦ π - Ὁ τετραγωνισμὸς τοῦ κύκλου (προσεγγιστικά;)
Άπὸ τὸ βιβλίο…

Ἂς προχωρήσουμε στὸ ἑπόμενο στάδιο ἀνάπτυξης τοῦ γεωμετρικοῦ μηχανισμοῦ.
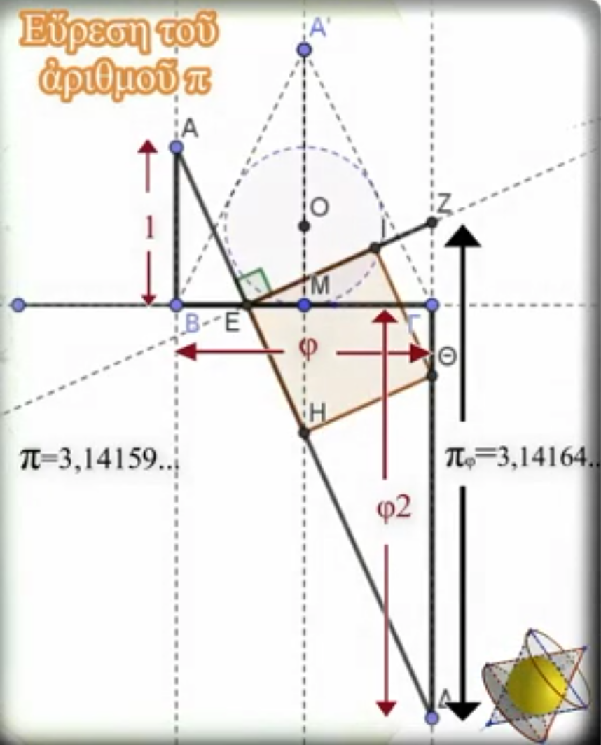
Κατασκευάζουμε τὸ χρυσὸ τρίγωνο Α΄ΒΓ, μὲ βάση ΒΓ=φ καὶ τὸν ἐγγεγραμμένο του μοναδιαίο κύκλο.
Ἀπὸ τὰ σημεῖα Β καὶ Γ φέρνουμε εὐθεῖες κάθετες στὸ ΒΓ εὐθύγραμμο τμῆμα. Στὴν πρώτη κάθετη εὐθεία κατασκευάζουμε τὸ ΑΒ εὐθύγραμμο τμῆμα τὸ ὁποῖο θὰ εἶναι ἴσο μὲ τὴ μονάδα, ἴσο μὲ τὴ διάμετρο τοῦ ἐγγεγραμμένου κύκλου τοῦ χρυσοῦ τριγώνου. Στὴ συνέχεια, στὴ δεύτερη κάθετη εὐθεία παίρνουμε τὸ εὐθύγραμμο τμῆμα ΓΔ ἴσο μὲ φ² , ἴσο μὲ ΑΒ+ΒΓ, καθὼς ἰσχύει 1+φ=φ².
Ἔτσι, ἡ συγκεκριμένη κατασκευὴ μᾶς ἔδωσε τρία συνεχόμενα εὐθύγραμμα τμήματα μὲ ἀναλογίες Φ καὶ κάθετα μεταξὺ τους, θὰ μπορούσαμε νὰ ποῦμε σὲ μιὰ μαιανδρική διάταξη. Ἀκολούθως, φέρνουμε τὸ ΑΔ εὐθύγραμμο τμῆμα, τὸ ὁποῖο τέμνει τὸ ΒΓ στὸ σημεῖο Ε. Κατόπιν, κατασκευάζουμε εὐθεία κάθετη στὸ ΑΔ εὐθύγραμμο τμῆμα ποὺ περνάει ἀπὸ τὸ σημεῖο Ε καὶ ἡ ὁποία τέμνει τὴν ε₂ εὐθεία στὸ σημεῖο Ζ.
Τὸ εὐθύγραμμο τμῆμα ΖΔ ποὺ προκύπτει ἀποδεικνύεται (ἐδῶ) ὅτι εἶναι ἴσο μὲ 3,14164…
ΖΔ=6/5•φ²=3,14164…
Τὴν τιμὴ αὐτὴ θὰ τὴν ὀνομάσουμε πφ καὶ γιὰ νὰ ξεχωρίζει ἀπὸ τὴν ἰσχύουσα τιμὴ τοῦ ἀριθμοῦ π 3,14159…, ἀλλὰ καὶ γιὰ νὰ τονίσουμε τὴν προέλευση της. Ἡ ἀπόκλιση εἶναι τῆς τάξης τοῦ 10-4
Εἶναι μικρὴ ἀλλὰ ὄχι ἀμελητέα, κάτι τὸ ὁποῖο δὲν μᾶς ἐπιτρέπει νὰ ἰσχυριστοῦμε ὅτι κατασκευάσαμε γεωμετρικὰ τὸν ἀριθμὸ π. Ἔχει τεράστιο ὅμως ἐνδιαφέρον ἡ τιμὴ τῆς ἀπόκλισης, τιμὴ ἡ ὁποία θὰ ἐμφανιστεῖ καὶ πάλι μὲ μιὰ τελείως διαφορετικὴ διαδρομή. Ἡ μαθηματικὴ της ἐξήγηση μέσα ἀπὸ ἕνα νέο μουσικό, κοσμογονικὸ μοντέλο εἶναι τοὐλάχιστον συναρπαστική.
Γιὰ τὴν ὥρα ὅμως , ἂς κρατήσουμε τὸν ἁπλὸ καὶ ἁρμονικὸ τρόπο ποὺ προέκυψε ὁ ἀριθμὸς πφ.
Ὁ μηχανισμὸς ὅμως συνεχίζει νὰ μᾶς ἐκπλήσσει.
Ἡ μεσοκάθετος τοῦ ΒΓ εὐθυγράμμου τμήματος τέμνει τὸ ΑΔ εὐθύγραμμο τμῆμα στὸ σημεῖο Η (μέσον τοῡ ΑΔ). Ἀπὸ τὸ σημεῖο Η φέρνουμε εὐθεία κάθετη στὸ ΑΔ, ἡ ὁποία τέμνει τὸ ΓΔ εὐθύγραμμο τμῆμα στὸ σημεῖο Θ. Νέα κάθετος στὸ ΗΘ εὐθύγραμμο τμῆμα , ἀπὸ τὸ σημεῖο Θ τέμνει τὸ ΕΖ εὐθύγραμμο τμῆμα στὸ σημεῖο Ι.
Ἀποδεικνύεται (ἐδῶ) ὅτι τὸ ΕΗΘΙ τετράπλευρο εἶναι τετράγωνο μὲ ἐμβαδὸν ἴσο μὲ
6/5·φ2 ·(1/2)2 , δηλαδὴ: Ε(ΕΗΘΙ) =πφ ·(1/2)2.
Ἐὰν λοιπὸν θεωρηθεῖ πὼς πφ=π, τότε τὸ ἐμβαδὸν τοῦ συγκεκριμένου τετραγώνου εἶναι ἴσο μὲ τὸ ἐμβαδὸν τοῦ μοναδιαίου κύκλου, τοῦ ἐγγεγραμμένου δηλαδὴ κύκλου τοῦ χρυσοῦ τριγώνου. Θὰ μπορούσαμε ἔτσι νὰ ἰσχυριστοῦμε πὼς τετραγωνίσαμε τὸν κύκλο.
Ἰσχύει ὅμως;
Ὄχι. Ὅπως γνωρίζουμε, ὁ ἀριθμὸς π εἶναι ὑπερβατικὸς καὶ αὐτὸ καθιστὰ ἀδύνατο τὸν τετραγωνισμὸ τοῦ κύκλου. Ἡ παραπάνω κατασκευή, μόνο προσεγγιστικά μπορεῖ νὰ θεωρηθεῖ πὼς τετραγωνίζει τὸν κύκλο.
Τὰ ἐρωτήματα ὅμως ποὺ δημιουργοῦνται εἶναι βασανιστικά.
Γιατὶ οἱ κατὰ τὰ ἄλλα σοφοὶ τῆς ἀρχαιότητας νὰ φανοῦν τόσο ἀνόητοι καὶ νὰ θέσουν ἄλυτα προβλήματα;
Γιατὶ μὲ τόσο ἁπλὸ καὶ ἁρμονικὸ τρόπο νὰ προκύπτη λύση καὶ μάλιστα στὸ πὶ καὶ φί;
Μήπως μὲ αὐτὸν τὸν τρόπο θέλανε νὰ μᾶς ὁδηγήσουν σὲ ἕναν διαφορετικὸ τρόπο σκέψης ποὺ θὰ μᾶς ἔδινε ἀπαντήσεις σὲ πολὺ σημαντικότερα καὶ ἀνώτερα ἐρωτήματα;
Μήπως ἡ χρήση τῆς παγκόσμιας αὐτῆς σταθερὰς τοῦ ἀριθμοῦ «πφ», σὲ συμπαντικὲς ἐφαρμογές, ὅπου ξεπερνιέται ὁ στενὸς τρισδιάστατος χῶρος μας, προσαρμόζεται ἐνσωματώνοντας καὶ τὴν τέταρτη διάσταση;
Ἔπρεπε ὁπωσδήποτε νὰ τὸ ἐρευνήσω.

