Τετρακτύς
Τετρακτὺς καὶ τὸ "μουσικὸ" τρίγωνο - 1η πυθαγόρεια τριάδα
Ἀπό τὸ βιβλίο…

Ἕως τώρα εἴδαμε τὴ σπουδαιότητα τοῦ ἰδιαίτερου ἰσοσκελοῦς τριγώνου μὲ βάση ἴση μὲ τὸ ὕψος του. Τὸ ἀποκαλέσαμε Χρυσὸ Τρίγωνο γιατὶ περιέχει ὅλες τὶς ἀναλογίες τοῦ ἀριθμοῦ φ, χωρὶς αὐτὲς νὰ γίνονται ἄμεσα ἀντιληπτές. Ἀποδείξαμε πὼς ἐὰν ὁ ἐγγεγραμμένος σὲ αὐτὸν κύκλος εἶναι ὁ μοναδιαῖος, τότε ἡ βάση τοῦ τριγώνου εἶναι ἴση μὲ τὸν ἀριθμὸ φ, ἀλλὰ καὶ ἡ περίμετρος τοῦ κύκλου εἶναι ἴση μὲ τὸν ἀριθμὸ π. Μᾶς δόθηκε ἡ σχέση μεταξὺ τῶν δύο αὐτῶν ἀριθμῶν σὲ συμπαντικὲς τετραδιάστατες ἐφαρμογές. Ὅταν τοποθετήσαμε τέσσερις ἀπολύτως συγκεκριμένες ἀκτίνες εἴδαμε τὸν ἴδιο μηχανισμὸ νὰ ὑποστηρίζει γεωμετρικὰ τὴν στηριζόμενη στὴν πυθαγόρεια ἀναλογία 3:2 μουσικὴ κλίμακα, σὲ λόγους, τιμές, βηματισμὸ καὶ ἀριθμὸ βημάτων ὁλοκλήρωσης τῆς κλίμακας.
Παράλληλα ὅμως ἐμφανίστηκαν καὶ διάφορα γεωμετρικὰ σχήματα ποὺ περιέχουν ζητούμενους μουσικοὺς λόγους. Μερικὰ ἀπὸ αὐτὰ ἀναφέρονται στὴν βιβλιογραφία μου. Ἐδῶ θὰ σταθοῦμε στὸ πιὸ ἐνδιαφέρον γεωμετρικὸ σχῆμα.
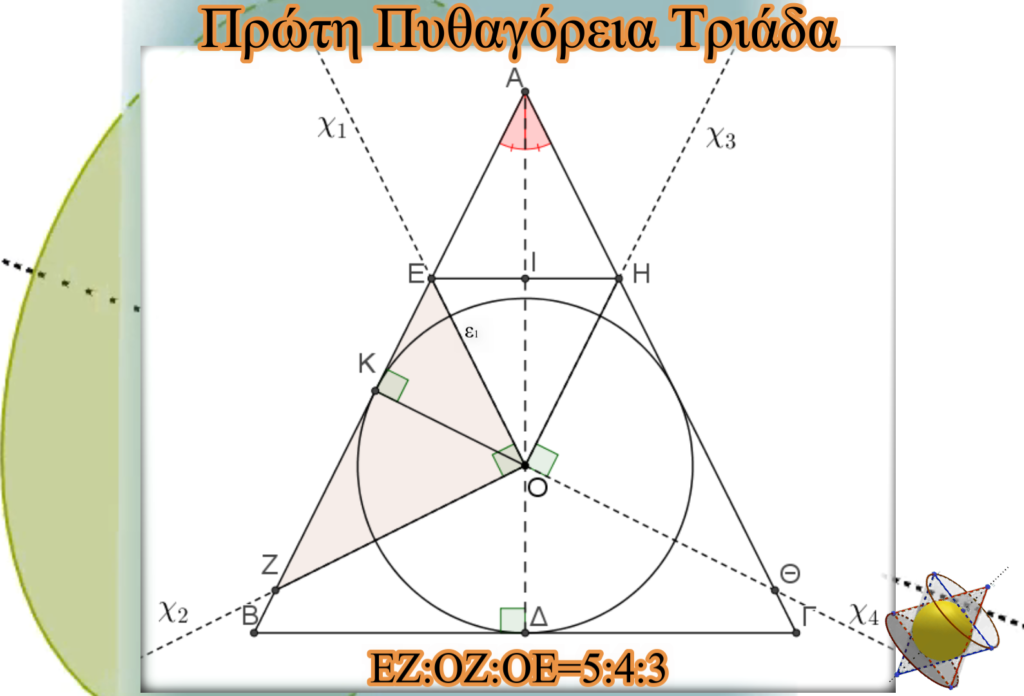
Οἱ ἀκτίνες Οχ1 καὶ Οχ2 τῆς Τετρακτύος τέμνουν τὴ πλευρὰ ΑΒ τοῦ χρυσοῦ τριγώνου στὰ σημεῖα Ε καὶ Ζ, σχηματίζοντας τὸ ΟΕΖ ὀρθογώνιο τρίγωνο . Τὸ τρίγωνο δὲν εἶναι τυχαῖο. Ἀποδεικνύεται (ἐδῶ) ὅτι ΕΟ=5/8, ΟΖ=5/6 και ΕΖ=25/24. Οἱ λόγοι τῶν πλευρῶν ποὺ προκύπτουν ἀκολουθοῦν τὴν πρώτη πυθαγόρεια τριάδα, δηλαδὴ οἱ μεταξὺ τους λόγοι ἔχουν τιμὲς 3:4:5. Οἱ πυθαγόρειες τριάδες εἶναι θετικοὶ ἀκέραιοι ἀριθμοὶ ποὺ ὑποστηρίζουν τὸ πυθαγόρειο θεώρημα. Ἐδῶ ἔχουμε 3²+4²=5².
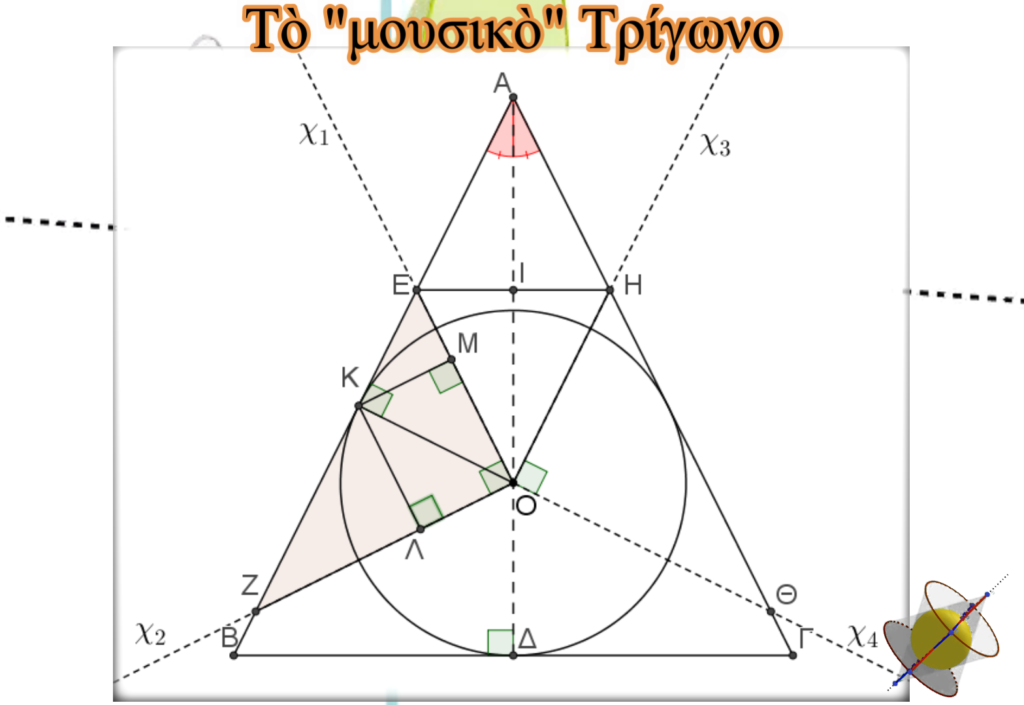
Ἀπὸ τὴν κορυφὴ Κ τοῦ ὀρθογωνίου τριγώνου ΚΟΖ φέρνουμε τὸ ὕψος ΚΛ πρὸς τὴν ὑποτείνουσα ΖΟ. Τὸ ἴδιο πράττουμε φέρνοντας καὶ τὸ ὕψος ΚΜ στὸ ὀρθογώνιο τρίγωνο ΚΟΕ. Φυσικὰ ὅλα τὰ νέα τρίγωνα εἶναι ὅμοια μὲ τὸ ἀρχικὸ ὀρθογώνιο τρίγωνο ΕΟΖ καὶ μὲ λόγους πλευρῶν 3:4:5.
Θὰ ὑπολογίσουμε τὰ μήκη τῶν πλευρῶν ποὺ μᾶς ἐνδιαφέρουν. Οἱ τιμὲς τῶν πλευρῶν που μᾶς ἐνδιαφἐρουν εἶναι ΚΛ=2/5, ΚΜ=3/10, ΖΛ=8/15 καὶ ΕΜ=9/10. Ὁ τρόπος ποὺ προκύπτουν φαίνεται ἐδῶ.
Τὰ εὐθύγραμμα τμήματα ποὺ ἐδῶ θὰ μᾶς ἀπασχολήσουν, θὰ τὰ τοποθετήσουμε στὴν πρώτη στήλη τοῦ πίνακα ποὺ ἀκολουθεῖ. Στὴν δεύτερη στήλη θὰ ἀναγράφονται τὰ ἀντίστοιχα μήκη τους, χρησιμοποιώντας μονάδα μέτρησης τὴ διάμετρο τοῦ ἐγγεγραμμένου κύκλου στὸ τρίγωνο ΑΒΓ ποὺ μᾶς ὑποδείχθηκε. Στὴ ἑπόμενη στήλη θὰ ἔχουμε τοὺς λόγους ὅλων τῶν εὐθύγραμμων τμημάτων σὲ σχέση μὲ τὸ ΟΚ , τὸ ὁποῖο εἶναι καὶ ἀκτίνα τοῦ κύκλου (ΟΚ=1/2). Θὰ θεωρήσουμε ὅτι ὅλα τὰ εὐθύγραμμα τμήματα εἶναι χορδὲς μὲ ἴδια χαρακτηριστικὰ (διατομή, ὑλικό, δύναμη κουρδίσματος), ἐκτὸς φυσικὰ τοῦ μήκους τους καὶ ὅτι πάλλονται δίνοντας ἤχους συγκεκριμένης συχνότητας. Ὅπως ἀναφέρθηκε, ἡ συχνότητα ποὺ παράγεται εἶναι ἀντιστρόφως ἀνάλογη τοῦ μήκους τῶν χορδῶν. Ἔτσι, θεωρώντας ὅτι ἡ χορδὴ ΟΚ παράγει τὴν νότα Ντό, στὰ 259,2 Hz μὲ ἀναφορὰ κουρδίσματος τὴν νότα Λὰ στὰ 432 Hz, θὰ βροῦμε ποιὲς νότες θὰ παρήγαγαν οἱ ὑπόλοιπες. Αὐτὲς φαίνονται στὴν ἑπόμενη στήλη. Στὴ συνέχεια καὶ ὅπου χρειάζεται, οἱ συχνότητες ποὺ προκύπτουν πολλαπλασιάζονται ἢ διαιροῦνται μὲ τὸν ἀριθμὸ 2 γιὰ νὰ βρεθοῦμε ἐντὸς τῶν ὁρίων τῆς μουσικῆς ὀκτάβας ποὺ ἀναφερόμαστε (259,2 Hz-518,4 Hz).
Στὶς ἑπόμενες στῆλες ἔχουμε τὶς κλίμακες Ντὸ ματζόρε καὶ Ντὸ μινόρε μὲ τὶς ἀναμενόμενες συχνότητες ποὺ ἡ θεωρία τῶν στάσιμων ἁρμονικῶν κυμάτων μᾶς ὑπέδειξε.
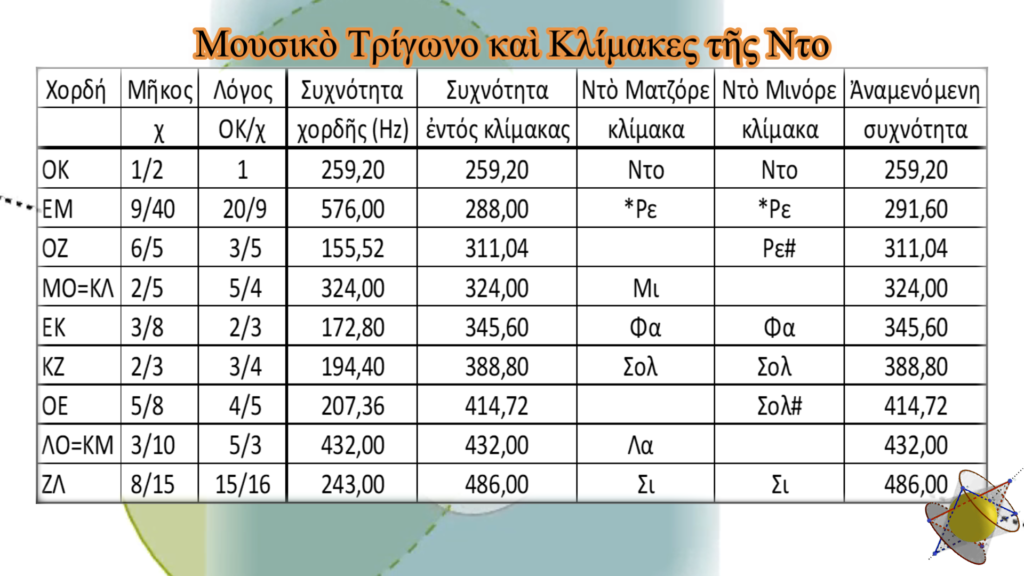
Τὸ ἀποτέλεσμα εἶναι ἐντυπωσιακό. Τὰ ἀναγραφόμενα στὸν πίνακα εὐθύγραμμα τμήματα, ποὺ ὁ συγκεκριμένος γεωμετρικὸς μηχανισμὸς μᾶς ἔδωσε, συμπεριφερόμενα σὰν χορδὲς μᾶς δίνουν ὅλες τὶς νότες ποὺ ὑπάρχουν στὶς κλίμακες τῆς Ντὸ ματζόρε καὶ Ντὸ μινόρε.
Ὑπάρχει ὅμως ἕνα μελανὸ σημεῖο. Ἡ συχνότητα γιὰ τὴν νότα Ρὲ ποὺ μᾶς δίνει τὸ γεωμετρικὸ σχῆμα (εὐθύγραμμο τμῆμα ΕΜ) δὲν ταυτίζεται μὲ τὴν συχνότητα τῆς Ρὲ ποὺ προκύπτει μὲ τὰ στάσιμα κύματα. Στὴν πρώτη περίπτωση ἐμφανίζεται ὁ μικρὸς τόνος (ΟΚ/ΕΜ=2·10/9), ἐνῶ ἐπιθυμητὸς εἶναι ὁ μεγάλος (Ρε/Ντο=9/8). Αὐτὸ ὅμως εἶναι ἀδυναμία τῆς μουσικῆς κλίμακας μὲ τὴν ἐμφάνιση δύο διαφορετικῶν τόνων. Ἐὰν τὸ παράδειγμα δίνονταν θεωρώντας πὼς ἡ χορδὴ ΟΚ παράγει τὴ νότα Σολ, τότε τὸ ΕΚ θὰ ἔδινε τὴ νότα Λά. Αὐτὴ τὴ φορὰ ὅμως ἡ τιμὴ θὰ ταυτίζονταν μὲ τὴ ζητούμενη, καθὼς ΛΑ/ΣΟΛ=(5/3 ΝΤΟ)/(3/2 ΝΤΟ)=10/9. Παρόλα αὐτὰ ἡ γεωμετρικὴ κατασκευὴ δὲν θὰ μποροῦσε νὰ μὴν δώσει καὶ τὸν μεγάλο τόνο.
Ὁ μεγάλος τόνος 9/8
Οἱ τέσσερις ἀπὸ κατασκευῆς ἀκτίνες τῆς Τετρακτύος τέμνουν τὸν ἐγγεγραμμένο κύκλο σὲ τέσσερα σημεῖα, τὰ ὁποία ὁρίζουν τὸ ἐγγεγραμμένο ἰσοσκελὲς τραπέζιο (ΠΡΣΤ). Μάλιστα ἀποδεικνύεται ὅτι ὁ λόγος τῶν βάσεων του εἶναι ἴσος μὲ 2.
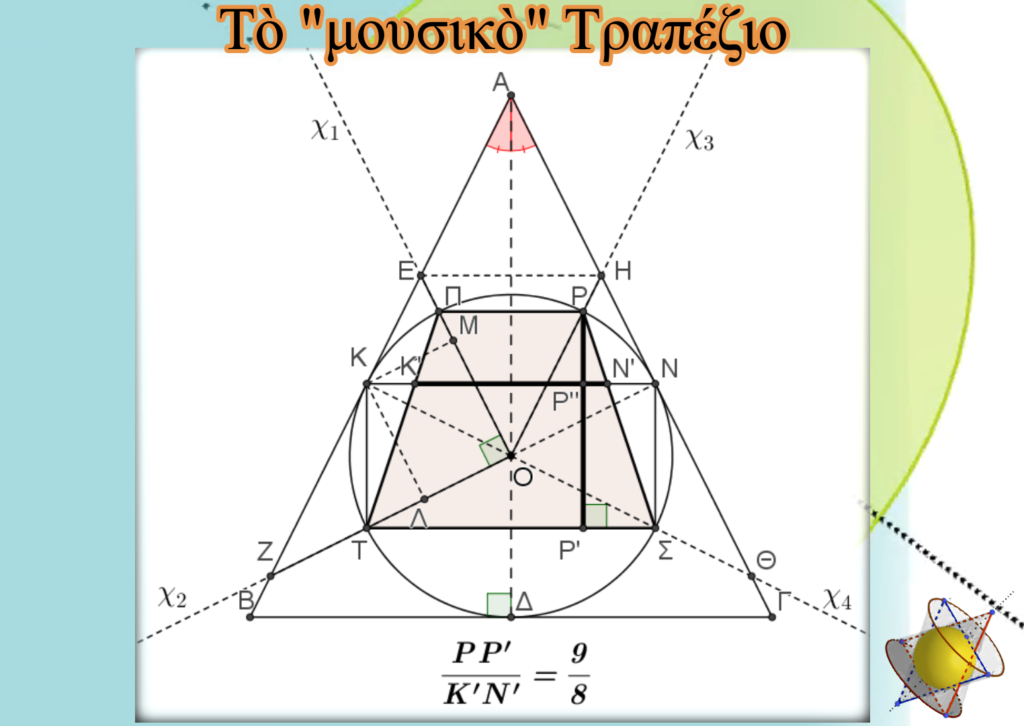
Τὰ σημεῖα Κ καὶ Ν στὰ ὁποία ὁ ἐγγεγραμμένος κύκλος ἐφάπτεται τῶν πλευρῶν τοῦ Χρυσοῦ τριγώνου, μᾶς δίνουν τὸ ΚΝ εὐθύγραμμο τμῆμα.
Αὐτό, τέμνει τὶς πλευρὲς τοῦ τραπεζίου στὰ σημεῖα Κ΄ καὶ Ν΄. Φέρνουμε καὶ τὸ ὕψος ΡΡ΄ τοῦ τραπεζίου (ΠΡΣΤ).
Ἀποδεικνύεται ὅτι . (ΡΡ΄)/(Κ΄Ν΄)=9/8
Οι μουσικοί λόγοι και οι τιμές τους σε μήκη ευθυγράμμων τμημάτων
Οἱ πλευρὲς τοῦ ὀρθογωνίου τριγώνου ΕΟΖ , ὅπως καὶ ὅλων τῶν ὁμοίων του, ἔχουν σχέση 5:4:3. Γιὰ ὅποια τιμὴ καὶ νὰ ἔχουν οἱ πλευρὲς του ἰσχύει ἡ σχέση:
(κ∙5)2=(κ∙4)2+(κ∙3)2
Σὰν βάση στοὺς ὑπολογισμοὺς χρησιμοποιήσαμε τὴν ἀκτίνα τοῦ μοναδιαίου κύκλου, τοῦ κύκλου δηλαδὴ ποὺ μᾶς δίνει ταυτόχρονα τὶς τιμὲς τῶν ἀριθμῶν π καὶ φ. Ἔτσι ὅλα τὰ εὐθύγραμμα τμήματα ποὺ προέκυψαν ἔχουν τιμὴ ἴση μὲ τὸ ½ τοῦ ἀντίστοιχου μουσικοῦ λόγου τους. Ὅπως εὔκολα μπορεῖ νὰ ἀποδειχθεῖ, ἡ γωνία ΟΕΖ τοῦ συγκεκριμένου ὀρθογωνίου τριγώνου εἶναι ἴση μὲ τὴν γωνία Α τῆς κορυφῆς τοῦ χρυσοῦ τριγώνου. Ἔτσι, αὐτόματα, τὸ ΑΝΖ ὀρθογώνιο τρίγωνο εἶναι ὅμοιο μὲ ὅλα τὰ προηγούμενα «μουσικὰ» τρίγωνα. Ὅπως ὅμως εἴδαμε, ΑΝ=ΑΚ=ΑΕ+ΕΟ=1
Γιὰ νὰ θεωρήσουμε ὅτι τὸ ΑΝ εὐθύγραμμο τμῆμα εἶναι τὸ ὕψος πρὸς τὴν ὑποτείνουσα ὅμοιου τριγώνου μὲ τὸ ΕΟΖ, ἀπὸ τὴν κορυφὴ Α φέρνουμε εὐθεία κάθετη στὴν ΑΒ, ἡ ὁποία τέμνει τὴν προέκταση τῆς ΖΝ στὸ σημεῖο Ξ. Ἔτσι τὸ ΑΞΝ «μουσικὸ» τρίγωνο ποὺ σχηματίστηκε, μαζὶ μὲ αὐτὰ ποὺ δημιουργοῦνται ἀπὸ τὰ ἐπιμέρους ὕψη ΝΧ καὶ ΝΨ, ἔχουν μήκη πλευρῶν μὲ τιμὲς ποὺ ἀντιστοιχοῦν στοὺς μουσικοὺς λόγους τῆς κλίμακας ματζόρε. Φυσικά, ἐὰν προστεθοῦν καὶ τὰ εὐθύγραμμα τμήματα ΑΖ καὶ ΑΞ, τότε προκύπτει καὶ ἡ κλίμακα μινόρε.
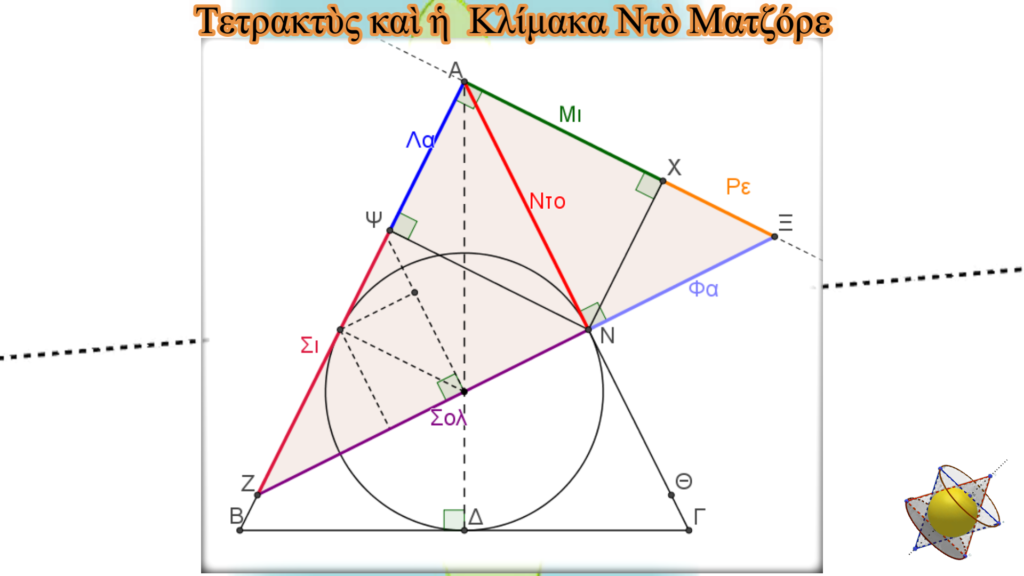
Ἐπειδή, οἱ διαστάσεις τοῦ συγκεκριμένου συμπλέγματος τριγώνων εἶναι διπλάσιες σὲ σχέση μὲ τὸ ἀρχικὰ δοσμένο, εἶναι σὰν νὰ περνᾶμε σὲ ἀπόδοση τὴ μουσικὴ κλίμακα στὴν ἑπόμενη ὀκτάβα. Οἱ διαδοχικὲς μεταβάσεις σὲ ὅμοια τρίγωνα διπλάσιων διαστάσεων καὶ ἑπομένως σὲ κλίμακες ἑπόμενης μουσικῆς ὀκτάβας, ἐπιτυγχάνεται μὲ ἕνα ἐνδιαφέροντα γεωμετρικὸ ἐξελικτικὸ μηχανισμὸ.
Βλέπουμε λοιπὸν τὸν συγκεκριμένο ἐλεγκτὴ συμβατότητας νὰ μᾶς δίνει τοὺς μουσικοὺς λόγους τῆς κλασσικῆς κλίμακας τόσο σὰν λόγους εὐθυγράμμων τμημάτων, ὅσο καὶ σὰν τιμές, σὰν μήκη δηλαδὴ εὐθυγράμμων τμημάτων. Ἔχοντας τὴν ἀποδοχὴ τῆς Τετρακτύος γιὰ τὴν ὕπαρξη καὶ ἑπομένως ἐφαρμογὴ τῶν δύο μουσικῶν κλιμάκων, γεννιοῦνται ἐρωτήματα. Ἔχουν μεταξὺ τους σχέση οἱ δύο μουσικὲς κλίμακες; Ἀφοῦ ἡ μουσικὴ εἶναι μία, γιατὶ νὰ ὑπάρχουν παραπάνω ἀπὸ μιὰ μουσικὲς θεωρίες; Τὴν ἀπάντηση στὴν πρώτη ἐρώτηση θὰ τὴν δοῦμε στὴν ἑπόμενη σελίδα. Ἡ ἀπάντηση στὴ δεύτερη, θὰ φανεῖ μὲ τὴ διαφορετικὴ ἐφαρμογὴ τους στὸ κοσμογονικὸ «μουσικὸ» μοντέλο τῆς Τετρακτύος ποὺ θὰ παρουσιαστεῖ στὴν 4η καὶ τελευταία ἑνότητα.

