Τετρακτύς
Τετρακτύς καὶ Χρυσὸ Τρίγωνο
Ἀπό τὸ βιβλίο…

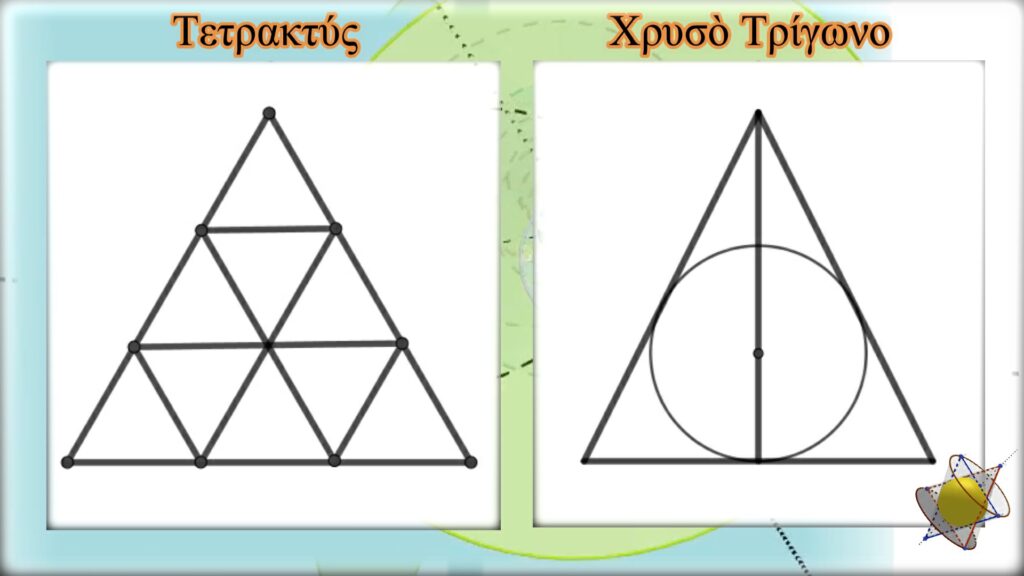
Στηριζόμενοι σὲ πηγὲς ποὺ ἔχουν διασωθεῖ ὡς τὶς μέρες μας, ἔχουμε ἀποδεχθεῖ πὼς ἡ μορφὴ τῆς Τετρακτύος εἶναι αὐτὴ τοῦ ἰσοπλεύρου τριγώνου καὶ ἔτσι, ἐπὶ αἰῶνες προσπαθούσαμε νὰ τὴν ἑρμηνεύσουμε, χωρὶς ὅμως νὰ μπορέσουμε νὰ ἀντλήσουμε τὶς προσδοκώμενες πληροφορίες ποὺ τὸ σύμβολο κρύβει, πέρα ἀπὸ κάποιες ἐλάχιστες.
Ὑπάρχει ὅμως καὶ ἕνα ἰδιαίτερο τρίγωνο ποὺ δείχνει νὰ ἔχει σχέση μὲ τὴν Τετρακτύν, ἕνα ἰσοσκελὲς τρίγωνο μὲ βάση ἴση μὲ τὸ ὕψος του. Τὸ ἀποκαλέσαμε Χρυσὸ Τρίγωνο γιατὶ περιέχει ὅλες τὶς ἀναλογίες τοῦ ἀριθμοῦ φ, χωρὶς αὐτὲς νὰ γίνονται ἄμεσα ἀντιληπτές. Δείξαμε ἐπίσης πὼς τὰ δύο τρίγωνα ἔχουν κάποια κοινὰ χαρακτηριστικὰ ποὺ τὰ συνδέουν . Ἡ ἀπορία ποὺ γεννᾶται εἶναι εὔλογη. Μήπως τὸ βασικὸ σχῆμα τῆς Τετρακτύος εἶναι αὐτὸ τοῦ Χρυσοῦ Τριγώνου, τὸ ὁποῖο ἁπλὰ μέσα στὸ πέρασμα τοῦ χρόνου παρερμηνεύτηκε ἢ ἀλλοιώθηκε;
Θὰ κάνουμε μιὰ συμφωνία.
Ἀπὸ τὴν πλευρὰ μου θὰ θεωρήσω πὼς τὸ Χρυσὸ Τρίγωνο εἶναι ἡ σχεδιαστική βάση τῆς Τετρακτύος. Γνωρίζοντας τὴν βαρύτητα τῆς δήλωσης αὐτῆς, ἡ ὁποία ἀνατρέπει τὰ ἕως σήμερα δεδομένα, καθὼς καὶ τὴν μεγάλη εὐθύνη τῆς ἀποκρυπτογράφησης τοῦ σημαντικώτερου ἴσος συμβόλου τῆς ἀρχαιότητας, θὰ σᾶς παρουσιάσω μέσα ἀπὸ τὴν ἀδιάψευστη γλώσσα τῶν μαθηματικῶν, ὅλους ἐκείνους τοῦ ἀριθμητικοὺς καὶ γεωμετρικοὺς λόγους στοὺς ὁποίους στηρίζονται οἱ γνωστὲς καὶ ὄχι μόνο μουσικὲς κλίμακες. Θὰ προσπαθήσω δηλαδὴ σὲ πρώτη φάση, νὰ ἐπαληθεύσω τὰ λόγια τοῦ Θέοντος τοῦ Σμυρναίου περὶ τῆς Τετρακτύος. Ἡ σχέση της μὲ τὸ Σύμπαν θὰ παρουσιαστεῖ καὶ θὰ ἀναλυθεῖ στὴν τέταρτη καὶ τελευταία ἑνότητα.
Ἀπὸ τὴν πλευρὰ σας, έφόσον ὅσα ἀναφερθοῦν τὰ βρεῖτε ἐνδιαφέροντα, ζητῶ νὰ τὰ ἀμφισβητήσετε, νὰ τὰ ἐλέγξετε, νὰ τὰ ἐρευνήσετε, ἔτσι ὥστε τεκμηριωμένα καὶ ὄχι δογματικὰ νὰ τὰ ἀποδεχθεῖτε ἢ νὰ τὰ ἀπορρίψετε.
Θὰ ξεκινήσουμε δεχόμενοι τὴν προτροπὴ τῆς ἴδιας τῆς λέξης «Τετρακτύς», τοποθετώντας στὸ Χρυσὸ Τρίγωνο τέσσερις συγκεκριμένες ἀκτίνες.
Κατασκευή
Ἀρχικὰ κατασκευάζουμε ἰσοσκελὲς τρίγωνο ΒΑΓ μὲ βάση ἴση μὲ τὸ ἀντίστοιχο ὕψος καὶ τὸν ἐγγεγραμμένο σὲ αὐτὸ κύκλο. Ὁρίζουμε σὰν μονάδα τὴν διάμετρο τοῦ κύκλου. Ἔτσι, αὐτόματα προκύπτει ὁ ἀριθμὸς φ ποὺ σὰν μέγεθος ἰσοῦται μὲ τὴ βάση καὶ τὸ ἀντίστοιχο ὕψος τοῦ τριγώνου, ἀλλὰ καὶ ὁ ἀριθμὸς π σὰν περίμετρος τοῦ μοναδιαίου κύκλου.
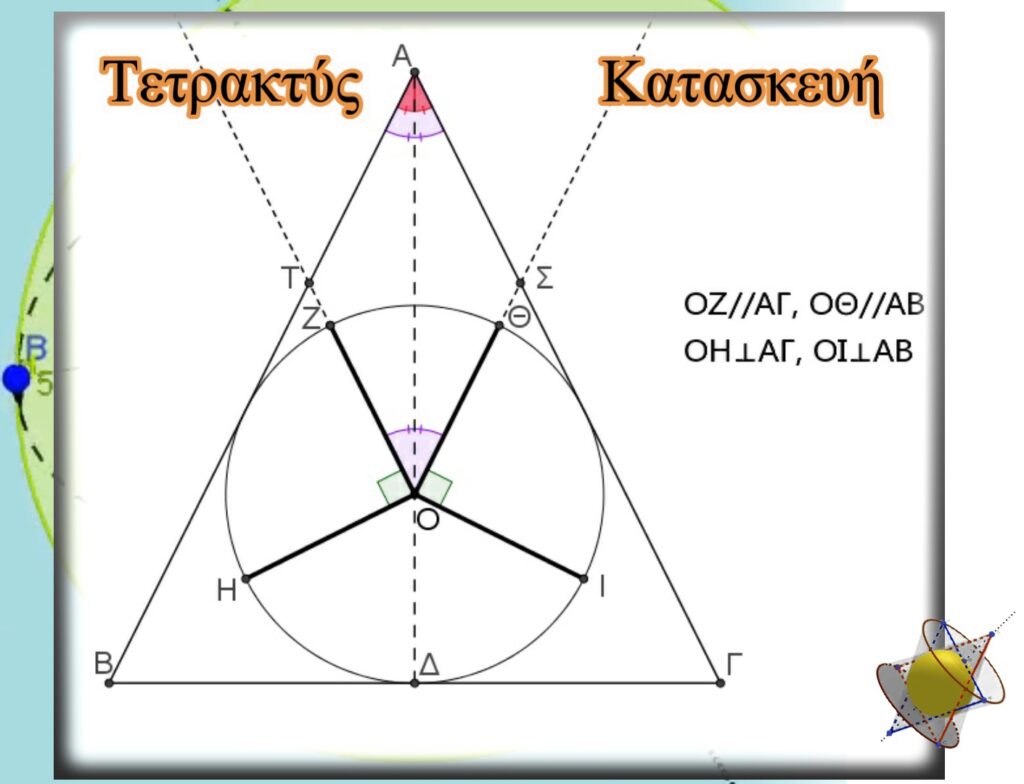
Σκοπὸς μας εἶναι νὰ φέρουμε τέσσερεις συγκεκριμένες ἀκτίνες, κατ’ ὑπόδειξη καὶ τῆς λέξης «Τετρακτύς», μὲ κορυφὴ τὸ κέντρο τοῦ μοναδιαίου κύκλου, τὸ ὁποῖο εἶναι ἐγγεγραμμένο στὸ Χρυσὸ Τρίγωνο. Αὐτὲς θὰ εἶναι ἡ ΟΖ ἀκτίνα, παράλληλη μὲ τὴν πλευρὰ ΑΓ, ἡ ΟΗ, κάθετη μὲ τὴ πλευρὰ ΑΓ καὶ ἀντίστοιχα οἱ ΟΘ καὶ ΟΙ. Ἔτσι σχηματίζονται οἱ ὀρθὲς γωνίες ΖΟΗ καὶ ΘΟΙ. Προεκτείνουμε τὶς ἀκτίνες ΟΖ καὶ ΟΘ. Οἱ ἡμιευθείες ποὺ σχηματίζονται τέμνουν τὶς πλευρὲς ΑΒ καὶ ΑΓ τοῦ τριγώνου στὰ σημεῖα Τ καὶ Σ ἀντίστοιχα. Τὸ τετράπλευρο (ΑΤΟΣ) ποὺ σχηματίζεται πέρα ἀπὸ παραλληλόγραμμο (ἀπέναντι πλευρὲς παράλληλες ἀπὸ κατασκευή), εἶναι καὶ ρόμβος (ἡ διαγώνιος ΑΟ διχοτομεῖ τὴν γωνία Α). Ἔτσι ΖΟ ̂Θ=ΒΑ ̂Γ σὰν ἀπέναντι γωνίες παραλληλογράμμου. Ἐπίσης καὶ ΗΟ ̂Ι=Β ̂+Γ ̂ γιατὶ
ΗΟ ̂Ι=360°-2∙90°-ΖΟ ̂Θ=180°-ΒΑ ̂Γ=Β ̂+Γ ̂
Ἂς δοῦμε τώρα τὰ πολὺ ἰδιαίτερα καὶ ἐνδιαφέροντα δεδομένα τῆς ἄνω κατασκευῆς μέσα ἀπὸ ἕνα «παιγνίδι» ἐμφάνισης ἀριθμητικῶν τιμῶν καὶ γεωμετρικῶν λόγων.

