Τετρακτύς
Πυραμιδολογία
Τὸ παράδοξο τοῦ μέτρου
Ἀπό τὸ βιβλίο…

Μάθαμε ὅτι τὸ μέτρο ὁρίστηκε σὰν μονάδα μέτρησης τοῦ μήκους ἀπὸ τὴν Ἀκαδημία τῶν Ἐπιστημῶν στὴ Γαλλία τὸ 1791. Ἀποφασίστηκε ὅτι αὐτὸ θὰ ἰσοῦται μὲ τὸ ἕνα δεκάκις ἑκατομμυριοστὸ τῆς ἀπόστασης ἀπὸ τὸν ἰσημερινὸ ἕως τὸν Βόρειο Πόλο καὶ μάλιστα μετρημένο ἀπὸ τὸν μεσημβρινὸ τῆς Γῆς ποὺ διασχίζει τὸ Παρίσι. Δόθηκε τὸ ὄνομα metre, γιὰ χάρη τῆς ἑλληνικῆς λέξης «μέτρον» καὶ τὸ ἀντίστοιχο ρῆμα «μετρῶ». Σχεδὸν ἕνα αἰώνα μετὰ ὑιοθετήθηκε ἀπὸ τὶς περισσότερες χῶρες.
Ἂς ἔλθουμε στὴν θέση τῶν ἐπιστημόνων, ποὺ θὰ ἀποφάσιζαν γιὰ τὴν πρότυπη μονάδα μέτρησης τοῦ βασικώτατου καὶ θεμελιώδους μεγέθους, τοῦ μήκους καὶ μάλιστα τὸ ἔτος 1791 μ.Χ. Κάποιος, ὀρθὰ θὰ πρότεινε νὰ χρησιμοποιηθεῖ μία ἀπὸ τὶς τότε ἰσχύουσες καὶ εὐρέως διαδεδομένες μονάδες μέτρησης, καθὼς ἔτσι θὰ γίνονταν πιὸ εὔκολα ἀποδεκτή. Κάποιος ἄλλος, ἐπίσης ὀρθά, θὰ πρότεινε μιὰ ἐντελῶς νέα μονάδα μέτρησης γιὰ νὰ ἀποφευχθοῦν τυχὼν ἀντιζηλίες μεταξὺ ἐθνοτήτων, περὶ πατρότητας της. Θὰ ἔπαιρναν ἔτσι τυχαία μιὰ βέργα εὐγενοῦς μετάλλου, ποὺ δὲν ὀξειδώνεται, γιὰ παράδειγμα χρυσοῦ, καὶ γιὰ ἀπόλυτα δεδομένη θερμοκρασία χώρου, θὰ τὴν ὁρίζανε σὰν πρότυπη μονάδα μέτρησης μήκους. Ἀντὶ αὐτῶν ὅμως, παρόλο ποὺ θὰ ἔπρεπε νὰ εἶναι ἀπόλυτοι ὡς πρὸς τὸ πρότυπο μέγεθος, προτίμησαν νὰ ὑιοθετήσουν πρὸς χρήση, μονάδα ποὺ ἀποτελεῖ ὑποδιαίρεση ἀπόστασης πλανητικῶν διαστάσεων, ποὺ καὶ γιὰ τὰ μέσα τῆς ἐποχῆς ἐκείνης, φαντάζει ἀπίστευτη ἡ δυνατότητα τῆς μέτρησής της μὲ ἀπόλυτη ἀκρίβεια.
Ἔτσι, ἱστορικὰ προέκυψε γιὰ πρώτη φορὰ τὸ μέτρο, σὰν συγκεκριμένο διάστημα καὶ αὐτὸ τὸ μέτρο χρησιμοποιήσαμε γιὰ τὶς μετρήσεις τῆς μεγάλης πυραμίδας.
Οἱ ἀρχαῖοι Αἰγύπτιοι, ὅπως εἶναι γνωστό, σὰν μονάδα μέτρησης χρησιμοποιοῦσαν τὸν Βασιλικὸ Πήχη, ὁ ὁποῖος, μετρημένος μὲ τὴν ἰσχύουσα μόλις τὰ τελευταία χρόνια μονάδα μέτρησης, δηλαδὴ τὸ μέτρο, εἶναι ἴσος μὲ 0,5236 μ.

Τὴν τιμὴ αὐτὴ ὅμως, τὴν ἔχουμε βρεῖ στὸ σχέδιο τοῦ μηχανισμοῦ ποὺ μᾶς ἔδωσε τὸν ἀριθμὸ π καὶ τὸν τετραγωνισμὸ τοῦ κύκλου. Ἐκεῖ, ἐὰν σὰν μονάδα μέτρησης παίρναμε τὴ διάμετρο τοῦ μοναδιαίου κύκλου καὶ τὴν ὁρίζαμε σὰν τὸ γνωστὸ μέτρο, ΑΒ=1 μέτρο , τότε θὰ βρίσκαμε ὅτι ἰσχύει:
ΓΚ=0,5236 μ.=1 ΒασιλικοςΠήχης
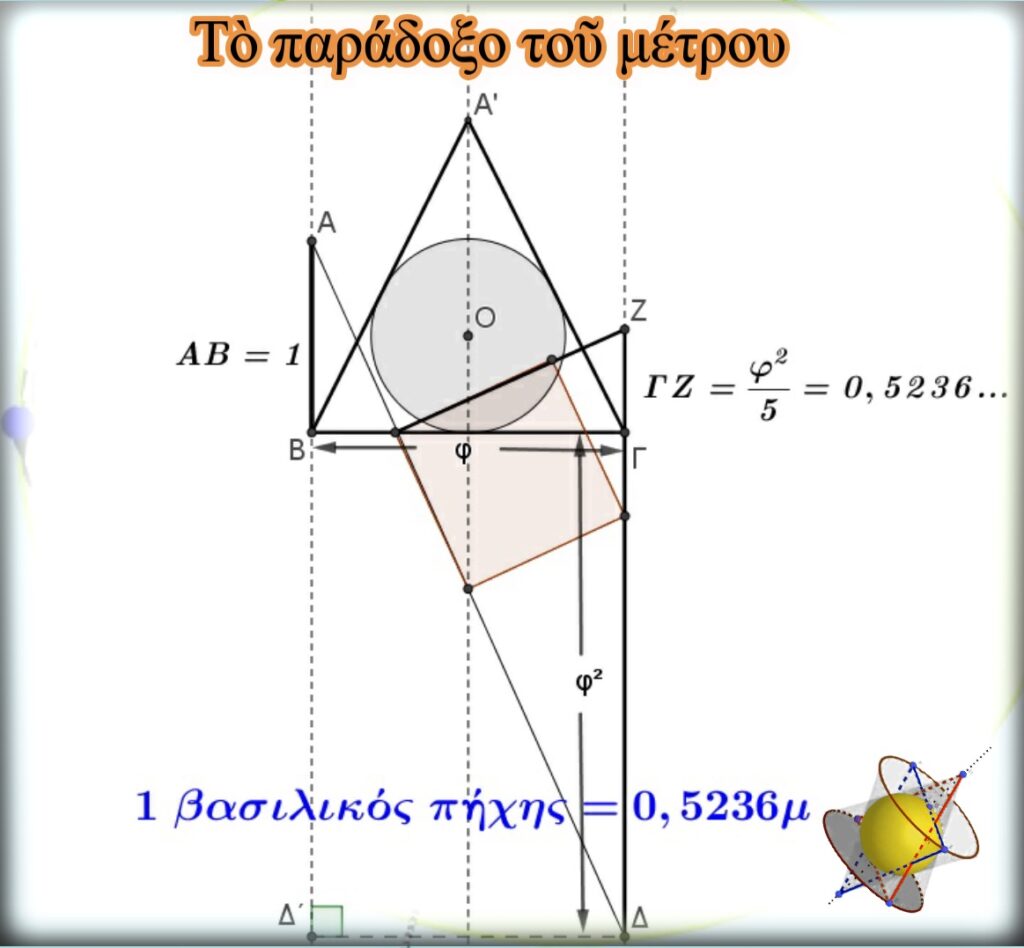
Δεχόμαστε ὅτι οἱ κατασκευαστὲς τῆς Μεγάλης πυραμίδας τὴν σχεδίασαν χρησιμοποιώντας τὸν συγκεκριμένο γεωμετρικὸ μηχανισμό, γιατὶ ἁπλὰ σχεδιασμὸς καὶ μηχανισμὸς ταυτίζονται. Ἄρα, ἐὰν θὰ εἶχαν σὰν μονάδα μέτρησης τὸν Βασιλικὸ Πήχη, τοὐλάχιστον θὰ γνώριζαν σὰν παράγωγη μονάδα τὸ μέτρο, μὲ τὴ σημερινή του διάσταση. Ἄλλωστε, τὸ μέτρο γιὰ τὸν δεδομένο μηχανισμό, ἰσοῦται μὲ τὴ διάμετρο τοῦ μοναδιαίου κύκλου, τοῦ ὁποίου ἡ περίμετρος ἰσοῦται μὲ τὸν ἀριθμὸ π. Ἐπίσης ἰσχύει: 6∙0,5236=π .
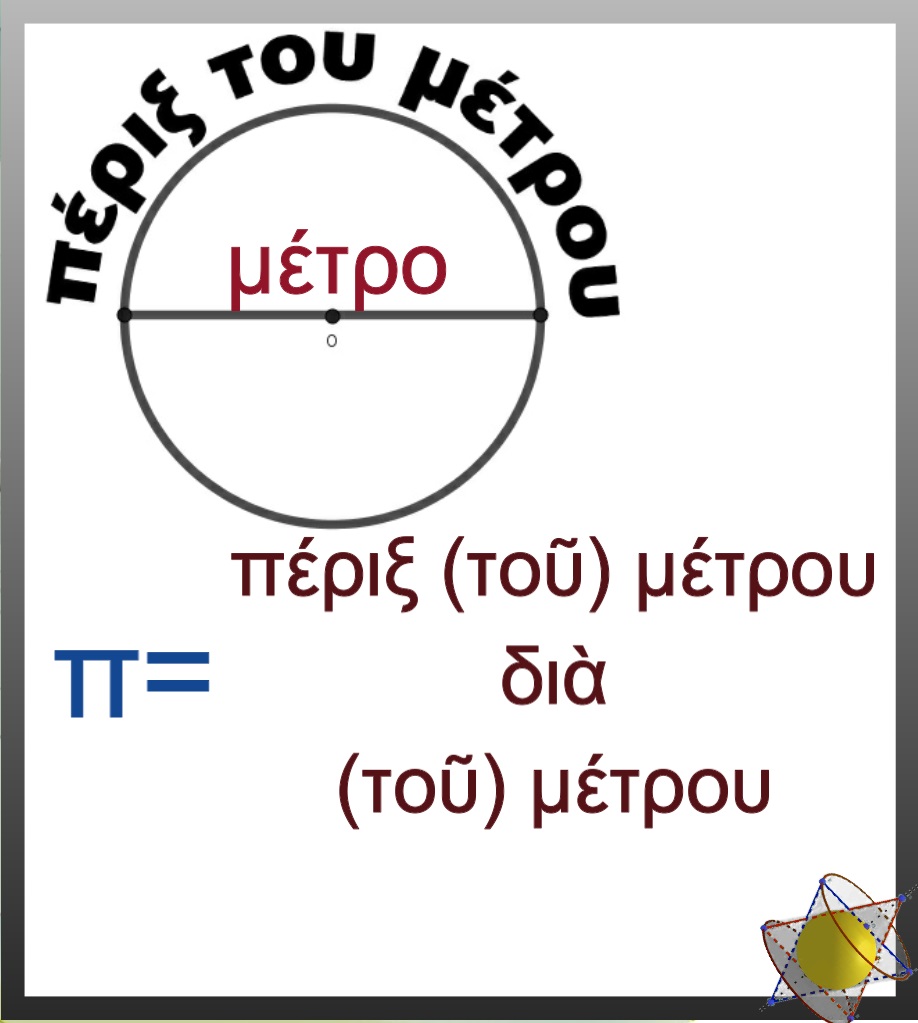
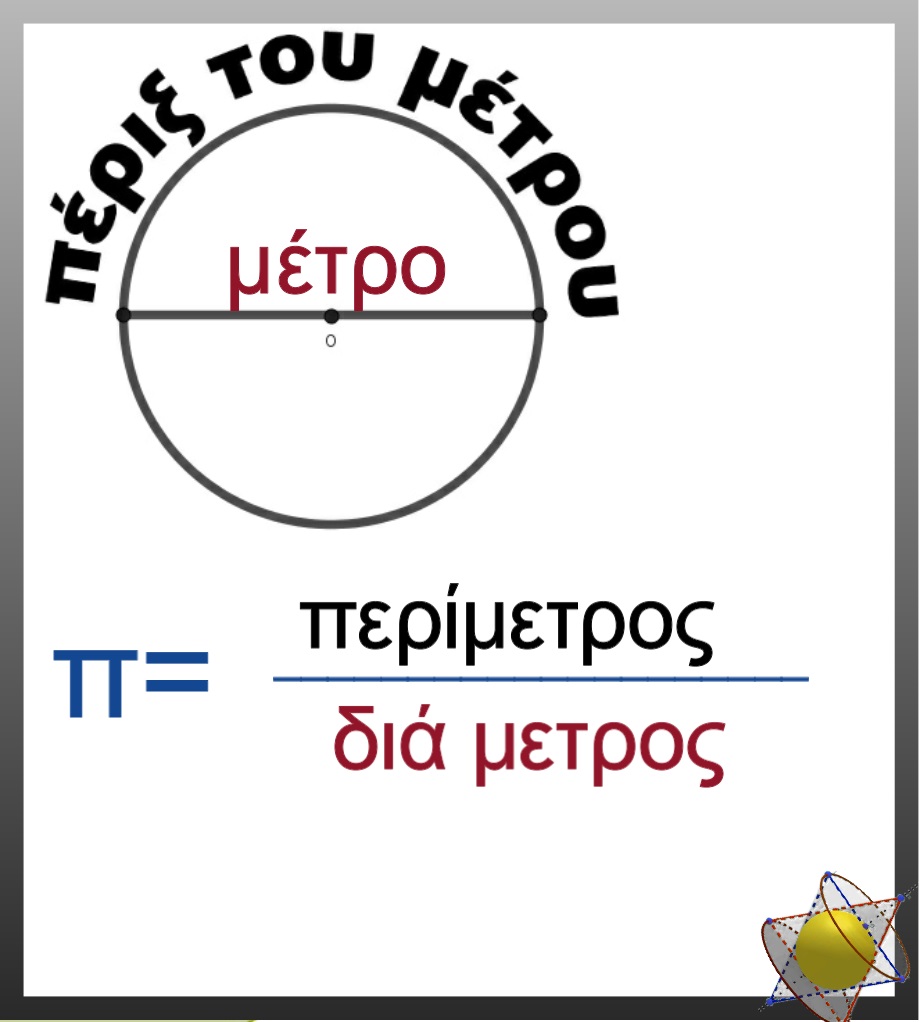
Ἂς ἀνέβουμε λίγο πιὸ βόρεια ἀπὸ τὴν Αἴγυπτο καὶ ἂς ἔρθουμε στὴν Ἑλλάδα. Εἶναι γνωστὸ τὸ πόσο δεικτικὴ ἦταν ἡ ἀρχαία ἑλληνικὴ γλώσσα καὶ πόσο προσπαθεῖ νὰ συνεχίσει νὰ εἶναι καὶ στὴ σημερινή της μορφή, παρὰ τὶς ἀλλοιώσεις ποὺ ὑφίσταται. Ὅπως εἴδαμε, γιὰ χάρη τῆς ἀρχαίας ἑλληνικῆς λέξης «μέτρον» δόθηκε τὸ ὄνομα metre στὴν μονάδα μήκους. Μά, οὔτε οἱ ἀρχαῖοι Ἕλληνες εἶχαν κάποια μονάδα μήκους μὲ αὐτὸ τὸ ὄνομα. Ἡ ἑλληνικὴ γλώσσα ὅμως, μᾶς δίνει ἄλλα στοιχεῖα. Μᾶς δίνει τὸν ὁρισμό, καθὼς καὶ τὸν τρόπο ὑπολογισμοῦ τοῦ ἀριθμοῦ π. Ὅπως γνωρίζουμε, ὁ ἀριθμὸς π ἰσοῦται μὲ τὴν περίμετρο τοῦ μοναδιαίου κύκλου διὰ τῆς διαμέτρου του, δηλαδὴ τῆς μονάδας. Ἂν θεωρήσουμε ὅτι κάποτε, στὴν ἀρχαία Ἑλλάδα, σὰν μονάδα μήκους εἶχαν τὸ μέτρο, τότε ὄντως ἡ λέξη περίμετρος θὰ δήλωνε «πέριξ τοῦ μέτρου» δηλαδὴ τὴν περίμετρο τοῦ κύκλου μὲ τὴν σημερινὴ ἔννοια. Ἐπίσης, ἡ λέξη διάμετρος, θὰ μᾶς ἔδινε τὴν πράξη τῆς διαίρεσης «διὰ-» καθὼς καὶ τὸν παρονομαστή, ποὺ εἶναι ἡ μονάδα μήκους τὸ «-μέτρο», στὸν ὑπολογισμὸ τοῦ ἀριθμοῦ π .
Τὰ πιὸ πάνω ἀναγραφόμενα εὔλογα δημιουργοῦν μεγάλη ἀμφιβολία, ὄχι γιὰ τὴν ὀρθότητα, ἀλλὰ γιὰ τὸ πόσο τυχαία καὶ αὐθαίρετη εἶναι ἡ ἐπιλογὴ τοῦ μέτρου σὰν πρότυπη μονάδα μέτρησης τοῦ μήκους. Ἐὰν τὸ μέτρο, σὰν μονάδα μήκους, ἦταν γνωστὸ ἀπὸ τὰ πανάρχαια χρόνια, τότε ἡ χρήση του κάπου θὰ ἀποσκοποῦσε ἢ μὲ κάποιο γενικώτερο σχέδιο θὰ ἐναρμονίζονταν. Φαντάζει πιθανό, οἱ σχεδιαστὲς τῆς μεγάλης πυραμίδας, μέσα ἀπὸ τὴν κατασκευή της, νὰ ἤθελαν καὶ τὴν μονάδα μέτρησης νὰ κάνουν γνωστή, ἀλλὰ καὶ νὰ ἐπιτύχουν τὸ σκοπὸ γιὰ τὸν ὁποῖο τὴν κατασκεύασαν, τηρώντας σχέσεις καὶ ἀναλογίες συνδεδεμένες τόσο μὲ τὴν Φύση καὶ τὸ Σύμπαν γενικώτερα, ὅσο καὶ μὲ τὴν Γῆ εἰδικώτερα.

