Ἡ μελοποιημένη ἀρχαία ἑλληνικὴ ποίηση
Φυσικὰ ἐξελικτικὰ φαινόμενα
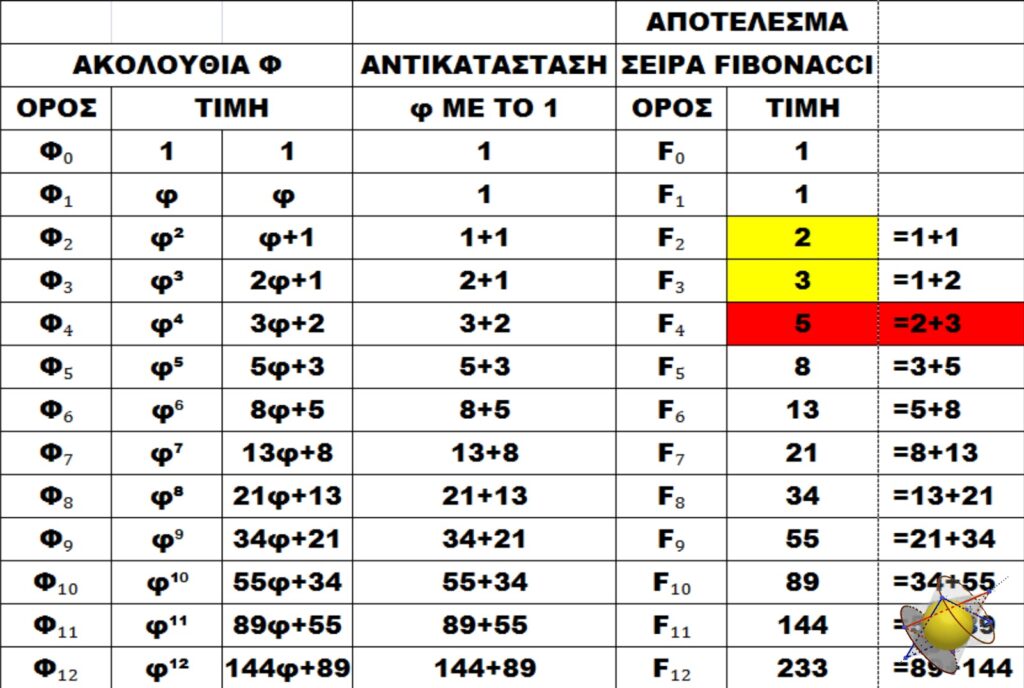
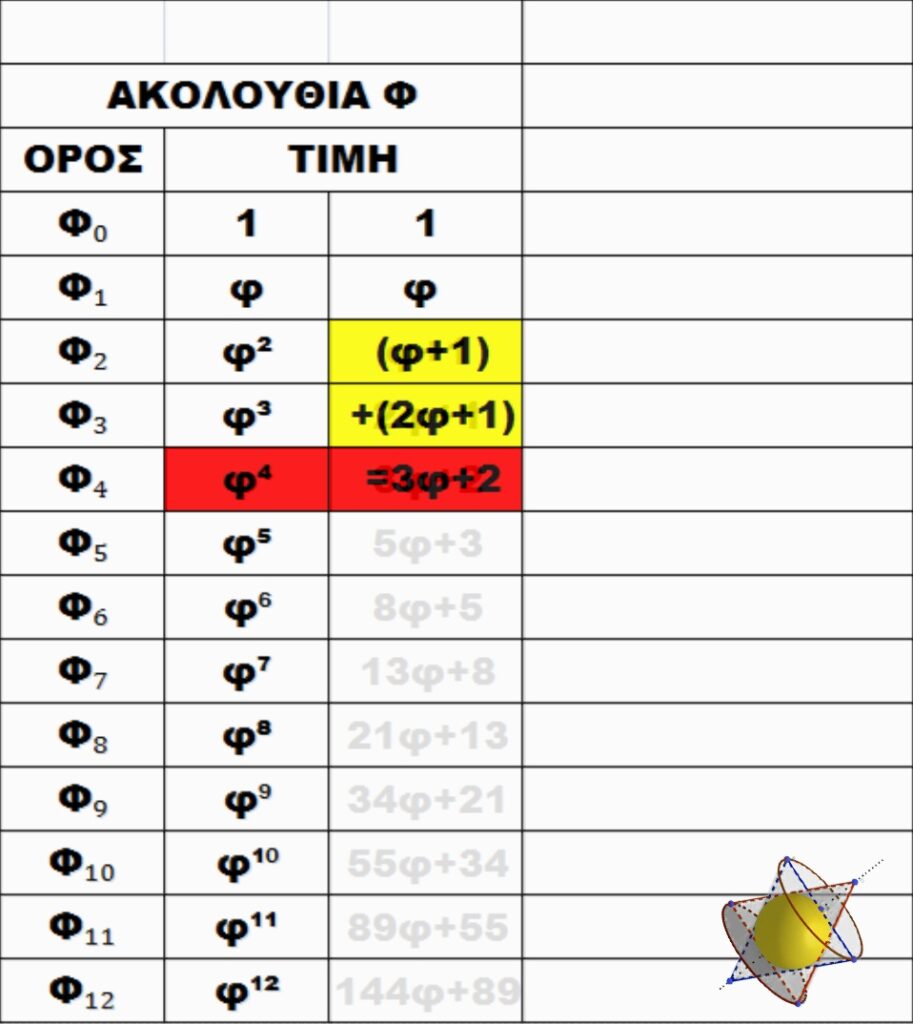
Ἡ ἀκολουθία φ εἶναι μιὰ γεωμετρικὴ πρόοδος ὅπου ὁ κάθε ἑπόμενος ὄρος τῆς προκύπτει μὲ πολλαπλασιασμὸ τοῦ προηγούμενου μὲ τὸν ἀριθμὸ φ. Ἔτσι, ὁ πρῶτος ὄρος τῆς ἀκολουθίας φ ἔχει τὴν τιμὴ ἕνα, ὁ δεύτερος τὴν τιμὴ φ, ὁ τρίτος ὄρος τὴν φ² κλπ.
Ἡ τιμή ὅμως τοῦ κάθε ἐπόμενου ὄρου τῆς ἀκολουθίας φ μπορεῖ νὰ προκύψη καὶ σὰν ἄθροισμα τῶν τιμῶν τῶν δύο προηγούμενων ὄρων. Ἔτσι ὁ τρίτος ὄρος μπορεῖ νὰ ἔχει τὴν μορφή ἀθροίσματος φ+1. Ἀντίστοιχα ὁ φ³ μπορεῖ νὰ πάρει τὴν τιμὴ (φ+1)+φ=2φ+1, ὁ φ⁴ τὴν τιμὴ (2φ+1)+(φ+1)=3φ+2 κ.τ.λ.
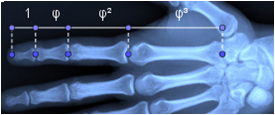
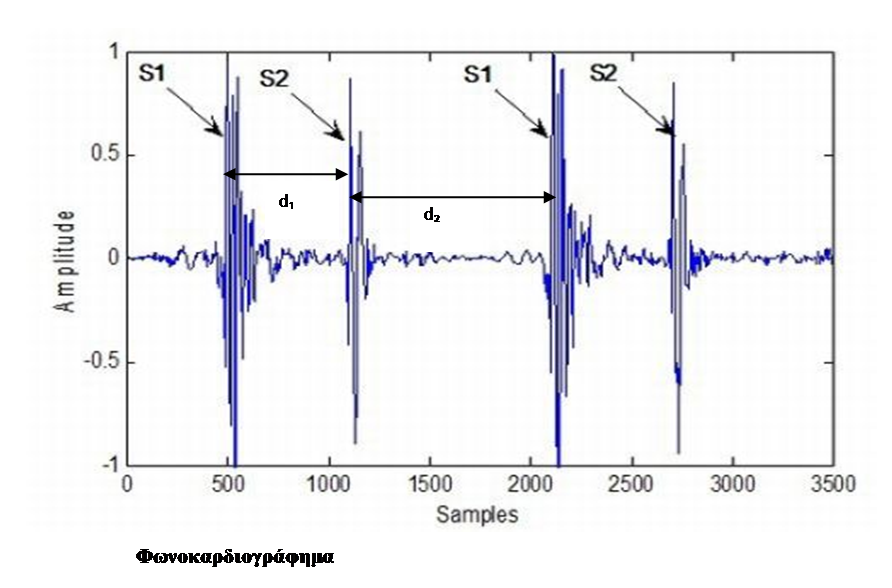
Αὐτὰ συμβαίνουν στὸν χῶρο τῶν μαθηματικῶν. Στὴ Φύση, ἡ ἀκολουθία Φ μπορεῖ νὰ ἑρμηνεύση ἕνα πλῆθος ἀπὸ φυσικὰ ἐξελικτικὰ φαινόμενα, ὅπως εἶναι τὰ μήκη τῶν φαλάγγων τῶν δακτύλων μας, ὅπως εἶναι οἱ χρόνοι ποὺ μεσολαβοῦν ἀνάμεσα στοὺς κτύπους τῆς καρδιᾶς μας.
Ἡ ἀκολουθία Φ, θὰ φανῆ στὴν συνέχεια πὼς ἔχει τὴν δυνατότητα νὰ ἐρμηνεύση τὸ μεγαλύτερο καὶ σημαντικότερο ἀπὸ ὅλα τὰ φυσικὰ ἐξελικτικὰ φαινόμενα, ποὺ εἶναι ἡ ἴδια ἡ δομὴ καὶ λειτουργία τοῦ Σύμπαντός μας.
Τί συμβαίνει ὅμως ὅταν τὰ μεγέθη ποὺ χαρακτηρίζουν συγκεκριμένα φυσικὰ ἐξελικτικὰ φαινόμενα θὰ πρέπει νὰ ἔχουν ἀκέραιες τιμές, ὅπως αὐτὸ συμβαίνει γιὰ παράδειγμα μὲ τὸν ἀριθμὸ τῶν κλαδιῶν ἑνὸς δέντρου ποὺ μετρούμε σὲ κάθε στάδιο ἀνάπτυξής του;
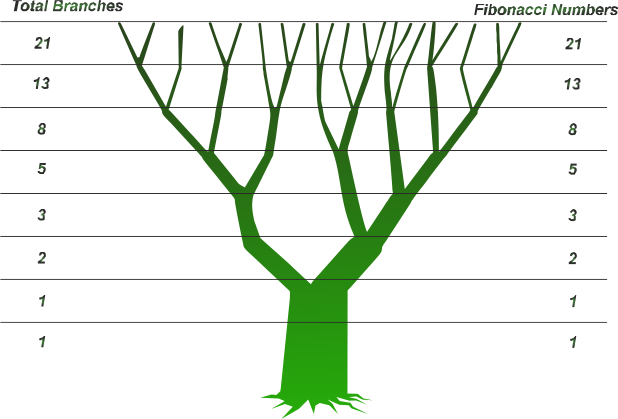
Σὲ αὐτὴν τὴν περίπτωση, ἡ ἀκολουθὶα φ προσαρμόζεται στὰ νέα δεδομένα καὶ ὁ ἀριθμὀς φ ἀπλῶς στρογγυλοποιεῖται παίρνοντας τὴν ἀμέσως μικρότερη ἀκέραια τιμή, τὴν μονάδα. Βέβαια, μὲ αὐτὸν τὸν τρόπο, κάθε φορὰ ἐμφανίζεται ἕνα ὑπόλοιπο. Τό ἔλλειμα, ποὺ σὲ κάθε περίπτωση μπορεῖ νὰ ἀναχθῆ σὲ ἐνεργειακὸ ἔλλειμα, εἶναι μόνο φαινομενικό. Εἶναι λογικό, τὸ σύστημα νὰ ἀποδέχεται ὅλη τὴν ἐνέργεια ποὺ κάθε φορὰ τοῦ προσφέρεται, ἡ μορφὴ τοῦ φαινομένου ὅμως εἶναι τέτοια ποὺ δὲν έπιτρέπει τό ἀποτέλεσμα νὰ φανῆ στὸ σύνολό του. Ἔτσι, τὸ ἐκάστοτε ἔλλειμα δὲν χάνεται, ἀντίθετα προστίθεται στὸ ἐπόμενο ἐξελικτικὸ στάδιο, δίνοντάς μας νέο ὑπόλοιπο καὶ ἡ διαδικασία αὐτὴ ἐπαναλαμβάνεται ὅσες φορὲς χρειαστεῑ, ἕως ὅτου τὸ φαινόμενο νὰ ὁλοκληρωθῆ.
Ἐὰν τώρα στὴν τελευταία στήλη τοῦ πίνακα ἐκτελέσουμε τὶς προσθέσεις, τότε ἔτσι ἁπλὰ θὰ προκύψη ἡ σειρὰ Fibonacci. Εἶναι σειρὰ μὲ ἀνάλογες ἰδιότητες μὲ αὐτὲς τῆς ἀκολουθίας φ. Καὶ στὴ σειρὰ Fibonacci, ὁ κάθε ὄρος της ἔχει τιμὴ ποὺ προκύπτει ἀπὸ τὸ ἄθροισμα τῶν τιμῶν τῶν δύο προηγούμενων ὄρων.
Πῶς μποροῦν νὰ συνεργαστοῦν μεταξὺ τούς, ἡ ἀκολουθία φ καὶ ἡ σειρὰ Fibonacci γιὰ νὰ προκύψουν μουσικοὶ ρυθμοί;