Ὁ τετραγωνισμὸς τοῦ κύκλου στὸ Πὶ καὶ Φί
Ἡ Χρυσὴ Τομή - Κατασκευή
Ἀπὸ τὸ βιβλίο…

Ἡ χρυσὴ τομή, ὅπως μᾶς τὸ λέει καὶ ἡ ἴδια ἡ φράση, εἶναι μία συγκεκριμένη τομὴ ἑνὸς εὐθυγράμμου τμήματος, ἡ ὁποία τὸ τέμνει, τὸ κόβει δηλαδὴ μὲ τέτοιο τρόπο, ἔτσι ὥστε ὁ λόγος τοῦ μεγαλύτερου εὐθυγράμμου τμήματος, πρὸς τὸ μικρότερο ἀπ’ αὐτὰ ποὺ δημιουργοῦνται, νὰ εἶναι ἴσος μὲ τὸν λόγο τοῦ ἀρχικοῦ εὐθυγράμμου τμήματος πρὸς τὸ μεγαλύτερο.
Ὁ λόγος αὐτὸς ἔχει ὄνομα, ἔχει καὶ τιμὴ. Τὸ ὄνομά του εἶναι «φ» καὶ ἡ τιμή του 1,618… 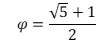

Κατασκευή
Ὑπάρχουν ἀρκετοὶ τρόποι εὕρεσης τῆς χρυσῆς τομῆς. Ἐδῶ θὰ δοῦμε αὐτὸν ποὺ πρωτοπαρουσίασα στὸ βιβλίο μου «γεωμετρικὲς κατασκευὲς στὸ πὶ καὶ φί», γιατὶ αὐτὰ ποὺ συνολικὰ θὰ προκύψουν ἔχουν τεράστιο ἐνδιαφέρον.
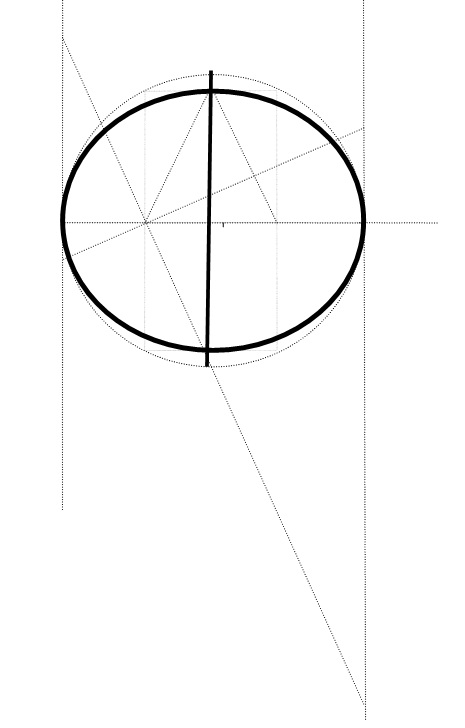
Πάνω σὲ εὐθεία ε, παίρνουμε τὸ εὐθύγραμμο τμῆμα ΒΓ, τοῦ ὁποίου τὴν χρυσὴ τομὴ θέλουμε νὰ βροῦμε.
Ἀφοῦ πρῶτα κατασκευάσουμε τὴν μεσοκάθετο αὐτοῦ, πάνω σὲ αὐτὴν παίρνουμε τὸ εὐθύγραμμο τμῆμα ΑΜ, τὸ ὁποῖο θὰ εἶναι ἴσο μὲ τὸ ΒΓ.
Ἔτσι σχηματίζεται ἕνα πολὺ ἰδιαίτερο ἰσοσκελὲς τρίγωνο, τὸ τρίγωνο ΑΒΓ τοῦ ὁποίου τὸ ὕψος πρὸς τὴ βάση του εἶναι ἴσο μὲ τὴ βάση του.
Στὴ συνέχεια κατασκευάζουμε τὸ ΔΜ εὐθύγραμμο τμῆμα, τὸ ὁποῖο θὰ εἶναι ἴσο μὲ τὸ ΑΒ καὶ τέλος τὸ ΒΕ εὐθύγραμμο τμῆμα, τὸ ὁποῖο θὰ εἶναι ἴσο μὲ τὸ ΔΒ.
Ἀποδεικνύεται (ἐδῶ) πὼς τὸ σημεῖο Ε ἀποτελεῖ τὴ χρυσὴ τομὴ τοῦ εὐθυγράμμου τμήματος ΒΓ.
Ὁ λόγος ποὺ κάνει σημαντικότατη τὴν προηγούμενη κατασκευὴ εἶναι ἡ ἐμφάνιση αὐτοῦ τοῦ ἰδιαίτερου ἰσοσκελοῦς τρίγωνου, τοῦ τριγώνου δηλαδὴ τοῦ ὁποίου τὸ ὕψος πρὸς τὴν βάση του εἶναι ἴσο μὲ τὴν βάση του. Σὲ αὐτό, ἂν καὶ δὲν φαίνονται, ὑπάρχουν μέσα του ὅλες αὐτὲς οἱ ἀναλογίες τῆς χρυσῆς τομῆς.
Γιὰ αὐτὸ καὶ τὸ συγκεκριμένο τρίγωνο τὸ ὀνόμασα χρυσὸ τρίγωνο.
Ἐὰν μάλιστα θεωρήσουμε ὅτι εἶναι ἴση μὲ τὴ μονάδα ἡ διάμετρος τοῦ ἐγγεγραμμένου σὲ αὐτὸ κύκλου, τότε ἀποδεικνύεται (ἐδῶ) πὼς ἡ βάση τοῦ τριγώνου εἶναι ἴση μὲ τὸν ἀριθμὸ φ, ἀλλὰ καὶ ἡ περίμετρος τοῦ κύκλου εἶναι ἴση μὲ τὸν ἀριθμὸ π.
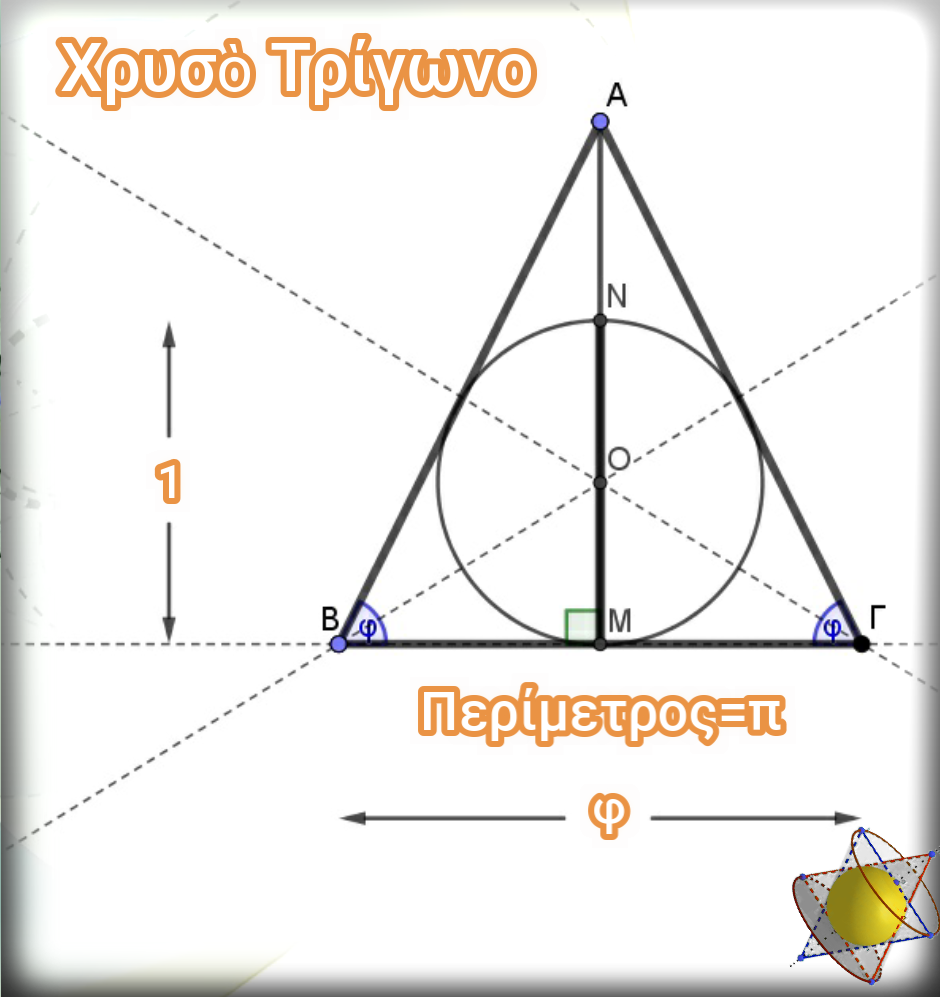
Εἶναι ἡ πρώτη φορά, ποὺ σ’ ἕνα τόσο ἁπλὸ γεωμετρικὸ σχῆμα, ἐμφανίζονται, μαζὶ μὲ τὴν μονάδα, ταυτόχρονα αὐτοὶ οἱ δύο σπουδαῖοι, αὐτοὶ οἱ δύο συμπαντικοὶ ὅπως θὰ φανεῖ ἀριθμοί, ὁ ἀριθμὸς π καὶ ὁ ἀριθμὸς φ, προϊδεάζοντας μας καὶ γιὰ τὴ μεταξὺ τους σχέση.

