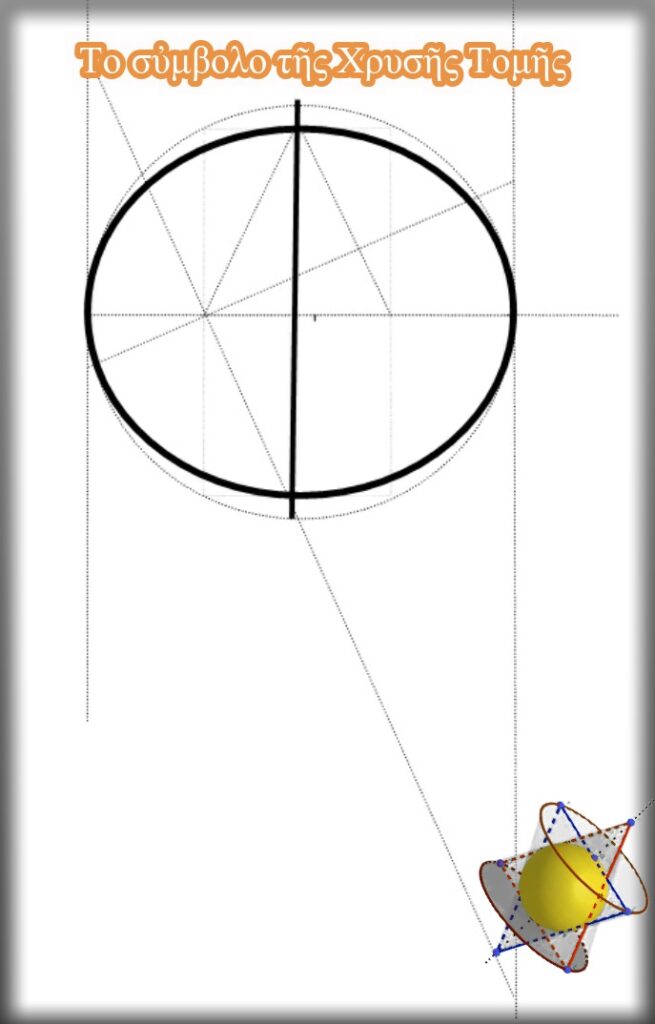
Ὁ τετραγωνισμὸς τοῦ κύκλου στὸ Πὶ καὶ Φί
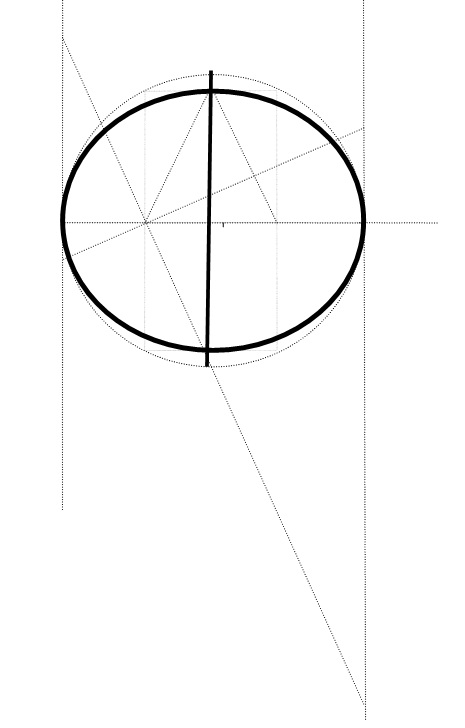
Χρυσὴ ἔλλειψη
Ἀπὸ τὸ βιβλίο…

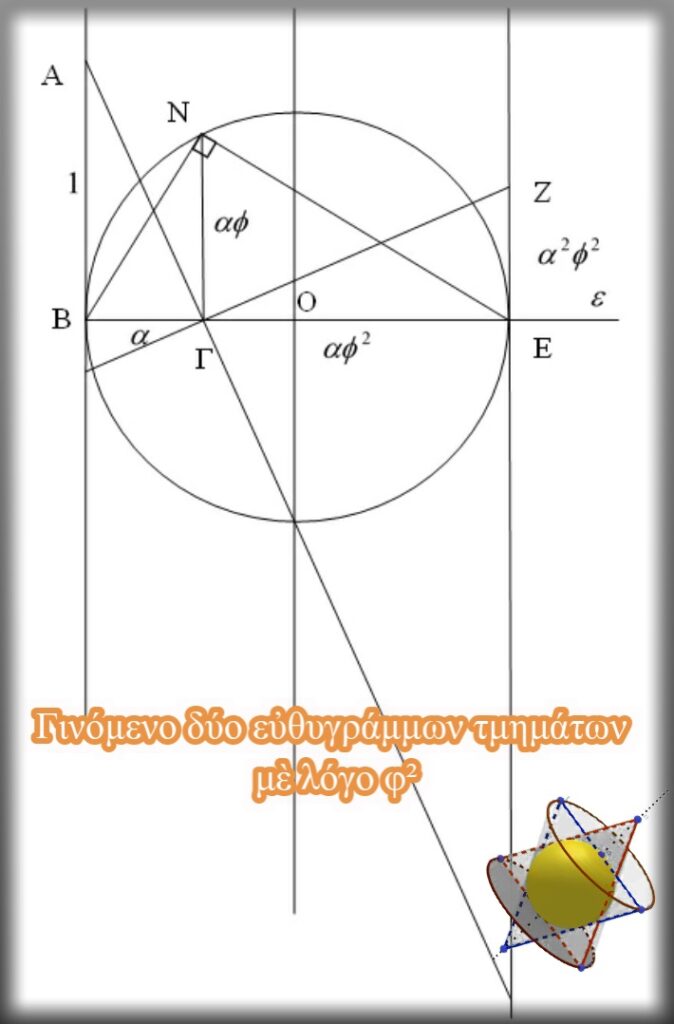
Ἔστω ὅτι ἔχουμε δύο εὐθύγραμμα τμήματα μὲ λόγο λ ἴσο μὲ τὸν ἀριθμὸ φ²=2,618. Ἔτσι ΒΓ=α καὶ ΓΕ=αφ² .
Ἂν τὰ ΒΓ καὶ ΓΕ εὐθύγραμμα τμήματα εἶναι συνεχόμενα σὲ εὐθεία ε καὶ τὸ ΒΑ εὐθύγραμμο τμῆμα εἶναι κάθετο στὴν εὐθεία ε καὶ ἴσο μὲ τὴν μονάδα, τότε τὸ εὐθύγραμμο τμῆμα ΕΖ ποὺ προκύπτει μὲ βάση τὸν γεωμετρικὸ μηχανισμὸ εὕρεσης τοῦ γινομένου δύο εὐθυγράμμων τμημάτων («ΓΕΩΜΕΤΡΙΚΕΣ ΚΑΤΑΣΚΕΥΕΣ ΣΤΟ Πὶ ΚΑΙ Φὶ» κεφ.1), θὰ ἰσοῦται μὲ τὸ γινόμενο τῶν ΒΓ καὶ ΓΕ δηλαδὴ : ΕΖ=ΒΓ·ΓΕ=α(αφ²)=(αφ)²
Ἀλλὰ καὶ τὸ ὕψος ΓΝ πρὸς τὴν ὑποτείνουσα τοῦ ὀρθογωνίου τριγώνου ΒΕΝ ἰσοῦται μὲ αφ.
Ἑπομένως ΕΖ=ΓΝ² .
Ἄρα ΤΟ ΓΝ ΕΙΝΑΙ Ὁ ΓΕΩΜΕΤΡΙΚΟΣ ΜΕΣΟΣ ΤΩΝ ΒΓ ΚΑΙ ΓΕ ΜΕ ΛΟΓΟ Φ (ΒΓ·ΓΕ=ΕΖ=ΓΝ²), καὶ τὸ σημεῖο N εἶναι σημεῖο τῆς περιμέτρου κύκλου μὲ κέντρο O τὸ μέσον τῆς διαμέτρου του ΒΕ.
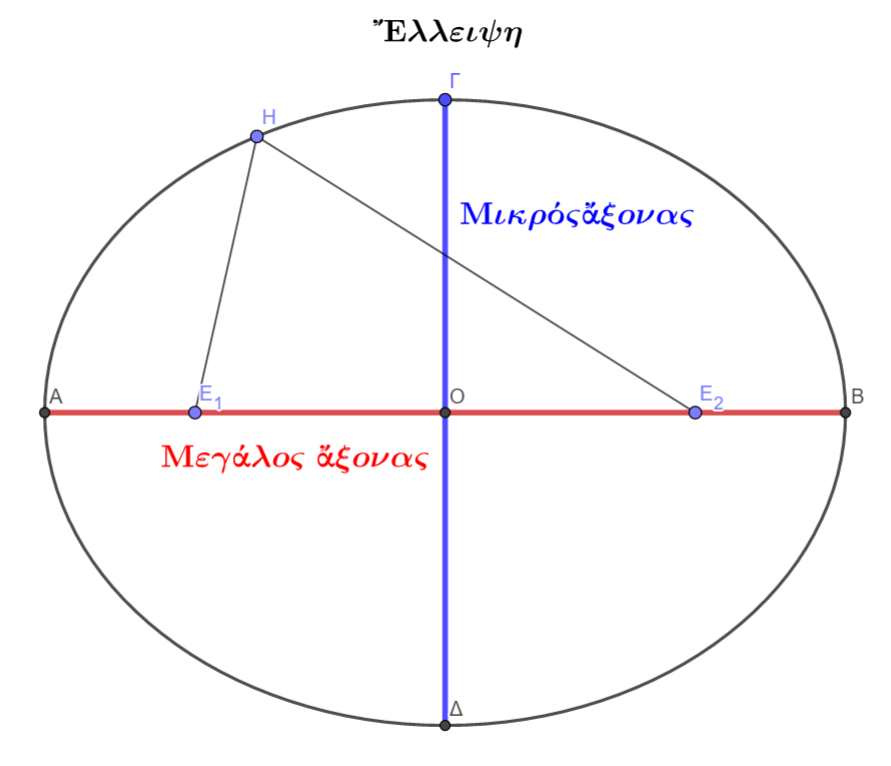
Ὁρισμός ἔλλειψης
Ἔλλειψη ὀνομάζεται ὁ γεωμετρικὸς τόπος (τὸ σύνολο) τῶν σημείων ἑνὸς ἐπιπέδου τῶν ὁποίων τὸ ἄθροισμα τῶν ἀποστάσεων ἀπὸ δύο σημεῖα τοῦ ἐπιπέδου εἶναι σταθερὸ καὶ ἰσοῦται μὲ τὸν μεγάλο ἄξονα τῆς ἔλλειψης.
Δύο συνεχόμενα σὲ εὐθεία εὐθύγραμμα τμήματα μποροῦν νὰ ὁρίσουν ἀπόλυτα μία ἔλλειψη μὲ μεγάλο ἄξονα ἴσο μὲ τὸ ἄθροισμα τῶν δύο εὐθυγράμμων τμημάτων καὶ μικρὸ ἄξονα ἴσο μὲ τὸ διπλάσιο τῆς τετραγωνικῆς ρίζας τοῦ γινομένου τους («ΓΕΩΜΕΤΡΙΚΕΣ ΚΑΤΑΣΚΕΥΕΣ ΣΤΟ Πὶ ΚΑΙ Φὶ» κεφ.2). Ἄρα, στὴν συγκεκριμένη περίπτωση, ἂν ἀπὸ τὸ σημεῖο Ο φέρουμε κάθετη στὴν εὐθεία ε καὶ ὁρίσουμε τὸ ΟΘ εὐθύγραμμο τμῆμα ἴσο μὲ τὸ ΟΘ΄ εὐθύγραμμο τμῆμα , ἴσο μὲ τὸ ΓΝ , τότε ἔχουμε ὁρίσει ἔλλειψη μὲ μεγάλο ἄξονα τὸ ΒΕ εὐθύγραμμο τμῆμα, μικρὸ ἄξονα τὸ ΘΘ΄ καὶ ἑστίες τῆς ἔλλειψης τὰ σημεῖα Γ καὶ Γ΄ ὅπου ΒΓ=Γ΄Ε.
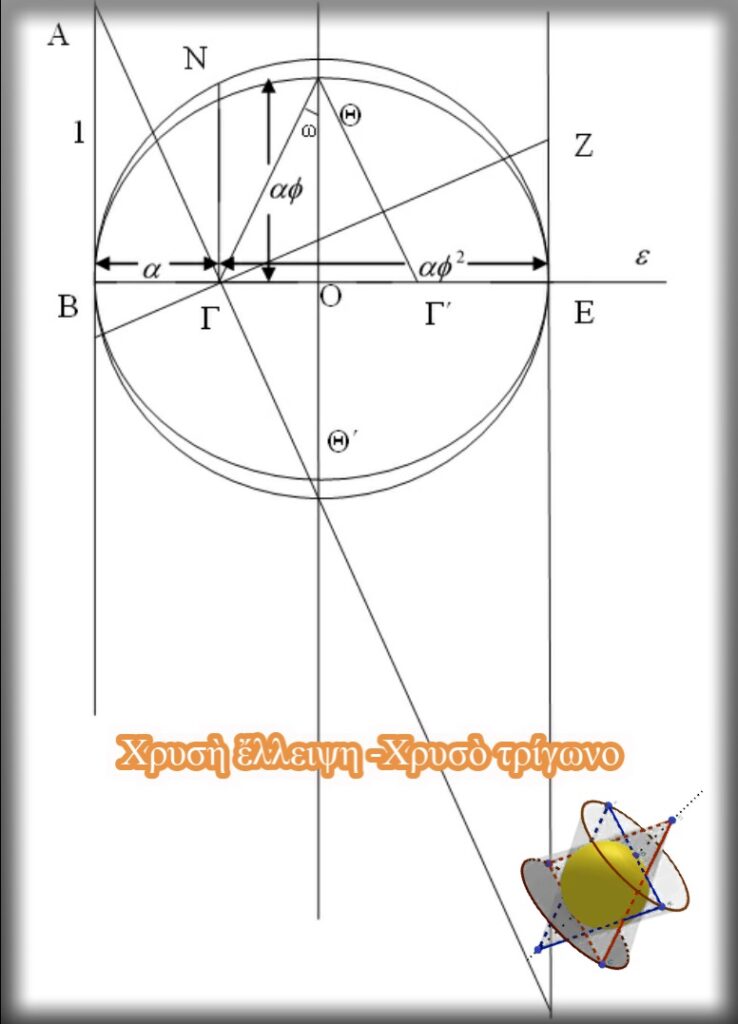
Ἀποδεικνύεται ὅτι ἡ ἀπόσταση τῶν δύο ἑστιῶν τῆς ἔλλειψης ἰσοῦται μὲ τὸ ΟΘ εὐθύγραμμο τμῆμα. ΓΓ΄=ΟΘ
ΓΓ΄=ΓΕ-ΓΈ=ΓΕ-ΒΓ=αφ²-α=α(φ²-1)=αφ=ΟΘ
Δηλαδὴ ἡ ἑστιακὴ ἀπόσταση ΓΓ΄τῆς συγκεκριμένης ἔλλειψης εἶναι ὁ γεωμετρικὸς μέσος τῶν ΒΓ καὶ ΓΕ εὐθυγράμμων τμημάτων , ποὺ ὁρίζουν τὴν ἔλλειψη, μὲ λόγο τὸν ἀριθμὸ φ.
Ἀποδεικνύεται ἐπίσης ὅτι τὸ ΓΘ εὐθύγραμμο τμῆμα ἰσοῦται μὲ τὴν ἀκτίνα τοῦ κύκλου διαμέτρου ΒΓ.
Ἀπὸ τὶς παραπάνω σχέσεις προκύπτει πὼς τὸ ὕψος ΘΟ τοῦ ἰσοσκελοῦς τρίγωνο ΓΘΓ΄, ποὺ σχηματίζεται στὴν συγκεκριμένη ἔλλειψη, εἶναι ἴσο μὲ τὴ βάση του ΓΓ΄, δηλαδὴ τῆς ἀπόστασης τῶν δύο ἑστιῶν τῆς ἔλλειψης καὶ μάλιστα εἶναι καὶ ὁ γεωμετρικὸς μέσος τῶν ΒΓ καὶ ΓΕ εὐθυγράμμων τμημάτων. (Ἐμφάνιση τοῦ ΧΡΥΣΟΥ ΤΡΙΓΩΝΟΥ)
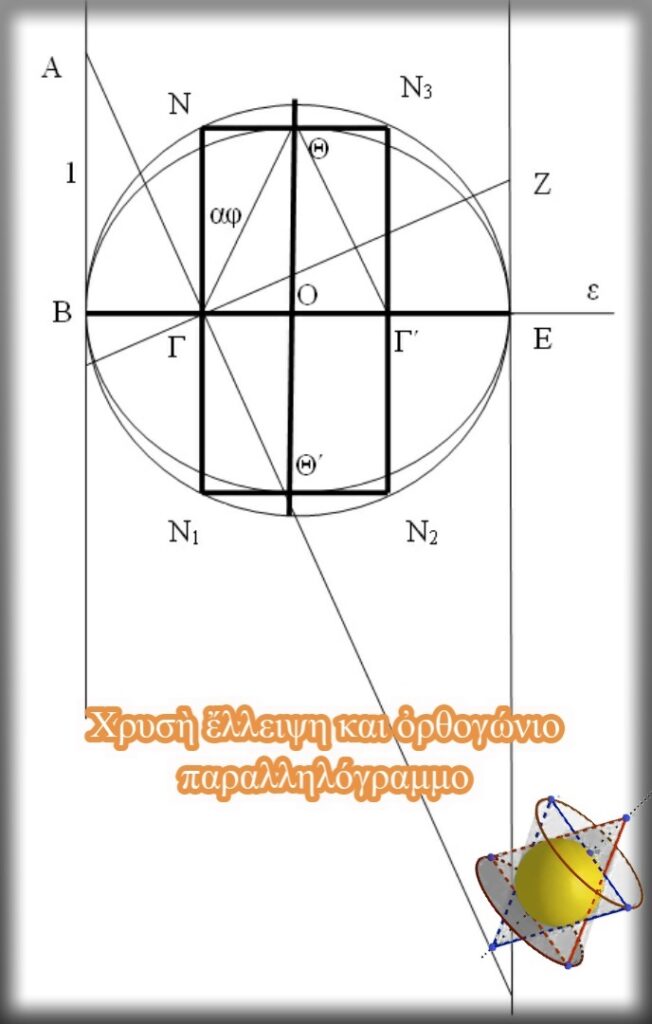
Προεκτείνουμε τὴν ΓΝ ἡ ὁποία τέμνει τὸν κύκλο (Ο,ΟΒ) στὸ σημεῖο Ν1.
Ἀπὸ τὸ σημεῖο Γ΄ φέρνουμε εὐθεία κάθετη στὴν εὐθεία ε ἡ ὁποία ἐπίσης τέμνει τὸν κύκλο στὰ σημεῖα Ν2 καὶ Ν3. Τὸ ὀρθογώνιο παραλληλόγραμμο ΝΝ1Ν2Ν3 ποὺ σχηματίζεται ἔχει ἀναλογίες 2:1 καὶ σαφῶς μᾶς θυμίζει τὴν συνηθέστερη μέθοδο εὕρεσης τῆς χρυσῆς τομῆς εὐθύγραμμου τμήματος.
Ἐπίσης ὁ λόγος τοῦ μεγάλου ἄξονα τῆς ἔλλειψης (διάμετρος τοῦ μεγάλου κύκλου) πρὸς τὸν μικρὸ ἄξονα ἔλλειψης εἶναι σταθερὸς καὶ ἴσος μὲ: α(φ²+1)/2αφ=√5/2=1,118… ἀριθμὸς ὁ ὁποῖος προκύπτει καὶ μὲ τὴν διαίρεση τῆς ἀκτίνας τοῦ κύκλου μὲ τὴ μικρὴ πλευρὰ τοῦ ὀρθογωνίου παραλληλογράμμου.
Ἁπλὴ ἀναφορὰ γίνεται στοὺς λόγους αὐτοὺς 2:1:1,118 γιατὶ σὰν ἀναλογίες μήκους, πλάτους, ὕψους ἔχουν συναντηθεῖ σὲ ἀρχαῖες καὶ ὄχι μόνο κατασκευὲς ποὺ κατὰ καιροὺς ἀπασχόλησαν διάφορους ἐρευνητὲς (τὸ διαμέρισμα τοῦ Βασιλιὰ στὴν μεγάλη πυραμίδα τοῦ Χέοπα, ὁ καθεδρικὸς ναὸς τοῦ Σαρτρ).
– Εὔκολα ἀποδεικνύεται πὼς καὶ ὁ λόγος τοῦ ἐμβαδοῦ τοῦ κύκλου μὲ διάμετρο ἴση μὲ τὸν μεγάλο ἄξονα τῆς ἔλλειψης πρὸς τὸ ἐμβαδὸν τῆς ἔλλειψης ἰσοῦται μὲ √5/2=1,118…
– Τὸ σημεῖο Γ ἀποτελεῖ τὴ χρυσὴ τομὴ τοῦ ΒΓ΄ διότι ΒΓ=α καὶ ΓΓ΄=αφ, ὁμοίως καὶ τὸ σημεῖο Γ΄ εἶναι ἡ χρυσὴ τομὴ τοῦ ΓΕ .
Συνοψίζοντας ὅλες αὐτὲς τὶς ξεχωριστὲς ἰδιότητες θὰ μπορούσαμε νὰ χαρακτηρίσουμε σὰν ΧΡΥΣΗ ΕΛΛΕΙΨΗ κάθε ἔλλειψη ποὺ ὁρίζεται ἀπὸ δύο συνεχόμενα εὐθύγραμμα τμήματα μὲ λόγο λ=φ².
Ἐπίσης θὰ μπορούσαμε νὰ χαρακτηρίσουμε καὶ ΧΡΥΣΟ ΤΡΙΓΩΝΟ κάθε ἰσοσκελὲς τρίγωνο τοῦ ὁποίου ἡ βάση του εἶναι ἴση μὲ τὸ ὕψος τοῦ τριγώνου ἀπὸ τὴν κορυφὴ του, καὶ αὐτὸ διότι ἂν καὶ δὲν φαίνεται, μέσα σὲ αὐτὸ «κρύβονται» ὅπως εἴδαμε ὅλα τὰ εὐθύγραμμα τμήματα μὲ ἀναλογίες ἴσες με τὸν ἀριθμὸ φ.
Κάτι τελευταῖο.
Μὲ ἁπλὴ παρατήρηση βλέπουμε τὴν περιφέρεια τῆς ἔλλειψης μαζὶ μὲ τὴν κάθετη διάμετρο τοῦ κύκλου νὰ σχηματίζουν τὸ γράμμα Φ. Εἶναι τὸ ἴδιο τὸ γράμμα, τὸ ὁποῖο σὰν σύμβολο περιέχει μέσα του τὴν ἀπάντηση γιὰ τὶς μοναδικὲς ἰδιότητες του.