Ὁ τετραγωνισμὸς τοῦ κύκλου στὸ Πὶ καὶ Φί
Ἡ ἀκολουθία Φν
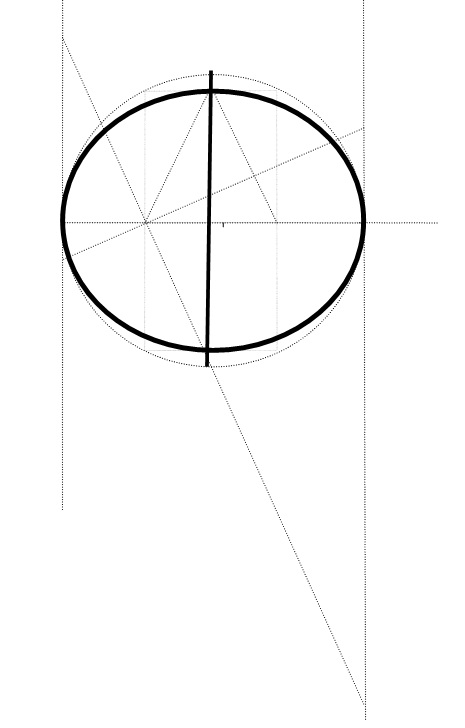
Ἀπό τὸ βιβλίο…

Τὸ φλὲρτ τῆς ἀκολουθίας Φν μὲ τοὺς ἀκεραίους
Ἡ ἀκολουθία τοῦ ἀριθμοῦ φ εἶναι μία γεωμετρικὴ πρόοδος μὲ λόγο λ τὸν ἀριθμὸ φ, ὅπου: 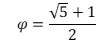
Ἔτσι, γιὰ τιμὲς τοῦ ν ἀπὸ τὸ -∞ ἕως τὸ +∞ ἔχουμε: Φν=λ·Φν-1=φ·φν-1=φν.
Σὲ ἕνα ὑπολογιστικὸ φύλλο δημιουργοῦμε τὸν ἑπόμενο πίνακα γιὰ τιμὲς τοῦ ἀκεραίου ἀριθμοῦ ν ἀπὸ τὸ -12 ἕως τὸ 24.
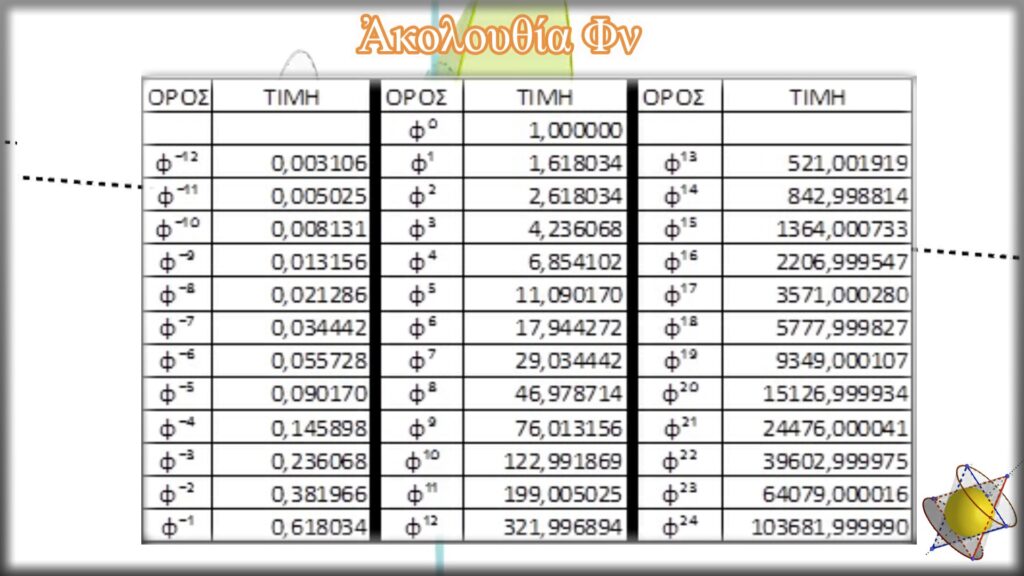
Μοναδικὴ ἰδιότητα τῆς ἀκολουθίας Φν εἶναι ὅτι ὁ κάθε ἑπόμενος ὄρος της εἶναι ἴσος μὲ τὸ ἄθροισμα τῶν δύο προηγούμενων ὅρων.
Φν+1=Φν+Φν-1
Παρατηροῦμε ὅτι, ὅσο ἡ ἀκολουθία ἐξελίσσεται, τόσο ἡ ἀριθμητικὴ της τιμὴ τείνει νὰ γίνει ἀκέραιος ἀριθμός, χωρὶς ὅμως αὐτὸ νὰ ἐπιτυγχάνεται. Ἡ προσέγγιση αὐτὴ γίνεται ἐναλλάξ, τὴν μία φορὰ μὲ τιμὴ μικρότερη ἀπὸ τὴν ἀκέραια τιμὴ καὶ τὴν ἄλλη μὲ τιμὴ μεγαλύτερη.
Μάλιστα, ὅσο ἡ τιμὴ τοῦ ἀριθμοῦ ν τείνει στὸ ἄπειρο, τόσο καὶ ἡ προσέγγιση αὐτὴ μεγαλώνει μὲ ἕνα πολὺ συγκεκριμένο τρόπο. Ἡ ἀπόκλιση τῆς τιμῆς τοῦ κάθε ὅρου τῆς ἀκολουθίας ἀπὸ τὸν πλησιέστερο ἀκέραιο ἀριθμὸ εἶναι συγκεκριμένη καὶ ἰσοῦται μὲ τὴν τιμὴ τοῦ ἀντίστοιχου ὅρου φ-ν
│φν -Ζ(φν)│=φ-ν
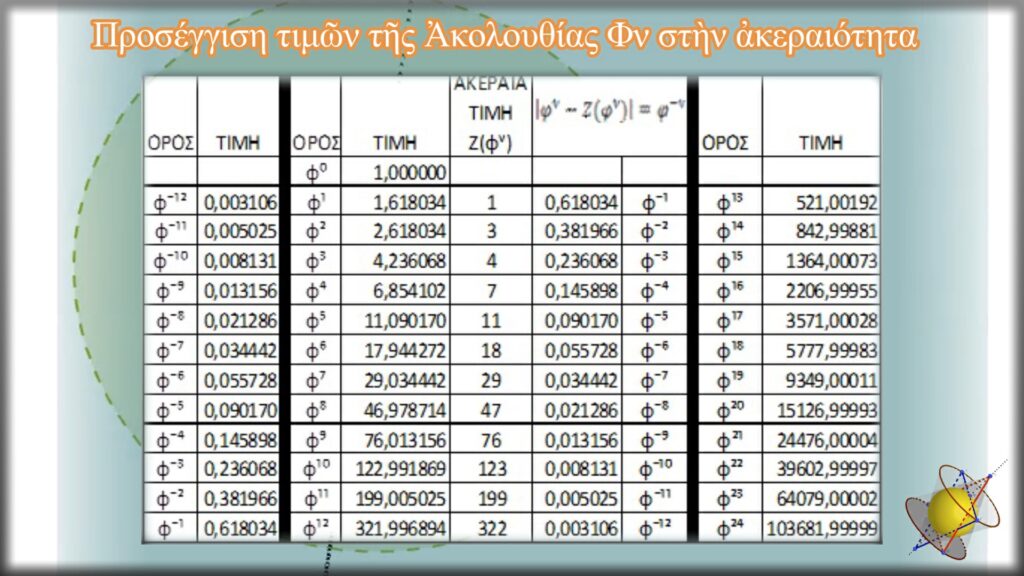
Μιὰ ἐπίσης πολὺ σημαντικὴ ἰδιότητα τῆς ἀκολουθίας Φν καὶ γιὰ πρῶτο ὅρο τὸν Φ0=φ0=1, μᾶς ὑποδεικνύει ὅτι ὁ κάθε ἑπόμενος ὄρος της εἶναι ἴσος μὲ τὸ ἄθροισμα ὅλων τῶν προηγούμενων ὅρων της, σὺν τὴν τιμὴ φ.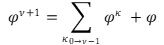
Τὴν ἰδιότητα αὐτή, ὅπως καὶ τὴν απόδειξή της, τὴν εἴδαμε στὸ βιβλίο «Γεωμετρικὲς Κατασκευὲς στὸ Πὶ καὶ Φί».
Ἂν λοιπὸν θεωρήσουμε ὅτι ἡ ἀκολουθία Φν, ἢ ἀνάλογες μὲ αὐτὴν τὴν μορφὴ ἀκολουθίες, μποροῦν νὰ περιγράψουν φυσικὰ ἐξελικτικὰ φαινόμενα, τότε φαίνεται ὅτι τὸ ἀποτέλεσμα τοῦ μεγέθους ποὺ ἡ ἀκολουθία περιγράφει, μετὰ ἀπὸ κάθε ἑπόμενο βῆμα αὐτῆς τῆς ἐξελικτικῆς πορείας, περιλαμβάνει ὅλα τὰ προηγούμενα ποσὰ σὺν μιὰ σταθερή, ἀπαραίτητη καὶ κβαντισμένη τιμή, τὴν τιμὴ φ.
Ἐπίσης, ἀποδεικνύεται ὅτι τὸ ἄθροισμα ὅλων τῶν ἀρνητικῶν ὅρων τῆς ἀκολουθίας εἶναι ἴσο μὲ φ
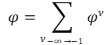
Μποροῦμε λοιπὸν νὰ συμπεράνουμε ὅτι ὁ κάθε ἑπόμενος ὅρος τῆς ἀκολουθίας Φν εἶναι ἴσος μὲ τὸ ἄθροισμα ὅλων τῶν προηγούμενων του.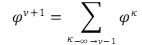
Μετατροπὴ τῶν ὅρων τῆς ἀκολουθίας Φν σὲ διώνυμα
Κάθε ὅρος τῆς ἀκολουθίας μπορεῖ νὰ χαρακτηριστεῖ καὶ σὰν μονώνυμο ν-οστού βαθμοῦ, δηλαδὴ βαθμοῦ ἴσου μὲ τὴ δύναμη στὴν ὁποία εἶναι ὑψωμένος. Στὴ συγκεκριμένη ὅμως ἀκολουθία ἰσχύει ἡ μοναδικὴ ἰδιότητα, ὁπου ὁ κάθε ὅρος της εἶναι ἴσος μὲ τὸ ἄθροισμα τῶν δύο προηγούμενων. Ἔτσι, μᾶς δίνεται ἡ δυνατότητα νὰ μετατρέψουμε ὅλους τοὺς ὅρους, (ἀπὸ τὸν φ² καὶ μετά), σὲ διώνυμα πρώτου βαθμοῦ, ὅπως φαίνεται στὸν ἑπόμενο πίνακα.
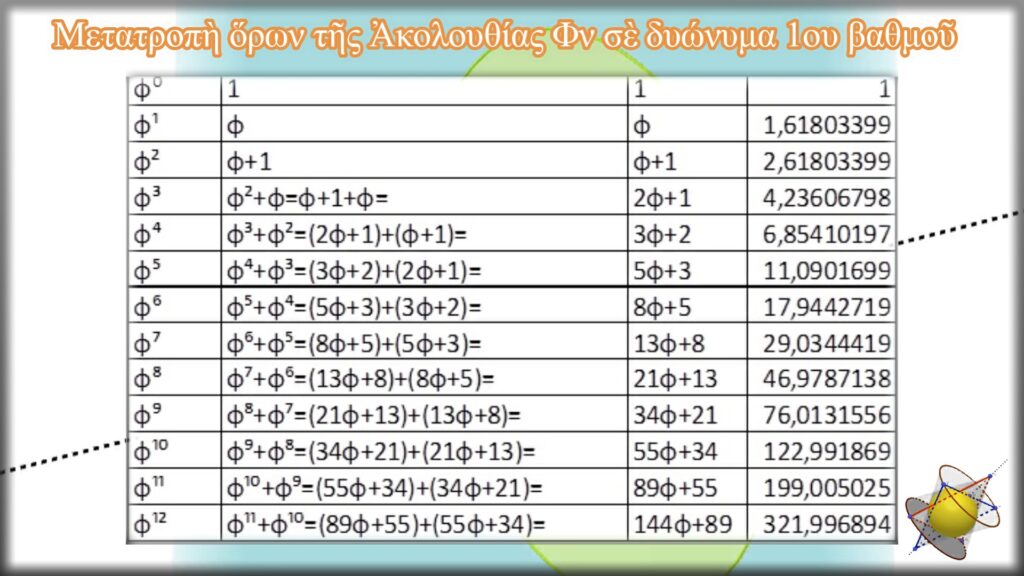
Πώς μπορεῖ ὅμως ἡ ἀκολουθία Φν νὰ κάνει πράξη τὴν ἐπιθυμία τῶν ὅρων της νὰ πάρουν ἀκέραιες τιμές;

