Ὁ τετραγωνισμὸς τοῦ κύκλου στὸ Πὶ καὶ Φί
Ὁ ἐνδιάμεσος ἀριθμὸς δ καὶ ἡ ἀκολουθία του
Ἀπό τὸ βιβλίο…

Ὁ ἐνδιάμεσος ἀριθμὸς δ
Ἂς θυμηθοῦμε πάλι τὸ Χρυσὸ Τρίγωνο, ὅπου ΑΜ=ΒΓ=φ. Ἐπειδὴ τὸ τρίγωνο εἶναι καὶ ἰσοσκελές, ἔχουμε ὅτι: ΒΜ=φ/2 καὶ ΑΒ=√5·φ/2.
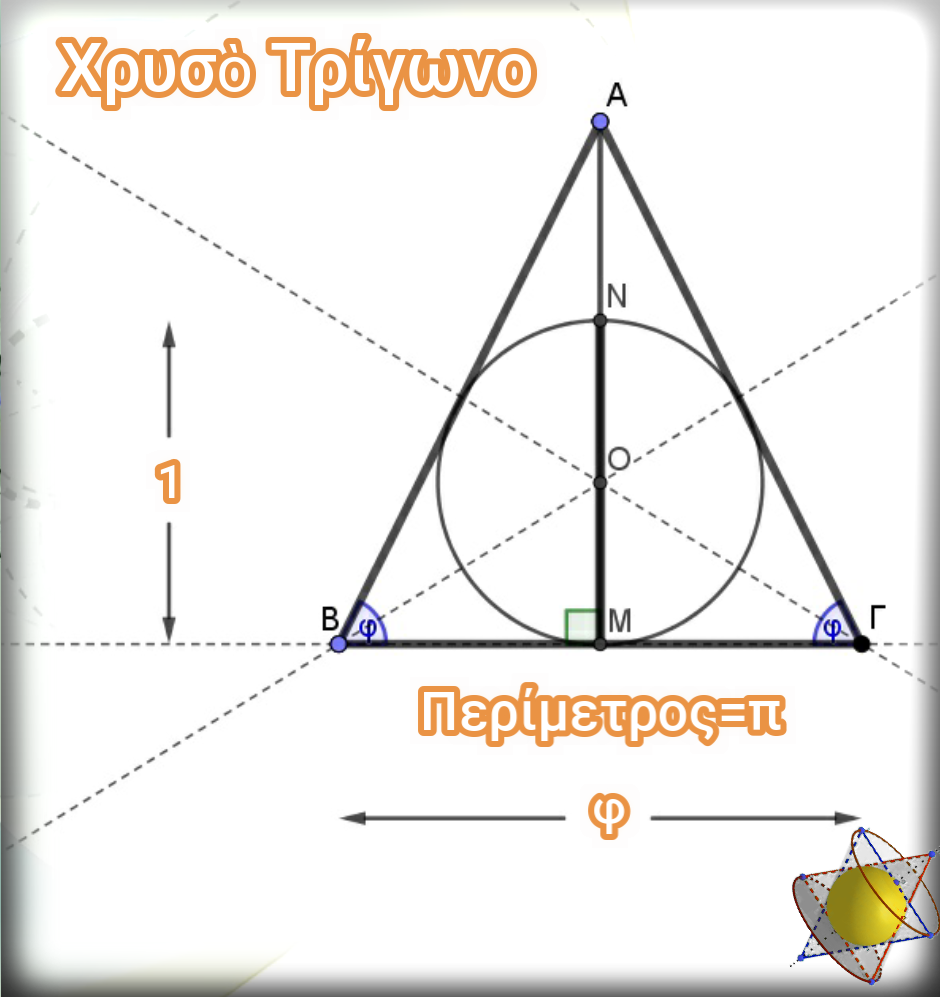
Ὑπολογίζουμε τὸ ημω καὶ τὸ συνω τῆς γωνίας Β καὶ στὴ συνέχεια τὸ ἄθροισμα τους.
Αὐτὸ εἶναι:
Ποιό εἶναι ὅμως τὸ ἐντυπωσιακό; Εἶναι ἡ τιμὴ του.
Προκύπτει πὼς
Αὐτὸν τὸν ἀριθμό, γιὰ εὐκολία θὰ τὸν ὀνομάσουμε ἐνδιάμεσο ἀριθμὸ δ, ποὺ ὅπως εἴδαμε ἀπὸ τὸ Χρυσὸ τρίγωνο, ἔχει ἄμεση σχέση τόσο μὲ τὸν μοναδιαίο κύκλο, ὅσο καὶ μὲ τὴν τιμὴ τοῦ ἀριθμοῦ πφ ποὺ προκύπτει ἀπὸ αὐτὸν.
Παρατηροῦμε ἐπίσης, ὅτι ὁ Μοναδιαῖος Κύκλος ὁριοθετεῖται ἐπακριβῶς ἀνάμεσα στὶς δύο γωνίες τῆς βάσης τοῦ Χρυσοῦ Τριγώνου. Εἶναι γωνίες ποὺ καθορίζουν τὶς τριγωνομετρικὲς τιμὲς τοῦ ἡμίτονου καὶ τοῦ συνημίτονου καὶ κατ’ ἐπέκταση τὴν τιμὴ τοῦ ἀριθμοῦ δ. Ἔτσι, θὰ μπορούσαμε νὰ ποῦμε στὴν πράξη ὅτι ὁ ἐνδιάμεσος ἀριθμὸς δ ἐπιδρᾶ στὴν ημι-περίμετρο τοῦ Μοναδιαίου Κύκλου.
Τύπος τῆς ἐνδιάμεσης τιμῆς
Ὑπάρχει ἀκόμη μιὰ σχέση, ἕνας τύπος, ποὺ πηγάζει ἀπὸ τὸν ἀριθμὸ δ.
ἄρα:
Αὐτὸς ὁ ἀριθμὸς δ εἶναι ὁ ἐνδιάμεσος, συνδετικὸς κρίκος τῶν ἀριθμῶν π καὶ φ, ὅπως θὰ δοῦμε στὴ συνέχεια.
Ἡ ἀκολουθία Δ
Ἂς ἀντιμετωπίσουμε τὸ Χρυσὸ Τρίγωνο, μαζὶ μὲ τὸν ἀντίστοιχο ἐγγεγραμμένο σὲ αὐτὸ Κύκλο, σὰν ἕνα συμπαντικὸ φυσικὸ ἐξελικτικὸ φαινόμενο ποὺ μπορεῖ νὰ περιγραφεῖ ἀπὸ μία ἀκολουθία τῆς μορφῆς Δν=δ·φν. Αὐτὴ θὰ παίρνει τιμὲς γιὰ ἀκέραιες τιμὲς τοῦ ν, ἀπὸ τὸ -∞ ἕως τὸ +∞. Ἡ σταθερὰ δ εἶναι ὁ ἐνδιάμεσος ἀριθμὸς Ὁ κάθε ὅρος θὰ ἀντιστοιχεῖ σὲ Χρυσὸ Τρίγωνο ΑΒΓ μὲ βάση ΒΓ=φν+1 καὶ σὲ ἀντίστοιχο Κύκλο (Κ,ρ) μὲ διάμετρο 2ρ ἴση μὲ τὴν τιμὴ φν .Ἔτσι, ὁ ὅρος Δ0=δ θὰ ἀντιστοιχεῖ στὸ Χρυσὸ Τρίγωνο μὲ βάση ΒΓ=φ καὶ στὸν ἀντίστοιχο, ἐγγεγραμμένο μοναδιαίο Κύκλο (Κ,0,5) διότι ἡ διάμετρος θὰ εἶναι ἴση μὲ τὴν μονάδα.
Μὲ βάση τὰ παραπάνω συμπληρώνουμε τὸν ἑπόμενο πίνακα.
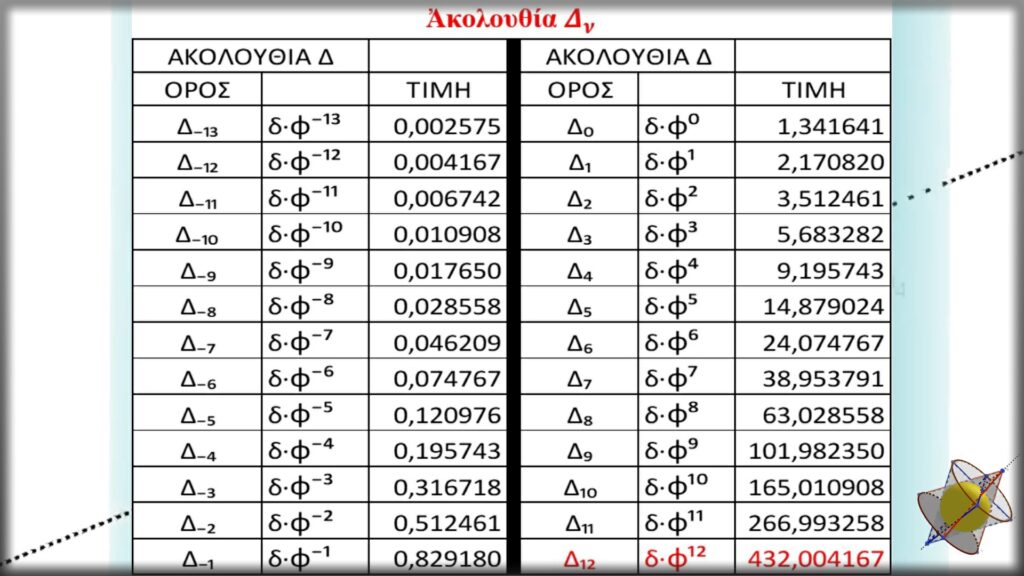
Εἶναι ἐμφανὲς καὶ ἀναμενόμενο πὼς καὶ ἡ ἀκολουθία Δ ἀκολουθεῖ τοὺς γενικώτερους κανόνες τῆς ἀκολουθίας Φ. Μεγάλο ἐνδιαφέρον ἔχει ἡ τιμὴ τοῦ 12ου ὅρου. Μάλιστα ἂν ἀπὸ αὐτὴν ἀφαιρέσουμε τὴν τιμὴ τοῦ ὅρου Δ-12 , (ὅπως συμβαίνει καὶ μὲ τὴν ἀκολουθία Φ), τότε παίρνει τὴν ἀκέραια τιμὴ 432.
Εἶναι ἡ πρώτη ἐμφάνιση τοῦ σημαντικοῦ αὐτοῦ ἀριθμοῦ ποὺ προκύπτει μὲ μαθηματικὴ λογικὴ ἀκολουθία σκέψης. Θὰ ἀκολουθήσουν καὶ ἄλλες.
Ἡ τιμὴ 432 εἶναι ἡ τιμὴ ποὺ ἀρχικὰ δόθηκε γιὰ νὰ ὁρίσει τὴν συχνότητα ἀναφορᾶς κουρδίσματος γιὰ τὴν νότα Λα. Ἡ νότα Λα θεωρεῖται ἡ πρώτη νότα σὲ ἕναν πλήρη μουσικὸ κύκλο καὶ ἡ ὁποία ἐμφανίζεται ξανὰ μετὰ ἀπὸ 12 ἐξελικτικὰ βήματα. Γι’ αὐτὸ καὶ συμβολίζεται μὲ τὸ κεφαλαῖο λατινικὸ γράμμα Α. Μετὰ ὅμως ἀπὸ 12 ἐξελικτικὰ βήματα προέκυψε ἡ τιμὴ 432 καὶ στὴν ἀκολουθία Δ, ὑποδηλώνοντας τὴ σχέση τῆς μουσικῆς μὲ τὸν συγκεκριμένο ἀριθμὸ καὶ ἑπομένως καὶ μὲ τὸ χρυσὸ τρίγωνο. Ἐκτενὴς ἀναφορὰ θὰ γίνει στὴν παρουσίαση τῆς Τετρακτύος.
Ἔχουμε λοιπὸν τὴν τιμὴ τοῦ 12ου ὅρου τῆς ἀκολουθίας Δ ποὺ προέκυψε σὰν φυσικὸ ἐξελικτικὸ φαινόμενο ὅπου, ὅπως συμβαίνει μὲ ὅλα τὰ ἐξελικτικὰ φαινόμενα, ἐμπλέκεται ὁ ΧΡΟΝΟΣ. Ἔχουμε ὅμως καὶ τὴν ἀκέραια τιμὴ 432 ποὺ προέκυψε μὲ μιὰ ἁπλὴ μαθηματικὴ πράξη ἀφαίρεσης (Δ12-Δ-12=432), δηλαδὴ πράξης ὅπου δὲν ὑπεισέρχεται ἡ ἔννοια τοῦ χρόνου. Εἴδαμε ἐπίσης ὅτι ὁ ἐνδιάμεσος ἀριθμὸς δ μᾶς ἔδωσε τὴν τιμὴ τοῦ ἀριθμοῦ πφ. Ἀντίστοιχα ἡ ἰσχύουσα τιμὴ π προκύπτει μέσα ἀπὸ μαθηματικὲς προσεγγίσεις ὅπου καὶ πάλι δὲν ὑπάρχει ἡ ἐμπλοκὴ τοῦ χρόνου.
Ἡ τιμὴ τοῦ π ἐντὸς μετρήσιμων ὁρίων
Ἐὰν θὰ θέλαμε νὰ μετρήσουμε μὲ ἀκρίβεια τὸ πλῆθος ἑνὸς μεγάλου σμήνους πουλιῶν τὴν ὥρα ποὺ πετοῦν, αὐτὸ θὰ ἦταν ἀδύνατον. Ὁ μόνος τρόπος θὰ ἦταν νὰ παγώσουμε τὸν χρόνο, γιὰ παράδειγμα μὲ μιὰ φωτογραφία. Στὸ Σύμπαν ὅμως, σὲ φυσικὴ ροὴ αὐτὸ δὲν μπορεῖ νὰ συμβῆ, ὁ χρόνος δὲν μπορεῖ νὰ παγώσει.
Θὰ ἐπιχειρήσουμε μία μεγάλη ὑπέρβαση.
Θὰ προσπαθήσουμε νὰ ἐπιβραδύνουμε ὅσο μποροῦμε τὸν χρόνο, μὲ ἀπώτερο στόχο τὴ βελτίωση τῆς τιμῆς δ, ὥστε, μὲ χρήση τοῦ τύπου τῆς ἐνδιάμεσης τιμῆς δ+δ2=δ(δ+1)=πφ νὰ προκύψει ἡ τιμὴ τοῦ ἀριθμοῦ π, ὅπως μᾶς εἶναι γνωστὴ στὸν περιορισμένο τρισδιάστατο (εὐκλείδειο) χῶρο.
Θὰ προσπαθήσουμε νὰ ἐφαρμόσουμε ὅποια συμπεράσματα προέκυψαν ἀπὸ τὴν ἀκολουθία Φ, καθὼς καὶ ἀπὸ τὶς τρεῖς σειρές, Fibonacci, Lucas καὶ Χ. Θὰ ἑστιάσουμε τὴν προσοχὴ μας σὲ τέσσερεις βασικὲς κατευθύνσεις ποὺ μᾶς ὑποδείχθηκαν. Αὐτὲς εἶναι:
1η Ἡ ὁλοκλήρωση ἑνὸς κύκλου τοῦ φαινομένου σὲ δώδεκα βήματα.
2η Ἡ τάση καὶ «ἐπιθυμία» τῶν ὅρων της νὰ συγκλίνουν σὲ ἀκέραιες τιμές, κινούμενη μὲ συγκεκριμένους περιορισμούς.
3η Ἡ ὕπαρξη μικρότερου ὅρου (Δ-12) μὲ ὑπολογιστικὴ ἀξία, ὅταν αὐτὸ ἐπιθυμοῦμε.
4η Ἡ ἀπόκλιση τοῦ ὅρου αὐτοῦ ἀπὸ τὴ τιμὴ ποὺ μᾶς ὑποδείχθηκε.
…
Ἡ βελτιωμένη κατὰ τὴν ἐπιθυμία μας τιμὴ τοῦ ἀριθμοῦ δ, ὅπως ἀναλυτικὰ περιγράφεται στὸ βιβλίο μου ¨ Ἡ Χρυσὴ Τομὴ στὴ Μουσική¨ εἶναι :
δτ= 1,3416277185545, ἡ ὁποία δίνει γιὰ τὸν ἀριθμὸ π τὴν τιμὴ:
δτ+δτ2=3,1415926537483=π
Ἡ ἰσχύουσα τιμὴ τοῦ ἀριθμοῦ π εἶναι 3,1415926535898
Ἡ ἀπόκλιση α εἶναι τῆς τάξης τοῦ 10-11, α=0000000000504
Εἶναι πολὺ σημαντικὸ καὶ ἐπιθυμητὸ τὸ ὅτι ἡ τιμὴ ποὺ βρέθηκε εἶναι κατὰ ἐλάχιστα μεγαλύτερη καὶ ὄχι ἴση ἢ μικρότερη ἀπὸ τὴν ἰσχύουσα.
Ὁ λόγος εἶναι ὅτι γιὰ κάθε ἀπόκλιση ποὺ βρέθηκε καὶ ἀφαιρέθηκε, ὑπάρχει καὶ ἡ δικὴ της ἀπόκλιση, ἡ ὁποία ὅμως δὲν ὑπολογίστηκε γιὰ νὰ ἀφαιρεθεῖ.
Στὴν πράξη ὁ λόγος εἶναι ὅτι ἐπιβραδύναμε τὸν χρόνο ὅσο μπορούσαμε χωρὶς ὅμως νὰ τὸν σταματήσουμε.
Εἶναι ἕνας ἐπαναλαμβανόμενος κύκλος ποὺ συμβαδίζει ἀπόλυτα μὲ τὴν ὑπερβατικώτητα τῆς ἰσχύουσας τιμῆς τοῦ ἀριθμοῦ π.
Αὐτὴ εἶναι λοιπὸν ἡ πρόταση τοῦ ἀριθμοῦ φ γιὰ τὴν τελικὴ τιμὴ τοῦ ἀριθμοῦ π, ἡ ὁποία θὰ μποροῦσε καὶ περαιτέρω νὰ βελτιωθεῖ.
Συμπεράσματα
Βλέπουμε λοιπὸν ὅτι ὁ ἀριθμὸς φ καὶ ἡ ἀκολουθία του μᾶς ἔδωσαν στὴν οὐσία δύο τιμὲς γιὰ τὸν ἀριθμὸ π. Ἡ πρώτη τιμὴ εἶναι ἡ πφ=6/5·φ² ποὺ τὴν ἑρμηνεύσαμε καὶ σὰν τὴν τιμὴ ποὺ προκύπτει ὅταν ἀντιμετωπίσουμε τὸ πρόβλημα σὰν φαινόμενο ποὺ ἐξελίσσεται ὁμαλὰ καὶ χωρὶς περιορισμοὺς στὸ ἄπειρο. Ἡ δεύτερη τιμὴ προκύπτει ὅταν τὸ προηγούμενο ἐξελικτικὸ φαινόμενο τὸ θέσουμε ἐντὸς ὁρίων. Μάλιστα, ἡ τιμὴ αὐτὴ σχεδὸν ταυτίζεται μὲ τὴν σημερινὰ ἀποδεκτὴ καὶ ἀποδεδειγμένη τιμὴ τοῦ π.
Ποιὰ ἀπὸ τὶς δύο τιμὲς εἶναι ὅμως ἡ σωστή;
Σωστὲς εἶναι καὶ οἱ δύο.
Ἂς ἀφήσουμε τὴν φαντασία μας ἐλεύθερη καὶ μὲ ἕνα παράδειγμα, ἂς προσπαθήσουμε νὰ τεκμηριώσουμε τὴν παραπάνω ἀπάντηση.

