Ὁ τετραγωνισμὸς τοῦ κύκλου στὸ Πὶ καὶ Φί
Εὔρεση τοῦ ἀριθμοῦ π μὲ τὴ χρήση τοῦ κύκλου
Ἀπὸ τὸ βιβλίο…

Ὁ πρωτότυπος γεωμετρικὸς μηχανισμός, ποὺ πιὸ πρὶν εἴδαμε, μὲ τὸν τρόπο του, ἔστω καὶ προσεγγιστικά, μᾶς ἔδωσε τὸν ἀριθμὸ π, μᾶς ἔδωσε καὶ τὸν τετραγωνισμὸ τοῦ κύκλου, χωρὶς ὅμως νὰ τὸν χρησιμοποιεῖ στὴν κατασκευή. Σίγουρα, ἡ ἴδια ἡ ἐμπλοκὴ τοῦ κύκλου στὴν κατασκευὴ γιὰ τὴν εὕρεση τοῦ ἀριθμοῦ π, θὰ ἐνίσχυε κατὰ πολὺ τὴν πεποίθηση μας περὶ ὀρθότητας τοῦ ἐγχειρήματος μας, θὰ ἐνίσχυε καὶ τὶς προσδοκίες μας. Ὑπάρχει ὅμως αὐτὴ ἡ δυνατότητα;
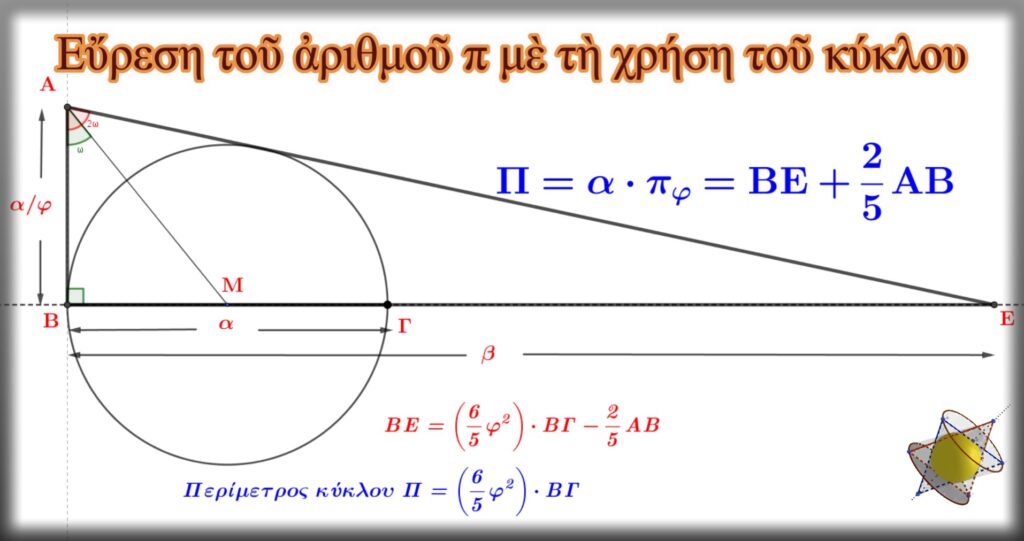
Κατασκευή
Ἔστω ὅτι ἔχουμε κύκλο μὲ διάμετρο ΒΓ=α.
Ἀφοῦ φέρουμε τὴν κάθετη στὴν ΒΓ εὐθεία ἀπὸ τὸ σημεῖο Β, πάνω σὲ αὐτὴν παίρνουμε εὐθύγραμμο τμῆμα ΑΒ=α/φ. Αὐτὸ εὔκολα κατασκευάζεται γιατὶ εἶναι ἴσο μὲ τὸ μεγαλύτερο ἀπὸ τὰ δύο εὐθύγραμμα τμήματα ποὺ ἡ χρυσὴ τομὴ τοῦ ΒΓ εὐθύγραμμου τμήματος δημιουργεῖ.
Ἀπὸ τὸ σημεῖο Α φέρνουμε τὴν ἐφαπτόμενη στὸν κύκλο, ἡ ὁποία τέμνει τὴν προέκταση τῆς διαμέτρου ΒΓ στὸ σημεῖο Ε.
Ἀποδεικνύεται (ἐδῶ), πὼς ΒΕ=ΒΓ·(6/5·φ²)-2/5·ΑΒ καὶ ἐὰν θεωρήσουμε ὅτι 6/5·φ²= πφ =π, τότε ΒΓ·(6/5·φ²) εἶναι ἴσο μὲ τὴν περίμετρο τοῦ συγκεκριμένου κύκλου Π, ὁπότε :
Π=ΒΕ+2/5·ΑΒ τὸ ὁποῖο εὔκολα κατασκευάζεται.
Φυσικά, ἐὰν ἡ διάμετρος τοῦ κύκλου θὰ ἰσοῦται μὲ τὴν μονάδα (δ=1), τότε ἡ περίμετρος Π θὰ ἰσοῦται μὲ τὸν ἀριθμὸ π. (Π=δ·π)
Ἡ κατασκευὴ φαίνεται πὼς εἶναι ἰδιαίτερα σημαντικὴ διότι οἱ ἀπολύτως συγκεκριμένες διαστάσεις τοῦ κύκλου εἶναι αὐτὲς ποὺ μᾶς ὁδήγησαν στὸ ἴδιο ἀποτέλεσμα. Εἶναι ἕνα ἀποτέλεσμα ποὺ μᾶς χαροποιεῖ, ἀλλὰ μᾶς προβληματίζει ἀκόμη περισσότερο. Γιατὶ νὰ συμβαίνει; Γιατὶ νὰ μᾶς ὑποδεικνύεται τόσο ἐμφατικὰ καὶ μὲ διάφορους τρόπους μιὰ διαφορετικὴ τιμὴ γιὰ τὸν ἀριθμὸ π; Γιατὶ σύσσωμη ἡ ἐπιστημονικὴ κοινότητα θέλησε ἑρμητικὰ νὰ κλείσει τὸ θέμα, ἀρνούμενη πεισματικὰ ἀκόμη καὶ νὰ ἐλέγξει τὰ ὅποια νέα στοιχεῖα;
Ἡ ἀπάντηση στὸ τελευταῖο «γιατὶ» ἴσως νὰ βρίσκεται στὴ διαφορετικὴ μορφὴ ἐγωισμοῦ ἀντιμετώπισης μίας ἀποτυχίας, ποὺ κάποιοι τὴν ξεπερνοῦν μὲ τὴ φράση «Δὲν γίνεται» καὶ κάποιοι ἄλλοι τὴν ἀποδέχονται μὲ τὴ φράση « Δὲν μπόρεσα…». Ἴσως πάλι νὰ βρίσκεται στὴ δεδομένη διαβάθμιση γνώσεων ποὺ ὑπάρχει ἀπὸ τὰ χρόνια τῶν Πυθαγόρειων μέχρι καὶ στὶς μέρες μας, ὅπως φαίνεται και με τὴν (μὴ) δυνατότητα πρόσβασης στὴν βιβλιοθήκη τοῦ Βατικανοῦ καὶ ἡ ὁποία μᾶς ἐπιτρέπει νὰ ὑποθέσουμε τὰ πάντα.
Τὸ πρόβλημα ὅμως τέθηκε δημόσια γι’ αὐτὸ εἴμαστε ὑποχρεωμένοι νὰ συνεχίσουμε ἀφήνοντας τὰ νέα δεδομένα νὰ μᾶς ὁδηγήσουν σ’ ένα συναρπαστικὸ ταξίδι ποὺ μόλις ξεκίνησε.

