Ὁ τετραγωνισμὸς τοῦ κύκλου στὸ Πὶ καὶ Φί
Σειρὰ Fibonacci
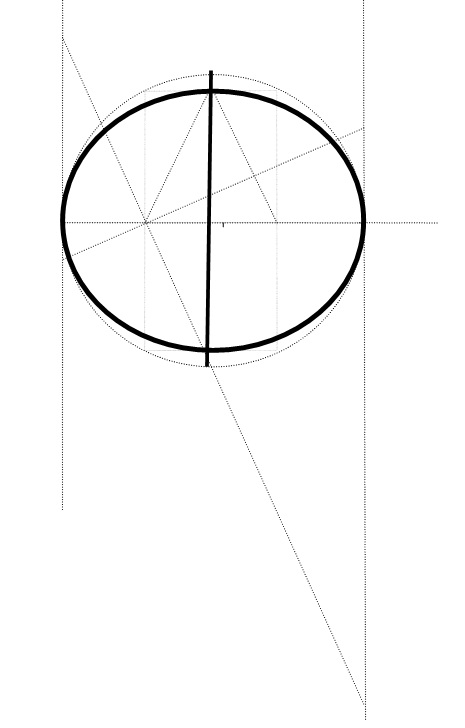
Ἀπό τὸ βιβλίο…

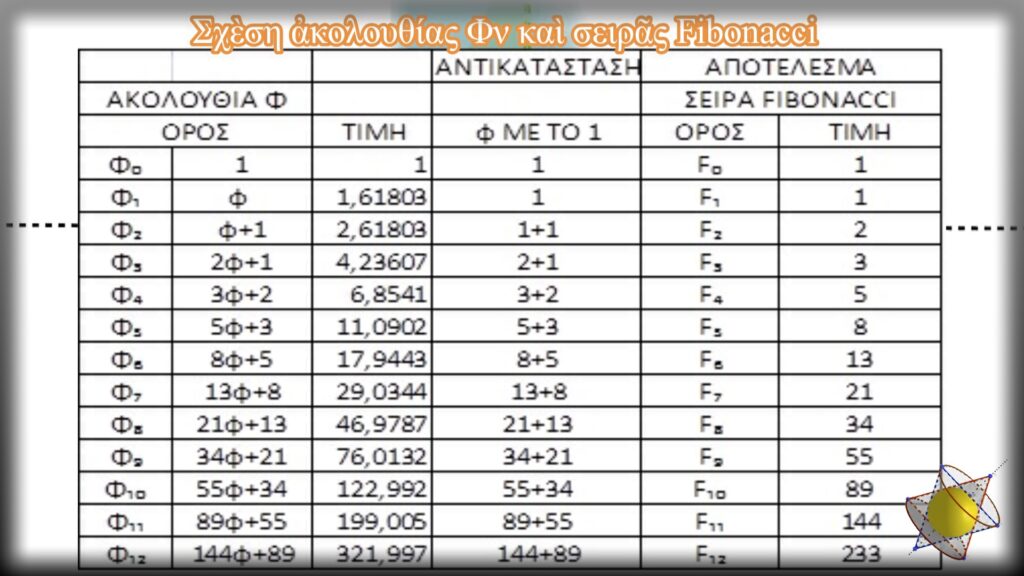
Σχέση ἀκολουθίας Φν καὶ σειρᾶς Fibonacci
Ὁ Fibonacci ὅρισε μία σειρὰ ἀκεραίων ἀριθμῶν μὲ πολὺ ἰδιαίτερα χαρακτηριστικά. Ὅρισε σὰν πρῶτο ὅρο τὴ μονάδα καὶ σὰν δεύτερο ὅρο ἐπίσης τὴ μονάδα. Ὁ κάθε ἑπόμενος ὅρος προκύπτει ἀπὸ τὸ ἄθροισμα τῶν δύο προηγούμενων. Ἔτσι, δημιουργήθηκε ἡ παρακάτω σειρὰ ἀκεραίων θετικῶν ἀριθμῶν: 1,1,2,3,5,8,13,21,34,55,89,144,…
Χαρακτηριστικὴ ἰδιότητα της εἶναι ὅτι τὸ πηλίκο δύο διαδοχικῶν ὅρων της (μεγαλύτερου πρὸς μικρότερο), τείνει πρὸς τὸν ἀριθμὸ φ, ὅσο ἡ σειρὰ ἐξελίσσεται. Παρατηρήσεις σὲ ἐξελικτικὰ φυσικὰ φαινόμενα, ὅπως καὶ σὲ ἀνθρώπινες κατασκευές, ἔδειξαν ὅτι βασίζονται στὴν συγκεκριμένη σειρά, ὅταν αὐτὰ πρέπει νὰ ἐκφραστοῦν μὲ ἀκέραιες τιμές. Πολλὲς προσπάθειες ἔγιναν γιὰ νὰ βρεθεῖ πὼς προκύπτει ἡ σχέση ποὺ ὑπάρχει μεταξὺ τῆς σειρᾶς Fibonacci καὶ τῆς ἀκολουθίας φ. Παρακάτω, θὰ ἀποκαλυφθεῖ αὐτὴ ἡ σχέση.
Ἐργαζόμενοι στὸν πίνακα ποὺ ἀποδίδει τοὺς ὅρους τῆς ἀκολουθίας μὲ μορφὴ διωνύμου (ἐδῶ), θὰ ἀντικαταστήσουμε στὰ διώνυμα τὴν τιμὴ τοῦ ἀριθμοῦ φ μὲ τὸν ἀμέσως μικρότερο ἀκέραιο, δηλαδὴ τὴν μονάδα καὶ θὰ κάνουμε τὴν πρόσθεση.
Ἔτσι ἁπλά, τὸ ἀποτέλεσμα εἶναι ἡ σειρὰ Fibonacci.
Γιὰ τοὺς ὅρους τῆς σειρᾶς Fibonacci ἰσχύει τύπος ἀνάλογος μὲ αὐτὸν τῆς ἀκολουθίας Φν.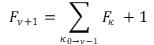
Εἶναι φανερὸ ὅτι γιὰ νὰ μεταβοῦμε στὸν κάθε ἑπόμενο ὅρο, ἡ τιμὴ ποὺ προστίθεται στὸ ἄθροισμα τῶν προηγούμενων ὅρων εἶναι ἡ στρογγυλοποιημένη πρὸς τὸν μικρότερο ἀκέραιο τιμὴ τῆς ἀπαραίτητης κβαντισμένης τιμῆς , δηλαδὴ ἡ μονάδα. Πρόκειται γιὰ μιὰ πολὺ σημαντικὴ παρατήρηση, ποὺ ἐνισχύει τὴν θεώρηση περὶ δυνατότητας ἐξήγησης ἐξελικτικῶν φαινομένων μὲ ἀκέραια περιγραφὴ ἀποτελεσμάτων, ἐφαρμόζοντας τὴν σειρὰ Fibonacci.
Ὁ λόγος τῶν τιμῶν τῶν ὅρων τῆς ἀκολουθίας Φν μὲ τῶν ἀντίστοιχων τῆς σειρᾶς Fibonacci τείνει σὲ συγκεκριμένη τιμὴ 1,382… Αὐτὴ ἡ τιμὴ δὲν εἶναι τυχαία. Εἶναι ἴση μὲ:
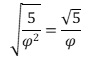
Τὴ σημασία τοῦ λόγου θὰ τὴν δοῦμε στὴν περιοδικότητα 12 βημάτων τῆς ἀκολουθίας Φν ποὺ θὰ ἀποκαλυφθεῖ ἀργότερα.
Εἶναι φανερὸ πὼς ἡ σειρὰ Fibonacci εἶναι μία ἁπλοποιημένη καὶ στρογγυλοποιημένη μορφὴ τῆς γεωμετρικῆς προόδου τοῦ ἀριθμοῦ φ. Ἐὰν λοιπὸν θὰ λέγαμε ὅτι ἡ ἀκολουθία ἀποτελεῖ θεμελιώδη συμπαντικὸ κανόνα περιγραφῆς ἁρμονικῆς λειτουργίας καὶ ἐξέλιξης φυσικῶν φαινομένων, τότε γιὰ τὰ μετρήσιμα μεγέθη, ποὺ θὰ θέλαμε ἢ θὰ ἐπιβάλλονταν νὰ ἔχουμε ἀκέραιες τιμὲς σὰν ἀποτέλεσμα, χρησιμοποιεῖται ἡ στρογγυλοποιημένη μορφὴ τῆς ἀκολουθίας φ ἀποκαλούμενη καὶ σὰν σειρὰ Fibonacci. Ἐπειδὴ μάλιστα ἡ στρογγυλοποίηση εἶναι πρὸς τὰ κάτω, τὸ ἀποτέλεσμα φυσικὰ εἶναι μικρότερο τοῦ ἀντίστοιχου ὅρου τῆς ἀκολουθίας Φν. Τὸ ὑπόλοιπο, λόγῳ τῆς στρογγυλοποίησης, δὲν χάνεται. Ἀντίθετα, αὐτὸ προστίθεται στὸ ἑπόμενο ἐξελικτικὸ βῆμα τῆς ἀκολουθίας ὁπότε καὶ μᾶς δίνεται νέο ὑπόλοιπο κ.ο.κ.
Παράδειγμα ἀποτελεῖ ἡ ἐξήγηση τοῦ δένδρου τοῦ Fibonacci.

