Ὁ τετραγωνισμὸς τοῦ κύκλου στὸ Πὶ καὶ Φί
Τὸ δένδρο του Fibonacci
Ἕνα ὑπέροχο παράδειγμα λειτουργίας τῆς Φύσης μέσα ἀπὸ ἀπολύτως προκαθορισμένα (κβαντισμένα) ἐνεργειακὰ πακέτα

Πρωτότυπη, πρώτη παρουσίαση…
Ἔχει παρατηρηθεῖ ὅτι σὲ πολλὲς περιπτώσεις ὁ ἀριθμὸς τῶν κλαδιῶν ἑνὸς δέντρου σὲ διαδοχικὰ ἐπίπεδα ανάπτυξής του, ἀκολουθεῖ τὴ σειρὰ Fibonacci. Ἡ παρατήρηση ὅμως εἶναι τὸ πρῶτο βῆμα. Γιατὶ καὶ μὲ ποιὸ τρόπο αὐτὸ συμβαίνει δὲν γνωρίζαμε. Τὶς ἀπαντήσεις καὶ τὰ ἀκόμη σημαντικώτερα συμπεράσματα θὰ δοῦμε στὴ συνέχεια.
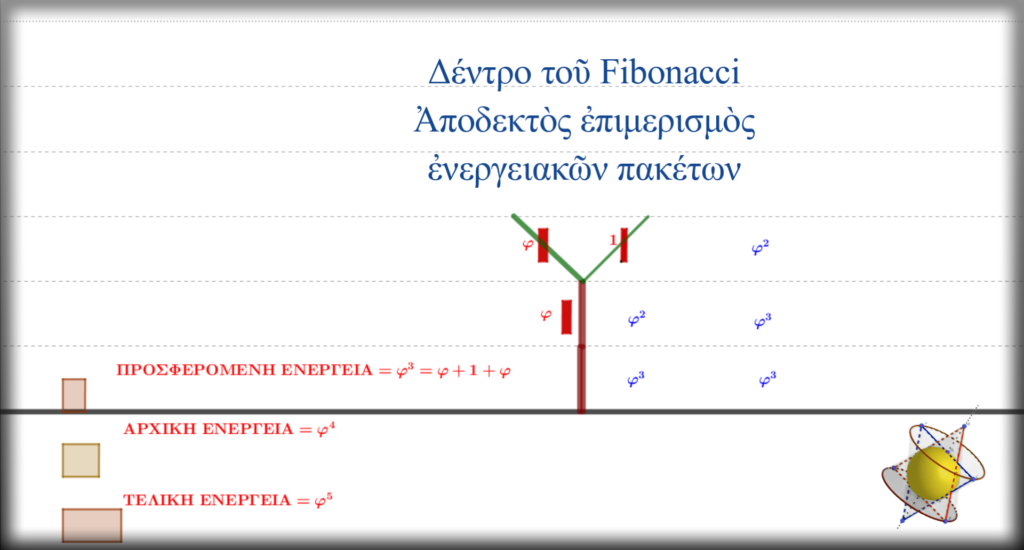
Θὰ δεχθοῦμε ὅτι ἡ ἀνάπτυξη ἑνὸς δέντρου εἶναι ἕνα φυσικὸ ἐξελικτικὸ φαινόμενο ὅπου σὲ κάθε ἑπόμενο ἐξελικτικὸ βῆμα του, ἡ συνολικὴ του ἐνέργεια γίνεται κατὰ φ φορὲς μεγαλύτερη. Αὐτὸ θὰ ἐπιτυγχάνεται κάθε φορὰ μὲ προσφερόμενη ἐνέργεια κατὰ φ φορές μικρότερη τῆς συνολικῆς ἐσωτερικῆς ἐνέργειας τοῦ δένδρου τῆς προηγούμενης φάσης ἀνάπτυξης. Ἡ ἐξήγηση βρίσκεται στὴν μοναδικὴ ἰδιότητα τῆς ἀκολουθίας Φ, ὅπου ὁ κάθε ἐπόμενος ὅρος της προκύπτει καὶ σὰν ἄθροισμα τῶν δύο προηγούμενων ὅρων. Ἔτσι, γιὰ παράδειγμα, ἐάν ἡ ὑπάρχουσα ἐσωτερικὴ ἐνἐργεια τοῦ δένδρου στην προηγούμενη φάση εἶναι φ², τότε ἡ προσφερόμενη ἐνέργεια στὴν ἐπόμενη φάση ἀνάπτυξης θὰ εἶναι ἴση με φ, οὗτος ὥστε ἡ συνολικὴ ἐνέργεια νὰ γίνει φ³ (φ²+φ=φ³).
Ἡ προσφερόμενη ἐνέργεια κάθε φορὰ εἶναι προκαθορισμένη καὶ διανέμεται σὲ κορμὸ καὶ κλαδιὰ μὲ ἀπολύτως καθορισμένα ἐπιμέρους ἐνεργειακὰ πακέτα.

Βασικὸς κανόνας εἶναι στὸ κάθε στάδιο ἀνάπτυξης νὰ προκύπτει συνολικὰ ὁλοκλήρωση τῆς φάσης τοῦ φαινομένου, χωρὶς δηλαδὴ ἐμφάνιση ἐλλείμματος ἢ πλεονάσματος στὴν ἀνάπτυξη τοῦ δέντρου.
Ὁ κορμὸς ἢ τὸ κάθε κλαδὶ τοῦ δέντρου ξεχωριστὰ μποροῦν νὰ ἀναπτυχθοῦν καθ’ ὕψος ἐφόσον εἶναι ἐλεύθερα ἀπὸ τὸ ἐπάνω μέρος τους.
Ἡ ἐλάχιστη προσφερόμενη ἐνέργεια γιὰ τὴν καθ’ ὕψος ἀνάπτυξη ἑνὸς κλαδιοῦ εἶναι ἡ θεμελιώδης, ἡ μοναδιαία ἐνέργεια.
Οἱ ἐσωτερικὲς ἐνέργειες μεταξὺ δύο διαδοχικῶν τμημάτων τοῦ δέντρου δὲν μποροῦν νὰ ἔχουν λόγο μεγαλύτερο τοῦ φ.
Κάθε ἑπόμενο κλαδὶ δὲν μπορεῖ νὰ ἔχει μεγαλύτερη ἐσωτερικὴ ἐνέργεια ἀπὸ τὸ προηγούμενο του.
Ἐὰν ἡ ἐσωτερικὴ ἐνέργεια ἑνὸς κλαδιοῦ εἶναι μεγαλύτερη τῆς μοναδιαίας ἀλλὰ ὄχι διπλάσια (μοναδικὴ ἱκανὴ καὶ ἀναγκαία συνθήκη εἶναι νὰ εἶναι ἴση μὲ φ=1,618…), καὶ ὑπάρχει προσφερόμενο ἐνεργειακὸ πακέτο ποὺ τηρεῖ τὶς παραπάνω προϋποθέσεις, τότε θὰ ἔχουμε καθ’ ὕψος ἀνάπτυξή του.
Τὸ κάθε ἐπιμέρους ἀνώτερο τμῆμα τοῦ κορμοῦ θὰ μπορεῖ νὰ διαχωριστεῖ δίνοντας δύο νέα κλαδιά, ἐφόσον ἡ ὑπάρχουσα ἐσωτερικὴ ἐνέργεια σὲ αύτὴν τὴν φάση, εἶναι τοὐλάχιστον διπλάσια τῆς θεμελιώδους, τῆς μοναδιαίας, καὶ ἐπειδὴ τὰ ἐνεργειακὰ πακέτα εἶναι συγκεκριμένα (κβαντισμένα), ἡ ἀμέσως μεγαλύτερη τοῦ 2 ἀποδεκτὴ ἐνεργειακὴ τιμὴ εἶναι ἡ τιμὴ φ²=2,618. Τὸν ἀριθμὸ 2 τὸν συναντοῦμε καὶ σὲ ἕνα ἄλλο σπουδαῖο φυσικὸ ἐξελικτικὸ φαινόμενο, τὸν πολλαπλασιασμὸ τῶν κυττάρων, ὅπου αὐτὰ διαχωρίζονται ὅταν διπλασιαστεῖ ὁ ἀριθμὸς τῶν χρωμοσωμάτων του. Στὴν περίπτωση τοῦ δέντρου, ἡ πλεονάζουσα τοῦ δύο ἐνέργεια φυσικὰ καὶ δὲν θὰ χάνεται, ἀντίθετα προσφέρεται σὲ ἕνα ἀπὸ δύο νέα κλαδιὰ αὐξάνοντας τὴν μάζα του καὶ ἑπομένως τὴν ἐνέργειά του.
Ἡ κατὰ ὕψος ἀνάπτυξη τοῦ δέντρου θὰ ἐπιτυγχάνεται ἐφόσον ἡ διατιθέμενη ἐνέργεια εἶναι ἐπαρκὴς γιὰ τὴν συνολικὴ ὁλοκλήρωση τοῦ συγκεκριμένου σταδίου.
Μὴ ἀποδεκτὲς ἐπιλογές
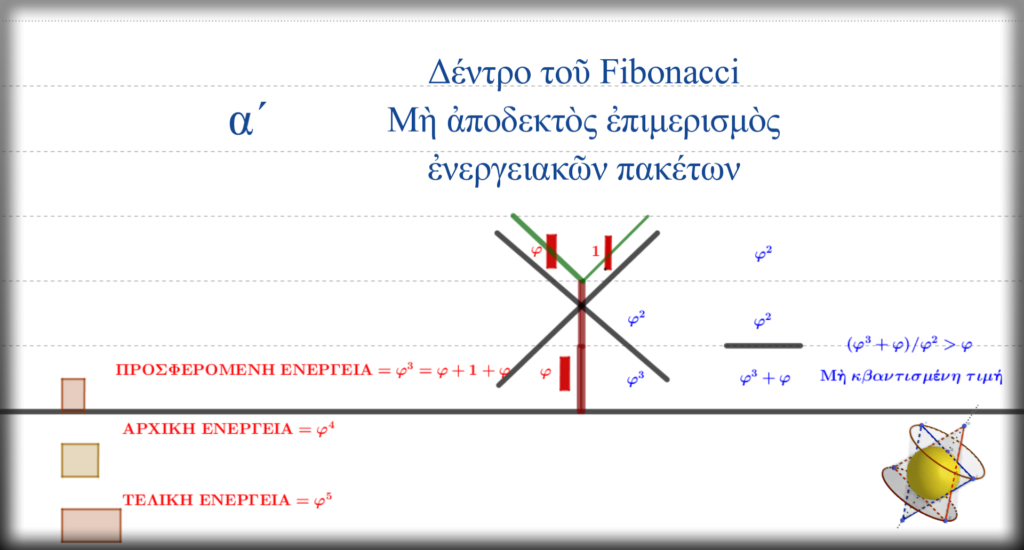

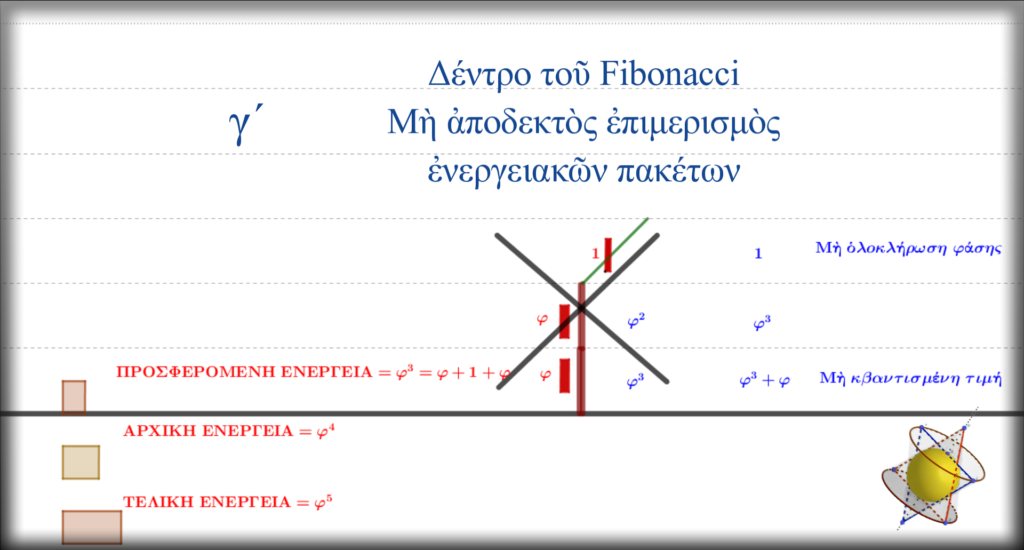
Ἂς πάρουμε τὴν ἐξέλιξη τοῦ φαινομένου ἀπὸ τὴν ἀρχή.
1ο βῆμα . Ἔχουμε τὴν ἐμφάνιση ἑνὸς μικροῦ κλαδιοῦ τοῦ ὁποίου ἡ ἐνέργεια ποὺ τοῦ δόθηκε γιὰ τὴν δημιουργία του ἔστω ὅτι εἶναι ἴση μὲ 1.
2ο βῆμα. Ἡ συνολικὴ ἐνέργεια αὐξάνεται κατὰ φ φορὲς καὶ γίνεται 1·φ=φ. Ἐπειδὴ ὅμως ἰσχύει: φ=1+1/φ, ἡ ἐπιπλέον ἐνέργεια εἶναι ἴση μὲ 1/φ. Αὐτὴ εἶναι ἀνεπαρκὴς γιὰ νὰ δώσει δεύτερο στάδιο καθ’ ὕψος ἀνάπτυξης (1/φ=0,618…<1), γιὰ αὐτὸ ὁ κορμὸς ἁπλῶς χοντραίνει ἔχοντας πλέον ἐνέργεια ἴση μὲ φ.
3ο βῆμα. Ἡ συνολικὴ ἐνέργεια τοῦ δέντρου γίνεται ἴση μὲ φ·φ=φ²=φ+1, δηλαδὴ ἡ ἐπιπλέον ἐνέργεια εἶναι ἴση μὲ 1. Αὐτὴ εἶναι ἱκανὴ νὰ μᾶς δώσει τὸ 2ο καθ’ ὕψος στάδιο ἀνάπτυξης τοῦ δέντρου.
4ο βῆμα. Ἡ συνολικὴ ἐνέργεια αὐξάνεται καὶ πάλι κατὰ φ φορὲς καὶ γίνεται ἴση μὲ φ·φ²=φ³=φ²+φ. Ἡ ἐπιπλέον ἐνέργεια εἶναι ἴση μὲ φ. Αὐτὴ ὅμως δὲν εἶναι ἀρκετὴ γιὰ νὰ δώσει ἐπιπλέον καθ’ ὕψος ἀνάπτυξη τοῦ δέντρου. Ἔτσι διαχωρίζεται σὲ δύο ἀπολύτως καθορισμένα ἐνεργειακὰ πακέτα 1 καὶ 1/φ, τὰ ὁποῖα μὲ τὴ ἴδια σειρὰ προστίθενται στὰ ὑπάρχοντα τμήματα τοῦ δέντρου αὐξάνοντας μάζα καὶ ὄγκο, τὰ ὁποῖα ἀποκτοῦν ἐπιμέρους ἐνέργειες ἴσες μὲ φ+1=φ² καὶ 1+1/φ=φ ἀντίστοιχα.
5ο βῆμα. Ἡ συνολικὴ ἐνέργεια γίνεται ἴση μὲ φ·φ³=φ⁴=φ³+φ², μὲ ἐπιπλέον ἐνέργεια ἴση μὲ φ². Καὶ πάλι τὸ ἐπιπλέον ἐνεργειακὸ πακέτο δὲν μπορεῖ νὰ προσφερθεῖ γιὰ καθ’ ὕψος ἀνάπτυξη τοῦ δέντρου γιατὶ ἂν καὶ εἶναι μεγαλύτερο τοῦ 2 ( =2,618…), τὸ προηγούμενο τμῆμα τοῦ κορμοῦ ἔχει ἐνέργεια μικρότερη (φ). Ἔτσι καὶ πάλι διαχωρίζεται σὲ δύο ἀπολύτως καθορισμένα ἐνεργειακὰ πακέτα, τὰ ὁποῖα μὲ τὴ ἴδια σειρὰ προστίθενται στὰ ὑπάρχοντα τμήματα τοῦ δέντρου μεγαλώνοντας τὶς διατομὲς τους καὶ τὶς ἐπιμέρους ἐνέργειες σὲ φ²+φ=φ³ καὶ φ+1=φ².
6ο βῆμα. Τώρα ἡ συνολικὴ ἐνέργεια εἶναι ἴση μὲ φ·φ⁴=φ⁵=φ⁴+φ³. Ἡ ἐπιπλέον ἐνέργεια φ³ διαχωρίζεται σὲ 2 ἐνεργειακὰ κβαντισμένα πακέτα φ καὶ φ² . Ἡ τιμὴ φ προστίθεται στὸ 2ο τμῆμα τοῦ κορμοῦ αὐξάνοντας τὴν ἐνέργειά του σὲ φ²+φ=φ³, καὶ τὸ πακέτο ἐνέργειας ἴσο μὲ φ² τηρεῖ ὅλες τὶς προϋποθέσεις γιὰ νὰ δώσει ἕνα νέο τμῆμα τοῦ κορμοῦ τοῦ δέντρου ἀποτελούμενο ἀπὸ δύο κλαδιά, ἕνα πιὸ χονδρὸ μὲ ἐνέργεια ἴση μὲ φ καὶ ἕνα λεπτότερο μὲ ἐνέργεια ἴση μὲ 1.
7ο βῆμα. Ἡ ἐνέργεια αὐξάνεται καὶ πάλι κατὰ φ φορὲς καὶ γίνεται ἴση μέ φ·φ⁵=φ⁶=φ⁵+φ⁴
Ἡ ἐπιπλέον ἀπολύτως καθορισμένη ἐνέργεια διαχωρίζεται σὲ δεδομένα κβαντισμένα ἐνεργειακὰ πακέτα, τὰ ὁποῖα προσφέρονται στὰ ἐπιμέρους τμήματα τοῦ κορμοῦ ἀπὸ κάτω πρὸς τὰ πάνω μὲ τὴν σειρὰ ποὺ φαίνεται στὴν ἑπόμενη ἰσότητα.
φ⁴=φ²+φ³=φ²+(φ²+φ)=φ²+(φ²+(1+1/φ))
Τὸ ἀποτέλεσμα εἶναι τὸ πάχος τῶν κορμῶν νὰ αὐξηθεῖ ἔχοντας πλέον ἐπιμέρους ἐνέργειες ἴσες μὲ φ³+φ²=φ⁴, φ³+φ²=φ⁴, ἐνῶ τὸ 3ο τμῆμα μὲ συνολικὴ ἐνέργεια ἴση μὲ φ³ ἀποτελεῖται πλέον ἀπὸ δύο κλάδους ἐνέργειας φ² καὶ φ ἀντίστοιχα.
8ο βῆμα. Ἡ συνολικὴ ἐνέργεια γίνεται φ·φ⁶=φ⁷= φ⁶+φ⁵
Ἡ ἐπιπλέον ἐνέργεια εἶναι ἴση μὲ φ⁵ ἡ ὁποία μοιράζεται σὲ καθορισμένα ἐνεργειακὰ πακέτα μὲ τὸν παρακάτω τρόπο.
φ⁵=φ³+φ⁴=φ³+(φ²+φ³)=φ³+(φ²+((φ+1)+φ))
Τὸ 1ο πακέτο ἐνέργειας προσφέρεται στὸ κατώτερο τμῆμα τοῦ κορμοῦ, αὐξάνοντας τὴν ενέργειά τοῦ σὲ φ⁴.
Τὸ 2ο ποσὸ φ², διαχωριζόμενο καὶ πάλι μὲ τὴν χρυσὴ ἀναλογία σὲ φ καὶ 1, προσφέρεται στοὺς 2 ἐπιμέρους κλώνους τοῦ 3ου τμήματος τοῦ κορμοῦ. Ἡ συνολικὴ ἐνέργεια τοῦ γίνεται φ⁴.
Ἡ ὑπολειπόμενη πλεονάζουσα φ³ ἐνέργεια τηρεῖ τὶς προϋποθέσεις γιὰ τὸν σχηματισμὸ τοῦ 4ου τμήματος τοῦ κορμοῦ τοῦ δέντρου, ποὺ θὰ ἀποτελεῖται ἀπὸ 2+1=3 κλαδιὰ μὲ ἐνέργειες φ, 1 καὶ φ ἀντίστοιχα.
9ο βῆμα. Ἡ συνολικὴ ἐνέργεια γίνεται φ⁸ μὲ προσφερόμενη ἐνέργεια ἴση μὲ φ⁶. Αὐτὴ μπορεῖ νὰ ἐπιμεριστεῖ μὲ τὸν παρακάτω τρόπο: φ⁶=φ⁵+φ⁴=(φ⁴+φ³)+(φ³+φ²)
Προσφερόμενη μὲ τὴν ἴδια σειρὰ στὰ τμήματα τοῦ κορμοῦ ξεκινώντας ἀπὸ χαμηλά, καὶ ἐκ νέου διαχωριζόμενη στοὺς κλώνους τοῦ 3ου καὶ 4ου τμήματος, μὲ τὸν ἴδιο τρόπο, συνεισφέρει στὴν αὔξηση τοῦ ὄγκου τους μὲ ἐπιμέρους τελικὲς τιμὲς φ⁶, φ⁵ καὶ φ⁴ ἀντίστοιχα.
10ο βῆμα. Ἡ συνολικὴ ἐνέργεια γίνεται φ⁹. Ἡ προσφερόμενη ἐνέργεια θὰ εἶναι ἴση μὲ φ⁷. Αὐτὴ διαχωρίζεται μὲ τὸν ἑξῆς τρόπο: φ⁷=φ⁶+φ⁵=(φ⁵+φ⁴)+(φ³+φ⁴)
Τὰ δύο πρῶτα ἐνεργειακὰ πακέτα προσφέρονται στὰ δύο πρῶτα τμήματα τοῦ κορμοῦ αὐξάνοντας ὄγκο καὶ ἐνέργεια μὲ τιμὲς φ⁷ καὶ φ⁶ ἀντίστοιχα.
Ἡ φ³ ἐνέργεια δίνεται στὸ 4ο τμῆμα τοῦ κορμοῦ ποὺ ἀναλόγως ἐπιμερισμένο αὐξάνει τοὺς ὄγκους τῶν ἀντίστοιχων κλώνων, ποὺ τώρα συνολικὰ ἔχουν ἐνέργεια ἴση μὲ φ⁵.
Ἡ ὑπολειπόμενη πλεονάζουσα φ⁴ ἐνέργεια τηρεῖ τὶς προϋποθέσεις γιὰ τὸν σχηματισμὸ τοῦ 5ου τμήματος τοῦ κορμοῦ τοῦ δέντρου, ποὺ θὰ ἀποτελεῖται ἀπὸ (2+1)+2=5 κλαδιὰ μὲ ἐνέργειες ((φ,1),φ)(φ,1) ἀντίστοιχα.
11ο βῆμα. Ἡ ἐνέργεια γίνεται ἴση μὲ φ¹⁰ καὶ ἡ προστιθέμενη φ⁸ ἐνέργεια συνεισφέρει μόνο στὴν κατ’ ὄγκο αὔξηση συνολικὰ τοῦ κορμοῦ, καὶ πάλι μὲ συγκεκριμένα, κβαντισμένα ἐπιμέρους ἐνεργειακὰ πακέτα.
12ο βῆμα. Ἡ ἐνέργεια γίνεται ἴση μὲ φ¹¹ καὶ ἡ προστιθέμενη ἐνέργεια εἶναι φ⁹.
Αὐτὴ ἐπιμερίζεται ὡς ἑξῆς: φ9=φ8+φ7=(φ7+φ6)+(φ6+φ5)
Τὰ τρία πρῶτα ἐνεργειακὰ πακέτα προσφέρονται γιὰ τὴν αὔξηση τοῦ ὄγκου τοῦ 1ου , τοῦ 2ου καὶ τοῦ 4ου τμήματος τοῦ κορμοῦ.
Ἡ ὑπολειπόμενη πλεονάζουσα φ5 ἐνέργεια τηρεῖ τὶς προϋποθέσεις γιὰ τὸν σχηματισμὸ τοῦ 6ου τμήματος τοῦ κορμοῦ τοῦ δέντρου, ποὺ θὰ ἀποτελεῖται ἀπὸ (2+1)+2+(2+1)=8 κλαδιὰ μὲ ἐπιμέρους ἐνέργειες ((φ,1),φ)(φ,1) ((φ,1),φ) ἀντίστοιχα.
Ἡ διαδικασία αὐτὴ μπορεῖ νὰ συνεχιστεῖ ἕως ὅτου τὸ φαινόμενο νὰ ὁλοκληρωθεῖ.
Ὁ ἀριθμὸς τῶν κλώνων τοῦ κορμοῦ τοῦ δέντρου, σὲ κάθε ὁρατὸ στάδιο ἀνάπτυξής του ἀκολουθεῖ τὴ σειρὰ Fibonacci.
Εἶναι σημαντικὸ νὰ παρατηρήσουμε ὅτι οἱ ἐνεργειακὲς τιμὲς εἶναι ἀπολύτως προκαθορισμένες καὶ προκύπτουν σὰν γινόμενα τῶν δύο γενεσιουργῶν καὶ ἐλάχιστων τιμῶν 1 καὶ φ μὲ δυνάμεις τοῦ ἀριθμοῦ φ (1,φ,φ²,φ³,…), ὅπως τὸ εἴδαμε καὶ μὲ τοὺς λησμονημένους κατὰ φ μουσικοὺς ρυθμούς.
Εἶναι ἐπίσης σημαντικὸ νὰ παρατηρήσουμε ὅτι τὸ κάθε στάδιο ἐξέλιξης ὁλοκληρώνεται ἐπακριβῶς μὲ τὴν ἐνέργεια ποὺ τοῦ προσφέρεται, χωρὶς νὰ ἀφήνει ἔλλειμμα ἢ πλεόνασμα. Ἔτσι λειτουργεῖ ἡ Φύση γενικώτερα, μέσα ἀπὸ κανόνες ἀπόλυτης ἁρμονίας καὶ οἰκονομίας.
Εἶναι προφανὲς ὅτι ἡ ἀνάπτυξη τοῦ δέντρου εἶναι ἕνα ἀκόμη ἐνδεικτικὸ παράδειγμα φυσικοῦ ἐξελικτικοῦ φαινομένου ποὺ ἀκολουθεῖ τὴν ἀνάπτυξη τῆς ἀκολουθίας τοῦ ἀριθμοῦ φ. Ὅταν ὅμως τὴν ἐξέλιξη τοῦ φαινόμενου τὴν ἀνάγουμε σὲ ἀκέραιες τιμές, μετρώντας τοὺς ἀριθμοὺς τῶν κλώνων, τότε ἡ ἀκολουθία φ στὴ Φύση ἁπλῶς προσαρμόζεται. Ὁ ἀριθμὸς φ παίρνει τὴν ἀμέσως μικρότερη ἀκέραια τιμή, δηλαδὴ τὴν μονάδα καὶ ἔτσι τὸ ἐξελικτικὸ φαινόμενο, μὲ τὴ μέθοδο ποὺ τὸ παρατηροῦμε ἀκολουθεῖ τὴν σειρὰ Fibonacci.
Στὸ δέντρο μας, ἕνα ὅμοιο ἢ παρόμοιο φαινόμενο ἐξελίσσεται καὶ πρὸς τὰ κάτω μὲ τὸ ριζικὸ σύστημα του.
Θὰ μποροῦσε νὰ ὑπάρχει ἕνα ἁπλὸ γεωμετρικὸ σχῆμα ποὺ νὰ ἐξηγεῖ καὶ νὰ ὁριοθετεῖ τὸ φαινόμενο;
Θὰ μποροῦσε αὐτὸ τὸ σχῆμα νὰ εἶναι τὸ χρυσὸ τρίγωνο, δηλαδὴ ἕνα ἰσοσκελὲς τρίγωνο μὲ βάση ἴση μὲ τὸ ὕψος πρὸς αὐτήν;
Θὰ μποροῦσε τὸ διπλὸ χρυσὸ τρίγωνο νὰ ταυτιστεῖ μὲ τὴν ἱερὰ διπλὴ Τετρακτύν τοῦ Πυθαγόρα;
Καὶ ἐπειδὴ ὅτι ἰσχύει κάτω ἰσχύει καὶ πάνω, ὅτι ἰσχύει στὴ Γῆ ἰσχύει καὶ στὸ Σύμπαν, θὰ μποροῦσε ὁ ἴδιος μηχανισμὸς νὰ μᾶς ὑποδείξει τὴν δομὴ καὶ λειτουργία τοῦ μεγαλύτερου καὶ σημαντικώτερου φυσικοῦ ἐξελικτικοῦ φαινομένου ποὺ εἶναι ὁ κύκλος ζωῆς τοῦ Σύμπαντος;
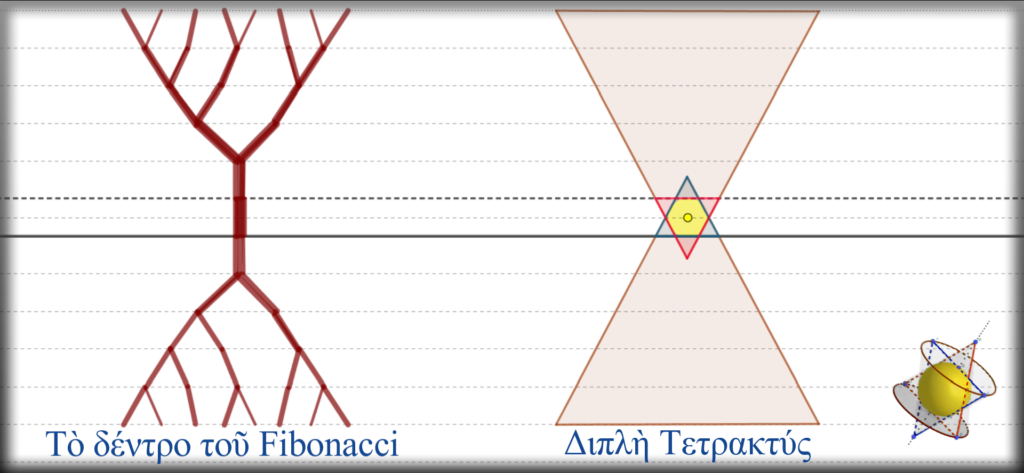
Γιὰ νὰ ἀπαντηθοῦν ὅμως αὐτὰ τὰ ἐρωτήματα χρειάζονται ἐπιπλέον γνώσεις ποὺ στὴν πορεία θὰ μᾶς ἀποκαλυφθοῦν.

