Ὁ τετραγωνισμὸς τοῦ κύκλου στὸ Πὶ καὶ Φί
Ἀκολουθία Φν καὶ περιοδικότητα 12 βημάτων
Ἀπό τὸ βιβλίο…

Εἴδαμε τὴν δυνατότητα ποὺ μᾶς δίνεται νὰ ἀντικαθιστοῦμε τὶς τιμὲς τῶν ὅρων τῆς ἀκολουθίας Φν μὲ τρεῖς ἀκέραιες καὶ ἀπόλυτα καθορισμένες (κβαντισμένες) τιμές, ἀνάλογα μὲ τὶς ἀπαιτήσεις.
Ποιά ἄλλη σχέση ὅμως, πέρα ἀπὸ τὴν προέλευση τους, μποροῦν νὰ ἔχουν αὐτὲς οἱ τρεῖς σειρὲς μὲ τὴν ἀκολουθία τοῦ ἀριθμοῦ φ;
Γιὰ νὰ ἀπαντήσουμε στὸ ἐρώτημα αὐτό, κατασκευάζουμε τὸν ἑπόμενο πίνακα.
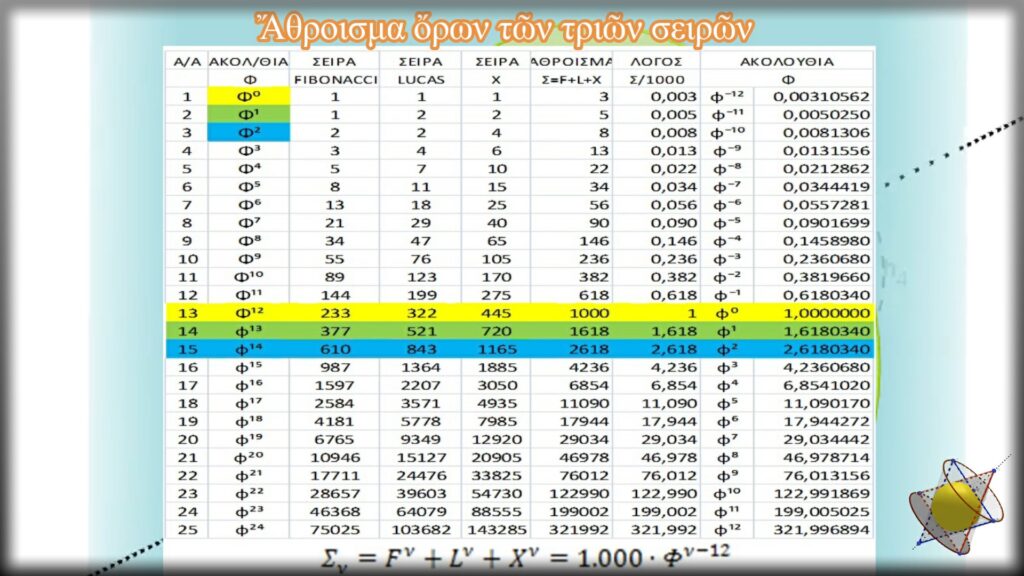
Τοποθετοῦμε στὴν πρώτη στήλη συνεχόμενους ὅρους τῆς ἀκολουθίας Φν ξεκινώντας ἀπὸ τὸν ὅρο φ0=1.
Στὶς ἑπόμενες τρεῖς στῆλες τοποθετοῦμε τὶς τιμὲς τῶν ἀντίστοιχων ὅρων τῶν τριῶν σειρῶν (Fibonacci, Lucas, καὶ Χ).
Στὴν πέμπτη στήλη ὑπολογίζουμε τὸ ἄθροισμα τῶν τιμῶν τῶν ἀντίστοιχων ὅρων τῶν τριῶν σειρῶν.
Ξεκινοῦμε παίρνοντας σὰν ἀφετηρία τὸν ὅρο Φ0=1 τῆς ἀκολουθίας Φν. Μετὰ ἀπὸ 12 (δώδεκα) ἐξελικτικὰ βήματα, φτάνουμε στὸν ὅρο Φ12. Παρατηροῦμε ὅτι τὸ ἄθροισμα τῶν τιμῶν τῶν τριῶν ὅρων τῶν ἀντίστοιχων σειρῶν (F12+L12+X12) εἶναι ἴσο μὲ 1.000. Πρόκειται γιὰ μία τιμὴ ποὺ κεντρίζει τὸ ἐνδιαφέρον καὶ μόνο λόγο τῆς ἀκεραιότητας της. Εἶναι μία τιμὴ κατὰ χίλιες φορὲς μεγαλύτερη ἀπὸ τὴν τιμὴ τοῦ πρώτου ὅρου φ0=1. Γιὰ νὰ τὸ διερευνήσουμε, στὴν ἑπόμενη στήλη διαιροῦμε τὸ ἑκάστοτε ἄθροισμα μὲ τὸν ἀριθμὸ 1.000, ἔτσι ὥστε νὰ μπορέσουμε νὰ βγάλουμε τὰ ὅποια συμπεράσματα.
Εἶναι ἐντυπωσιακό!
Μετὰ ἀπὸ δώδεκα βήματα αὐτοῦ τοῦ ἁρμονικοῦ μαθηματικοῦ μηχανισμοῦ, καταλήγουμε σὲ μία δέκατη τρίτη θέση, στὴν ὁποία τὸ ἄθροισμα τῶν ὅρων τῶν τριῶν σειρῶν εἶναι κατὰ χίλιες φορὲς μεγαλύτερο ἀπὸ τὴν ἀρχικὴ θέση φ0=1.
Γίνεται πιὸ ἐντυπωσιακὸ ὅταν παρατηρήσουμε ὅτι τὸ ἴδιο ἰσχύει γιὰ ὁποιαδήποτε θέση πάρουμε σὰν ἀφετηρία. Μετὰ ἀπὸ δώδεκα ἐξελικτικὰ βήματα, τὸ ἀποτέλεσμα καὶ τὰ συμπεράσματα εἶναι ἀνάλογα. Κάθε φορά, τὸ ἄθροισμα τῶν τιμῶν τῶν ἀντίστοιχων ὅρων τῶν τριῶν σειρῶν, διαιρούμενο μὲ τὸν ἀριθμὸ χίλια, μᾶς δίνει ἀποτέλεσμα ποὺ τείνει στὴν τιμὴ τοῦ ἀρχικοῦ ὅρου τῆς ἀκολουθίας Φν, τοῦ ὅρου ποὺ λάβαμε σὰν ἀφετηρία.
![]()
Φαίνεται λοιπόν, ὅτι ἡ ἀκολουθία, πέρα ἀπὸ τὴν δυνατότητα ποὺ ἔχει νὰ περιγράφει φυσικὰ ἐξελικτικὰ φαινόμενα, παρουσιάζει καὶ μία περιοδικότητα πολὺ συγκεκριμένη, μιὰ περιοδικότητα δώδεκα βημάτων. Φαίνεται ὅτι ἡ ἀκολουθία Φν συμπληρώνει ἕναν πλήρη ἐξελικτικὸ κύκλο σὲ δώδεκα στάδια. Κάθε φορά, ὁ δέκατος τρίτος ὅρος σηματοδοτεῖ τὴν ὁλοκλήρωση ἑνὸς κύκλου καὶ ταυτόχρονα τὴ ἔναρξη ἑνὸς νέου.
Ἀκολουθία ἕτοιμη γιὰ μέτρηση καὶ μικρότερος ὄρος
Ὑπάρχει καὶ κάτι ἀκόμα ποὺ φαίνεται νὰ ἔχει ἐνδιαφέρον. Ὅπως εἶναι γνωστό, ὁ τύπος τῆς Γεωμετρικῆς Προόδου εἶναι : αν=α1λν.
Ἐὰν α1=1 καὶ λ=φ τότε προκύπτει ἡ ἀκολουθία τοῦ ἀριθμοῦ Φ ὅπως ἔχουμε δεῖ. Ἔτσι α0=1, α1=φ, α2=φ2… Ἡ ἀκολουθία ὅμως, μπορεῖ νὰ πάρει τιμὲς καὶ γιὰ ἀρνητικὲς ἀκέραιες τιμὲς τοῦ ἀριθμοῦ ν. Σὲ αὐτὴ τὴν περίπτωση, προκύπτουν οἱ ὅροι φ-1, φ-2, φ-3 … οἱ ὁποῖοι εἶναι μικρότεροι τῆς μονάδας καὶ τείνουν στὸ μηδὲν καθὼς ὁ ἀριθμὸς ν τείνει στὸ -∞.
Εὔλογο ἐρώτημα.
Σὲ ἕνα ἐξελικτικὸ φαινόμενο, ποὺ μπορεῖ νὰ περιγραφτεῖ μὲ τὴν ἀκολουθία Φν. ποιός μπορεῖ νὰ εἶναι ὁ μικρότερος καὶ ἑπομένως καὶ ὁ πρῶτος ὅρος τῆς ἀκολουθίας, ὁ ὁποῖος νὰ ἔχει οὐσιαστικὰ μετρήσιμο νόημα στὸ χῶρο ὅπου κινούμαστε (Εὐκλείδειο ἢ ὄχι);
Αὐθαίρετα θεωρήσαμε σὰν ἀφετηρία τὸν ὅρο φ0=1. Αὐτός, ὅπως εἴπαμε, δὲν εἶναι ὁ μικρότερος.
Ὑπάρχει μιὰ ἰσχυρὴ ἔνδειξη, ποὺ μπορεῖ νὰ θεωρηθεῖ ἱκανὴ στὸ νὰ ὁρίσει τὸν μικρότερο μὲ ὑπολογιστικὴ ἀξία ὅρο στὴ συγκεκριμένη ἀκολουθία.
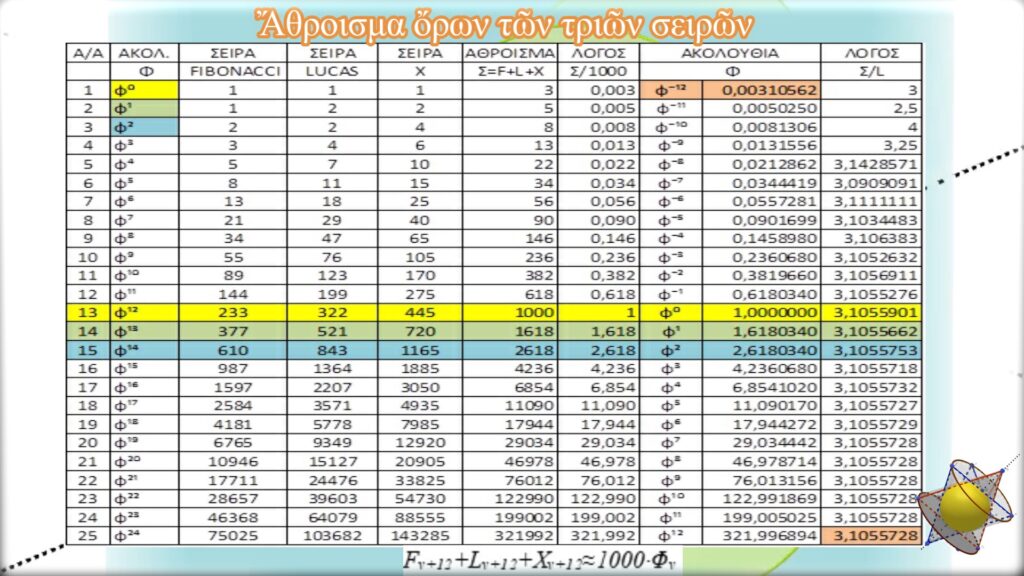
Σὲ κάθε σειρὰ τοῦ πίνακα βρίσκουμε τὸ λόγο τοῦ ἀθροίσματος τῶν ὅρων τῶν τιμῶν τῶν τριῶν σειρῶν (Σν=Fν+Lν+Χν) πρὸς τὴν τιμὴ τοῦ ἀντίστοιχου ὅρου τῆς σειρὰς Lucas, Σν/Lν. Παρατηροῦμε ὅτι ὅσο προχωροῦμε, τόσο ὁ λόγος αὐτὸς τείνει στὴν τιμὴ 3,10557… Ἡ τιμὴ ὅμως αὐτή, ἐὰν διαιρεθεῖ μὲ τὸν ἀριθμὸ 1000, μᾶς δείχνει τὴν τιμὴ τοῦ ὅρου φ-12≈0,00310562… Ἴσως λοιπόν, ὁ ὅρος φ-12 νὰ μπορεῖ νὰ θεωρηθεῖ σὰν ὁ μικρότερος μὲ ὑπολογιστικὴ ἀξία ὅρος, ὁ ὁποῖος καὶ νὰ ἔχει μετρήσιμο νόημα σὲ ἕνα ἐξελικτικὸ φαινόμενο. Ἂς δεχθοῦμε αὐτὴν τὴν προτροπὴ ὡς ἀποδεκτὴ καὶ ἂς δοῦμε ποὺ θὰ μᾶς ὁδηγήσει.
Μιὰ σημαντικὴ λεπτομέρεια. Ἡ τιμὴ ποὺ βρήκαμε, πλησιάζει πάρα πολὺ τὴν τιμὴ τοῦ ὅρου φ-12, δὲν ταυτίζεται ὅμως μὲ αὐτήν.
Ποιά εἶναι ἡ ἀκριβὴς τιμὴ στὴν ὁποία ὁ συγκεκριμένος λόγος τείνει;
Εἴδαμε ὅτι ἡ σειρὰ Lucas στὴν οὐσία εἶναι ἡ ἀκολουθία τοῦ ἀριθμοῦ Φ στρογγυλοποιημένη. Ἐπίσης, εἴδαμε ὅτι ἀπὸ τὴ σειρὰ Lucas θὰ μπορούσαμε νὰ μεταπηδήσουμε στὴ σειρὰ Fibonacci (ἐδῶ) διαιρώντας τὴν τιμὴ τοῦ κάθε ὅρου της μὲ τὸν ἀριθμὸ 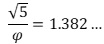
καὶ στὴ σειρὰ Χ (ἐδῶ) πολλαπλασιάζοντας μὲ τὸν ἴδιο ἀριθμὸ καὶ μετὰ νὰ στρογγυλοποιήσουμε τὸ ἀποτέλεσμα στὸν πιὸ κοντινὸ ἀκέραιο. Τὸ ἰδανικὸ σενάριο θὰ λέγαμε ὅτι συμβαίνει σὲ ἀκραῖες συνθῆκες, ὅπου ὁ ἀριθμὸς ν τείνει στὸ ἄπειρο. Τότε, μποροῦμε νὰ ποῦμε ὅτι ἡ τιμὴ τοῦ ὅρου Φν ταυτίζεται μὲ τὴν τιμὴ τοῦ ἀντίστοιχου ὅρου Lν . ![]()
Ἀντίστοιχα θὰ ἔχουμε: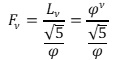
καὶ 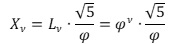
Ἀθροίζουμε τὶς τρεὶς αὐτές τιμές.
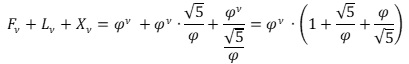
Διαιρούμε τὸ ἄθροισμα μὲ τὸν ὅρο Lν=φν τῆς ἀκολουθίας
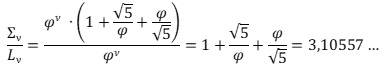
καὶ αὐτό, μὲ τὸν ἀριθμὸ 1.000. Τὸ ἀποτέλεσμα εἶναι σταθερὸ καὶ ἔχει τὴν τιμὴ 0,00310557 γιὰ ν=∞.
Τὸ πάρα πολὺ ἐνδιαφέρον δὲν εἶναι ἡ ἴδια ἡ τιμή, ἡ ὁποία εἶναι πολὺ κοντὰ στὴν τιμὴ τοῦ ὅρου φ-12 , κάτι ποὺ τὸ ἀναμέναμε, ἀλλὰ ἡ ἀπόκλιση.
Αὐτή εἶναι:

Θὰ θυμηθούμε τὸν λόγο 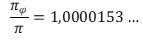
Στὸν λόγο λ ἀποδεδειγμένα φτάσαμε μὲ τὴ χρήση τῶν τριῶν θυγατρικῶν σειρῶν τῆς ἀκολουθίας Φ, τῶν ὁποίων οἱ ὅροι τους παίρνουν μόνο ἀκέραιες τιμές, δηλαδὴ ἄμεσα μετρήσιμες, ἀλλὰ καὶ τῆς ἀκολουθίας Φ τῆς ὁποίας οἱ ὅροι της ἔχουν ἄρρητες τιμές. Ἀντίστοιχα, ὁ λόγος πφ/π, ποὺ σχεδὸν ταυτίζεται μὲ τὸν προηγούμενο λόγο λ, προέκυψε ἀπὸ τὴ σύγκριση τοῦ γνωστοῦ ἀριθμοῦ π, ἀποτέλεσμα μαθηματικῶν προσεγγίσεων στὸν τρισδιάστατο μετρήσιμο χῶρο ὅπου κινούμαστε, καὶ τοῦ ἄρρητου ἀριθμοῦ πφ, δηλαδὴ τῆς τιμῆς τοῦ ἀριθμοῦ π ποὺ προκύπτει μὲ τὴ χρήση τῆς χρυσῆς ἀναλογίας ποὺ ἡ Φύση χρησιμοποιεῖ σὲ ὁποιαδήποτε κλίμακα, ἀκόμα καὶ σὲ συμπαντικὲς ἐφαρμογὲς ὅπου εἶναι πιὸ ἐμφανὴς ἡ ὕπαρξη τῶν τεσσάρων διαστάσεων.
Τὸ Σύμπαν μας ὅμως εἶναι μαθηματικό. Οἱ λόγοι ποὺ προέκυψαν εἶναι μαθηματικοὶ καὶ προέκυψαν μὲ διαφορετικὲς διαδρομές, ποὺ μᾶς δείχνουν ὅμως τὴν κοινὴ τοὺς ἀφετηρία.
Τί μπορεῖ νὰ δηλώνει ὁ λόγος πφ/π;
Ἡ ἐξήγηση του θὰ μᾶς δώσει τὶς πιὸ συναρπαστικὲς ἀπαντήσεις σὲ ὅσα ἡ ἐπιστήμη ἀναζητᾶ ἐπὶ αἰῶνες περὶ δομῆς καὶ λειτουργίας τοῦ σημαντικώτερου ἐξελικτικοῦ φαινομένου, τοῦ Σύμπαντος.
Ἡ ἐξήγησή του θὰ μᾶς δώσει καὶ μία σχέση, καθαρή, χωρὶς μονάδες, μία θεμελιώδη συμπαντικὴ σχέση ὅπου νὰ μπορεῖ νὰ στηριχθεῖ πάνω της ἡ ἑνοποιημένη ἀπόδοση τῶν πάντων, δηλαδὴ τοῦ Ἑνός. Ὅλα αὐτὰ θὰ μᾶς ἀποκαλυφθοῦν στὶς ἑπόμενες σελίδες…
Σύνοψη συμπερασμάτων γιὰ τὴν ἀκολουθία Φν
Συνοψίζοντας ἐπιγραμματικὰ μερικὲς ἀπὸ τὶς μοναδικὲς ἰδιότητες τῆς ἀκολουθίας Φν=φν ποὺ ἐδῶ μᾶς ἐνδιαφέρουν, μποροῦμε νὰ ποῦμε ὅτι
- ἔχει τὴ δυνατότητα νὰ περιγράψει ἁρμονικὰ φαινόμενα ποὺ ἐξελίσσονται κλιμακούμενα στὸ ἄπειρο μὲ ἀπολύτως συγκεκριμένες τιμὲς (κβαντισμένες)
- ἔχει τὴν τάση, οἱ ὅροι της νὰ πάρουν ἀκέραιες τιμές, χωρὶς ὅμως αὐτὸ νὰ ἐπιτυγχάνεται
- ὅταν τὸ φαινόμενο ποὺ περιγράφεται πρέπει νὰ ἔχει ἀκέραιες τιμές, τότε αὐτή, μπορεῖ νὰ ἀντικατασταθεῖ μὲ μία ἀπὸ τὶς θυγατρικὲς της σειρὲς (Fibonacci, Lucas, X), ποὺ μποροῦν καὶ στρογγυλοποιούν τὶς τιμὲς της. Τὰ ἐλλείμματα ἢ πλεονάσματα ποὺ σὲ κάθε ἐξελικτικὸ βῆμα δημιουργοῦνται, δὲν χάνονται ἀλλὰ συνυπολογίζονται στὸ ἑπόμενο βῆμα
- φαίνεται νὰ συμπληρώνει ἕνα πλήρη κύκλο μετὰ ἀπὸ Δώδεκα (12) ἐξελικτικὰ βήματα, ἀνεξαρτήτως τοῦ ὅρου ποὺ θεωροῦμε ἀφετηρία. Ὁ τελευταῖος ὅρος της ἀποτελεῖ ταυτόχρονα καὶ τὸν πρῶτο ὅρο ἑνὸς νέου κύκλου
- δείχνει ὅτι κάθε ἐξελικτικὸ τους βῆμα θὰ μποροῦσε νὰ ἀποδοθεῖ, ἢ καὶ νὰ ἐκτελεστεῖ, μὲ τρία ἐνδιάμεσα βήματα (δύο ἐνδιάμεσες θέσεις) ἀπολύτως καθορισμένες
- ὁρίζει μὲ τὸν τρόπο της, τὸν ὅρο της ποὺ πρέπει νὰ λογαριάσουμε σὰν τὸν μικρότερο μὲ ὑπολογιστικὸ ἐνδιαφέρον (φ-12), καθὼς καὶ τὴν ἀπόκλιση ἀπὸ αὐτὸν (1,0000152004621…).
Ἑπομένως, ὁ ἀριθμὸς Δώδεκα μόνο τυχαῖος δὲν εἶναι.
Φαίνεται ὅτι, ἐφόσον ὑπάρχουν Φυσικὰ Ἐξελικτικὰ Φαινόμενα τὰ ὁποῖα ἀκολουθοῦν τὴν Γεωμετρικὴ Πρόοδο τοῦ ἀριθμοῦ Φ, τότε, κάθε φορὰ ποὺ ἐκτελοῦν δώδεκα βήματα, συμπληρώνουν ἕνα πλήρη κύκλο καὶ ταυτόχρονα ἀνοίγουν ἕνα νέο. Ἐφαρμογὴ τοῦ παραπάνω κανόνα βρίσκουμε στὴ Μουσική, ὅπου δώδεκα εἶναι οἱ νότες ποὺ χρειάζονται γιὰ νὰ συμπληρώσουν μιὰ μουσικὴ κλίμακα. Αὐτό, σίγουρα ἀποτελεῖ ἀκόμα μιὰ πολὺ ἰσχυρὴ ἔνδειξη γιὰ τὴ σχέση τῆς μουσικῆς μὲ τὴν ἀκολουθία τοῦ ἀριθμοῦ Φ.
Τυχαῖος δὲν εἶναι οὔτε ὁ ἀριθμὸς Τρία.
Ἐὰν θεωρήσουμε ὅτι οἱ σειρὲς Fibonacci, Lucas καὶ Χ, στὴν οὐσία κάνουν πράξη τὴν «ἐπιθυμία» τῶν ὅρων τῆς ἀκολουθίας Φ νὰ γίνουν ἀκέραιοι ἀριθμοί, τότε γιὰ τὸ κάθε ἐξελικτικὸ βῆμα ὑπάρχει ἡ δυνατότητα διαχωρισμοῦ του σὲ τρία μέρη. Σὲ τρία μέρη μποροῦμε νὰ χωρίσουμε, ὅπως εἴδαμε, τὸ διάστημα, ποὺ τὰ ἄκρα του σὲ μιὰ χορδὴ ὁρίζουν δύο συνεχόμενες νότες (ἐδῶ). Ἔτσι ὁρίζουμε ἀνὰ περίπτωση, δύο ἐνδιάμεσες (μεταβατικὲς) συχνότητες – νότες. Αὐτὸ θὰ μᾶς βοηθήσει ἀπὸ τὴ μιὰ νὰ καταλάβουμε τὸν τρόπο μὲ τὸν ὁποῖο ἡ ἀκολουθία Φ ὁρίζει τὴ μουσικὴ κλίμακα, καὶ ἀπὸ τὴν ἄλλη νὰ δημιουργήσουμε νέες μουσικὲς κλίμακες ἢ ἐνδεχομένως ἁπλῶς νὰ τὶς ἀναδείξουμε πάλι.
Μιὰ σύμπτωση ἄξια ἀναφορᾶς. Ὁ ἀριθμὸς δώδεκα, ὅπως καὶ ὁ ἀριθμὸς τρία, τυγχάνουν ἰδιαίτερης ἐκτίμησης καὶ σεβασμοῦ ἀπὸ λαοὺς ποὺ ἔχουν νὰ ἐπιδείξουν ἱστορικὸ παρελθὸν μὲ βάθος χρόνου.

