Τετρακτύς
Ἡ γνωστὴ Τετρακτύς
Ἀπό τὸ βιβλίο…

Εἶναι γνωστὸ ὅτι ἡ πυθαγόρεια διδασκαλία στηρίζονταν κυρίως στὴν ἀριθμοσοφία, στὴ δύναμη τῶν ἀριθμῶν καὶ στὸν συμβολισμὸ τους. Ἐξέχουσα θέση σὲ αὐτὴ τὴν φιλοσοφία εἶχε ἡ μονάδα, ὁ «ἱερὸς» ἀριθμὸς δέκα καὶ ἡ σχέση τους μὲ τὴ Φύση. Ὁ Πυθαγόρας γνώριζε ἢ παρατήρησε ὅτι τὸ ἄθροισμα τῶν τεσσάρων πρώτων ἀκέραιων ἀριθμῶν ἔδινε ἀποτέλεσμα τὸν ἀριθμὸ δέκα. Ἦταν ὅμως πεπεισμένος ὅτι τὸ ἄθροισμα αὐτὸ ἦταν κάτι πολὺ παραπάνω ἀπὸ μία μαθηματικὴ πράξη. Στηριζόμενος σὲ αὐτὸ τὸ ἄθροισμα, ἐπινόησε τὴν ἱερὰ ὅπως ἀποκαλοῦσαν Τετρακτύν. Μάλιστα τὴν θεωροῦσαν τόσο σημαντικὴ γιὰ τὴ διδασκαλία τους, ὥστε ἐπέβαλαν στοὺς μαθητές, νὰ ὁρκίζονται σὲ αὐτήν.
Τὸ σχῆμα της δὲν μᾶς εἶναι γνωστό, καθὼς δὲν μᾶς ἄφησαν οὔτε ὁ ἴδιος, οὔτε οἱ μαθητὲς του, γραπτὲς μαρτυρίες. Ἑπομένως μόνο εἰκασίες μποροῦμε νὰ κάνουμε περὶ τοῦ σχήματος της. Στηριζόμενοι στὶς πληροφορίες ποὺ καὶ ὁ Θέων ὁ Σμυρναῖος ἔδωσε μέσα ἀπὸ τὸ βιβλίο του «Τῶν κατὰ μαθηματικὸν χρησίμων εἰς τὴν Πλάτωνος ἀνάγνωσιν», ἐρευνητὲς ἔδωσαν τὴ μορφὴ αὐτῆς σὰν σύνολο 10 σφαιρῶν (σχέδιο 1), ἀλλὰ καὶ σὰν ἰσόπλευρο τρίγωνο, μέσα στὸ ὁποῖο σχηματίζονται ἐννέα μικρότερα ἰσόπλευρα τρίγωνα(σχέδιο 2). Ὑπάρχει καὶ μία τρίτη μορφή, αὐτὴ τοῦ λαβδοειδούς διαγράμματος (σχέδιο 3).
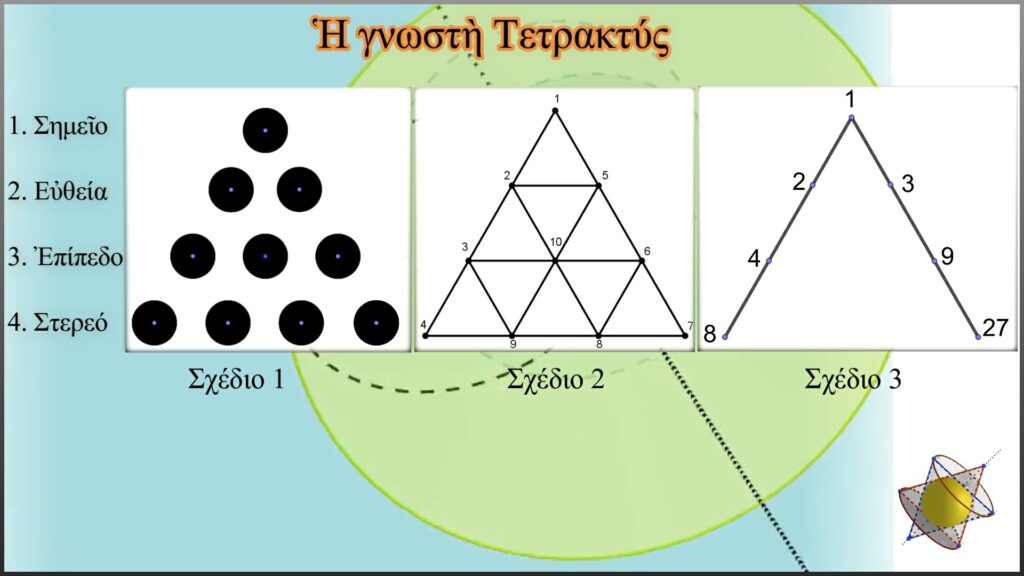
Συνδυασμὸς τῶν προηγούμενων, θὰ μᾶς ἐπέτρεπε νὰ ὑποστηρίξουμε τὴν ὕπαρξη καὶ τῆς ἑπόμενης μορφῆς τῆς Τετρακτύος, προσπαθώντας νὰ ἀναλύσουμε καὶ νὰ δώσουμε μία λογικὴ καὶ μαθηματικὰ ἀποδεδειγμένη ἑρμηνεία στὴ φράση τοῦ Θέωντος περὶ αὐτῆς, ὅτι δηλαδὴ: « τοὺς τε μουσικοὺς καὶ γεωμετρικοὺς καὶ ἀριθμητικοὺς λόγους περιέχουσαι ἐξ ὢν ἡ τοῦ παντὸς ἁρμονία συνέστη».
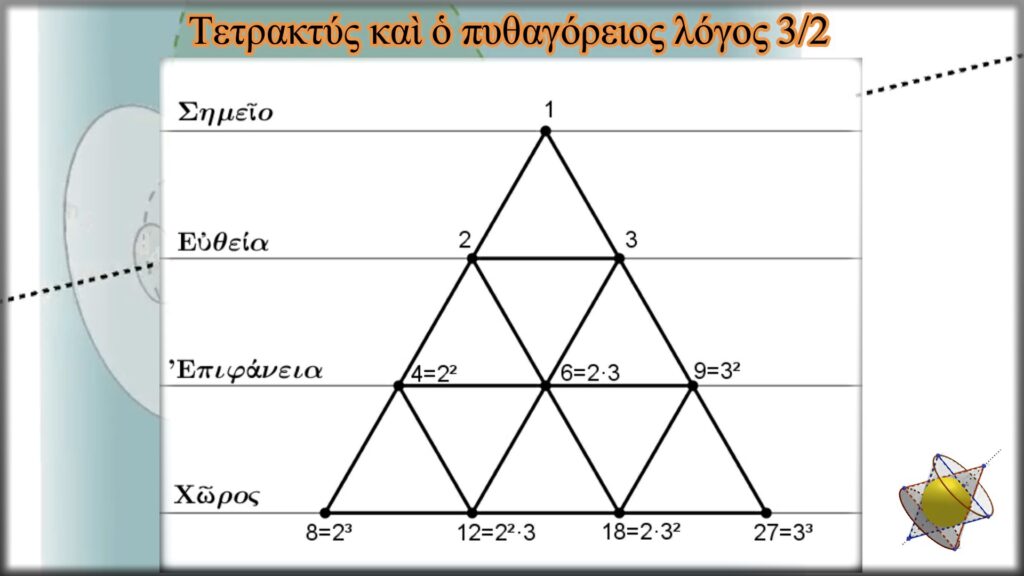
Τὸ σχῆμα της εἶναι καὶ πάλι ἕνα ἰσόπλευρο τρίγωνο. Ἡ κορυφὴ του καθορίζει τὴ μονάδα, τὴν ἀρχή. Στὴ συνέχεια ὁρίζεται ἡ πρώτη διάσταση, ἡ εὐθεία. Σὲ αὐτὴν ἐμφανίζονται οἱ γενεσιουργοὶ ἀριθμοὶ 2 καὶ 3, ἀπὸ τοὺς ὁποίους μποροῦν, μὲ διαδοχικὲς ἀθροίσεις, νὰ προκύψουν ὅλοι οἱ ἀκέραιοι ἀριθμοί. Στὴ ἑπόμενη σειρὰ ὁρίζεται ἡ δεύτερη διάσταση, ἡ ἐπιφάνεια. Οἱ δυνατοὶ συνδυασμοὶ τῶν ἀριθμῶν 2 καὶ 3, γιὰ τὴν ἐπίτευξη ἀποτελέσματος ποὺ νὰ δηλώνει ἐμβαδόν, εἶναι οἱ ἀριθμοὶ αὐτοὶ ὑψωμένοι στὸ τετράγωνο καὶ τὸ γινόμενο 2·3=6. Στὴν τελευταία σειρὰ ὁρίζεται ἡ τρίτη διάσταση, ὁ χῶρος, ὅπου ἔχουμε τοὺς ἀριθμοὺς 2 καὶ 3 ὑψωμένους στὴν τρίτη δύναμη καὶ ὅλους τοὺς δυνατοὺς συνδυασμοὺς αὐτῶν γιὰ τὴν ἐπίτευξη ἀποτελέσματος ποὺ νὰ δηλώνει ὄγκο, τοποθετημένους μὲ αὔξουσα σειρά. Ἔτσι ἔχουμε: 2³=8, 2²·3=12, 2·3²=18 3³=27
Οἱ ἀριθμοὶ δύο καὶ τρία σχηματίζουν καὶ τὸν λόγο 3/2 ποὺ ὁ Πυθαγόρας χρησιμοποίησε γιὰ νὰ δημιουργήση τὴ πρώτη μουσικὴ κλίμακα. Αὐτὸς ὁ λόγος, κυριολεκτικὰ κυριαρχεῖ στὴν Τετρακτύν. Ὅλοι οἱ λόγοι συνεχομένων σημείων ἔχουν τιμὴ 3/2.
Ἔτσι, στὴν πρώτη σειρὰ (εὐθεία), ἔχουμε τὸν λόγο τῶν ἀριθμῶν 3 καὶ 2, ποὺ τὸν ἀποτελοῦν.
Στὴ δεύτερη σειρὰ (ἐπίπεδο) διαδοχικὰ ἔχουμε: 6/4=3/2 ἀλλὰ καὶ 9/6=3/2.
Στὴν τρίτη σειρὰ (χῶρος) εἶναι: 12/8=3/2, 18/12=3/2 καὶ 27/12=3/2.
Σὲ αὐτὴν τὴν μορφὴ τῆς Τετρακτύος, ὁ λόγος 3/2 ἢ 2/3 εἶναι ὁ μοναδικὸς λόγος δύο συνεχόμενων ἀριθμῶν ποὺ βρίσκονται στὴν ἴδια σειρὰ – διάσταση. Φτάνοντας τὴν τελευταία σειρά, παρατηροῦμε ὅτι οἱ ἀριθμοὶ ποὺ τὴν ἀπαρτίζουν σχηματίζουν τοὺς λόγους : 27/18=3/2, 27/12=9/4 και 27/8
Ἂν καθ’ ὑπόδειξη τοῦ Πυθαγόρα θεωρήσουμε ὅτι ἡ συχνότητα τῆς κάθε ἑπόμενης νότας ἰσοῦται μὲ τὰ 3/2 τῆς προηγούμενης, εὔκολα θὰ συμπεράνουμε ὅτι οἱ παραπάνω λόγοι εἶναι οἱ λόγοι ποὺ συνδέουν τρεῖς συνεχόμενες νότες τῆς πυθαγόρειας μουσικῆς κλίμακας, πρὶν τὴν ἀναγωγὴ τους σὲ συχνότητες ἐντὸς διαστήματος ἀρχικῆς ὀκτάβας. Εἶναι μάλιστα αὐτὲς μὲ τὶς ἰσχυρότερες μεταξὺ τους συγγενικὲς σχέσεις (κανόνας τονικότητας στὴν μουσική).
ΝΤΟ,
ΣΟΛ=3/2ΝΤΟ,
ΡΕ2=(3/2)²=9/4ΝΤΟ,
ΛΑ2=(3/2)³=27/8ΝΤΟ
Τέλος, ἁπλὴ ἀναφορὰ θὰ γίνει καὶ στὴν ὕπαρξη τῆς διπλῆς Τετρακτύος, στὴν ὁποία ἀναφέρθηκε καὶ ὁ Θέων ὁ Σμυρναίος. Μιὰ της μορφὴ εἶναι αὐτὴ ποὺ παρουσιάζεται στὸ ἑπόμενο σχέδιο. Πρὸς σύγκριση καὶ γιὰ πρῶτο ἔλεγχο πιθανῆς μεταξύ τους ὄμοιότητας, παρατίθεται μιὰ εἰκόνα σχάσης ἑνὸς σώματος, ἔκρηξης δηλαδὴ ποὺ προέρχεται ἀπὸ τὸ ἐσωτερικὸ του.
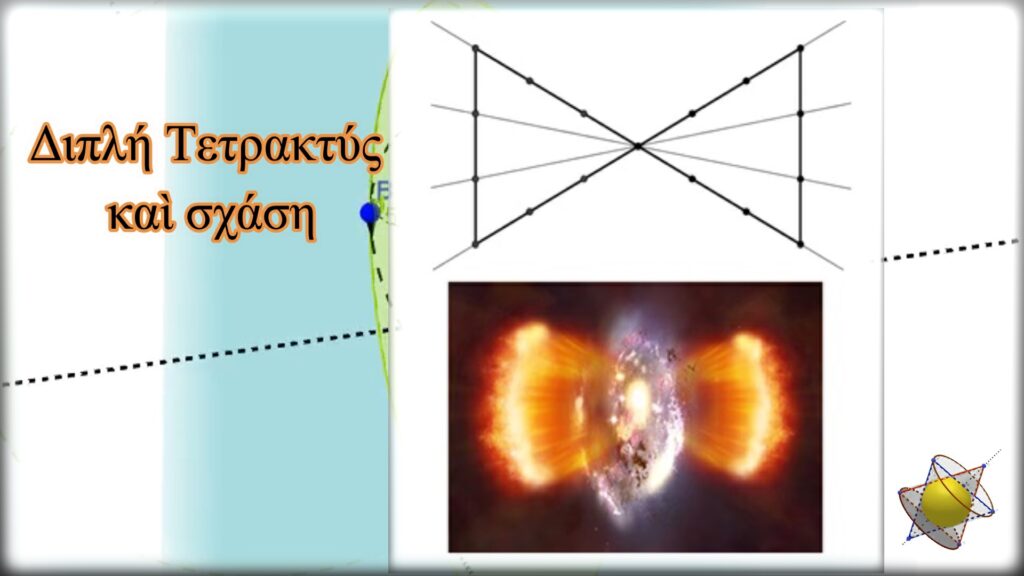
Θὰ ἐπανέλθουμε στὴν διπλὴ Τετρακτὺν στὴν τέταρτη καὶ τελευταία ἑνότητα, ὅπου θὰ δοῦμε τὴν ἄποψη τῆς Τετρακτύος γιὰ τὴν δημιουργία τοῦ Σύμπαντος.

