Τετρακτύς
Τετρακτὺς καὶ ἡ συνύπαρξη τῶν δύο γνωστῶν μουσικῶν θεωριῶν
Ἀπό τὸ βιβλίο…

Στὸ σημεῖο αὐτὸ εἴμαστε ὑποχρεωμένοι νὰ ἀνοίξουμε μιὰ παρένθεση, γιατὶ πρέπει νὰ τονίσουμε κάτι πολὺ σημαντικό. Γιὰ πρώτη φορὰ ἐμφανίζονται οἱ λόγοι 4/3,5/3,5/4,9/8,10/9 Εἶναι λόγοι ποὺ ἐμφανίζονται στὴ μουσικὴ κλίμακα ὅπως προκύπτει ἀπὸ τὰ στάσιμα κύματα καὶ τώρα εἶναι λόγοι ποὺ συναντοῦμε καὶ στὸ συγκεκριμένο γεωμετρικὸ σχῆμα. Εἶναι μιὰ πολὺ σημαντικὴ ἔνδειξη συμβατότητας, τῆς συγκεκριμένης θεωρίας μὲ τὸν δεδομένο μηχανισμό.
Ἐκεῖ εἴδαμε νὰ ἐμφανίζεται ὁ λόγος √(9/8)=1,060660172…. (λόγος πυθαγόρειας μουσικῆς κλίμακας). Ἡ τιμὴ εἶχε προκύψει καὶ σὰν ὁ γεωμετρικὸς μέσος τῶν δύο τιμῶν τῶν μουσικῶν ἡμιτονίων τῆς πυθαγόρειας μουσικῆς κλίμακας, τοῦ μικροῦ ἡμιτονίου 28/35 =1,053498και τοῦ μεγάλου 37/211 =1,067871. Ήταν ἀκόμη μιὰ ἰσχυρὴ ἔνδειξη ὅτι ἡ μουσικὴ κλίμακα θὰ πρέπει νὰ ἀντιμετωπίζεται σὰν γεωμετρικὴ πρόοδος, δηλαδὴ σὰν ἕνα φυσικὸ ἐξελικτικὸ φαινόμενο μὲ σταθερὸ βηματισμό.
Ἀπὸ τὴν ἄλλη, εἴδαμε ὅτι στὴν κλασσική μουσικὴ κλίμακα ἐμφανίστηκαν δύο μουσικοὶ τόνοι,
ὁ μεγάλος τόνος (9/8), ὅπως στὴν περίπτωση ΡΕ/(ΝΤΟ )=(9/8 ΝΤΟ)/ΝΤΟ=9/8 και
ὁ μικρὸς τόνος (10/9), ὅπως στὴν περίπτωση ΜΙ/ΡΕ=(5/4 ΝΤΟ)/(9/8 ΝΤΟ)=10/9
Αὐτὲς τὶς ἀποστάσεις τὶς γεμίσαμε τοποθετώντας ἐνδιάμεσες νότες, τὶς διέσεις. Τὸ πραγματοποιήσαμε πολλαπλασιάζοντας τὴν νότα μὲ τὴν χαμηλότερη συχνότητα μὲ τὴν τιμὴ τοῦ λόγου ἡμιτονίου (16/15) γιὰ τὴ περίπτωση τῶν διέσεων ἢ διαιρώντας τὴν συχνότητα τῆς νότας μὲ τὴν ὑψηλότερη τιμὴ μὲ τὸν ἴδιο λόγο, γιὰ τὴν εὕρεση τῆς ἀντίστοιχης ὕφεσης. Αὐτὴ ὅμως ἦταν μιὰ ἐπιλογὴ ἡ ὁποία μᾶς ὁδήγησε σὲ ἕνα, ἂς ἀναφέρουμε ἀδιέξοδο, ποὺ τὸ προσπεράσαμε μὲ συμβιβασμοὺς (συγκερασματικά). Τὸ πρόβλημα θὰ μποροῦσε νὰ ἀντιμετωπιστεῖ καὶ μὲ τὴ λογικὴ τῆς γεωμετρικῆς προόδου. Ἐὰν γίνονταν αὐτό, τότε ὁ γεωμετρικὸς μέσος τοῦ μεγάλου τόνου (9/8) θὰ ἦταν √(9/8)=1,0606601…και ὁ ἀντίστοιχος γεωμετρικὸς μέσος τοῦ μικροῦ τόνου (10/9) θὰ ἦταν √(10/9)=1,0540925…
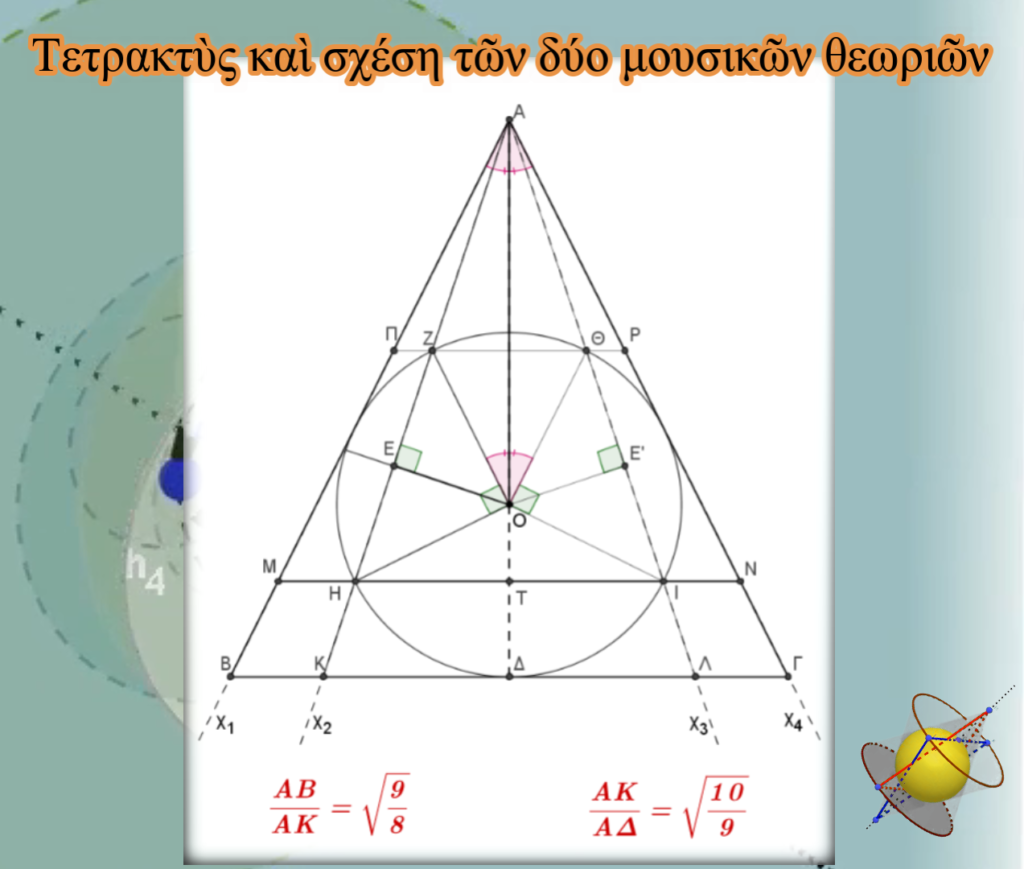
Τὴν τιμὴ √(9/8)=1,0606601… ὅπως εἴδαμε, μᾶς τὴν ἔδωσε ἤδη ὁ μηχανισμὸς σὰν τὸν λόγο ΑΒ/ΑΚ=√(9/8)=1,0606601…Είναι ἡ τιμὴ ποὺ συνδέει τὸν γεωμετρικὸ μηχανισμὸ καὶ τὸ χρυσὸ τρίγωνο, τόσο μὲ τὴν πυθαγόρεια κλίμακα ὅσο καὶ μὲ τὴν κλασσική, ἀρκεῖ νὰ ἀποδεχτοῦμε τὴν ἐμφανὴ αὐτὴ δυνατότητα ἀπόδοσης τῶν τιμῶν τῶν διέσεων.
Γιὰ νὰ γίνει ἀκόμη πιὸ πιστευτὴ αὐτὴ τὴ δυνατότητα, ὁ μηχανισμὸς μᾶς ἔδωσε καὶ τὴν τιμὴ τοῦ δεύτερου γεωμετρικοῦ μέσου, τὴν τιμὴ √(10/9)=1,0540925…
Εἴχαμε ὑπολογίσει τὴν τιμὴ τοῦ εὐθυγράμμου τμήματος , ΑΚ=(√10∙φ)/3 ὁπότε: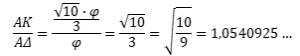
Μέχρι ἐδῶ εἴδαμε τὴ σχέση τῆς Τετρακτύος μὲ τὶς δύο γνωστὲς ἕως σήμερα, μουσικὲς κλίμακες. Στὴ συνέχεια θὰ τὴν δοῦμε νὰ μᾶς ὑποδεικνύει καὶ μία τρίτη, τεράστιας σημασίας μουσικὴ κλίμακα ποὺ στηρίζεται στὸν ἀριθμὸ φ καὶ τὴν ἀκολουθία του.

