Ἡ μελοποιημένη ἀρχαία ἑλληνικὴ ποίηση
Στάσιμα ἐλλειπτικὰ κύματα.
Στάσιμα ἁρμονικὰ κύματα
Ἡ κλασσική φυσικὴ μπόρεσε ἀρκετὰ ἱκανοποιητικὰ νὰ ἑρμηνεύσει τὶς νότες καὶ τὶς μεταξὺ τους σχέσεις, μὲ τὰ στάσιμα κύματα.
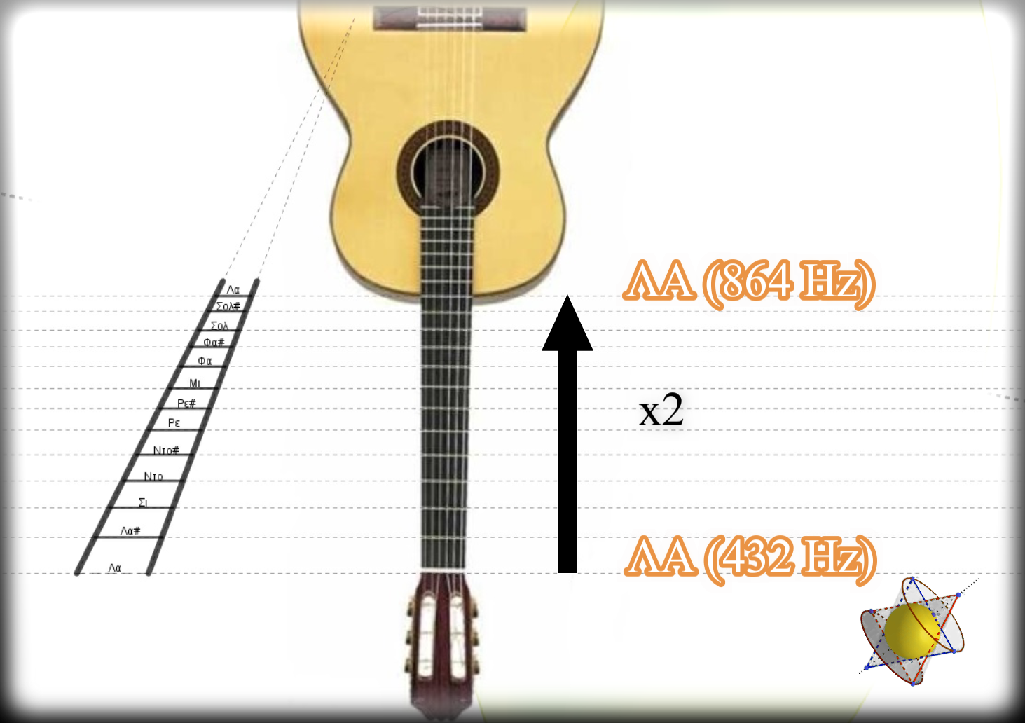
Χορδὴ ποὺ πάλλεται παράγει ἦχο συγκεκριμένης συχνότητας. Ἡ συχνότητα ἐξαρτᾶται καὶ ἀπὸ τὸ μῆκος τῆς χορδῆς. Ὅσο τὸ μῆκος τῆς χορδῆς μειώνεται, τόσο ἡ συχνότητα αὐξάνεται.
Ὅταν μία χορδὴ πάλλεται σχηματίζονται στάσιμα κύματα. Τὸ στάσιμο κύμα τὸ ὁποῖο καλύπτει τὸ συνολικὸ μῆκος τῆς χορδῆς δίνει καὶ τὴν βασική, τὴν θεμελιώδη συχνότητα. Αὐτὴ ὅμως δὲν εἶναι ἡ μοναδική.
Ἡ ἐμφάνιση ἑνὸς δεσμοῦ στὸ μέσον τῆς χορδῆς τὴν χωρίζει σὲ δύο ἴσα μέρη, ὅπου ἐμφανίζονται στάσιμα κύματα διπλάσιας συχνότητας, ἡ δεύτερη ἁρμονική.
Ἡ ἐμφάνιση δύο δεσμῶν, χωρίζει τὴ χορδὴ σὲ τρία ἴσα μέρη, μὲ ἀποτέλεσμα τὴν ἐμφάνιση στάσιμων κυμάτων τριπλάσιας συχνότητας, ἡ τρίτη ἁρμονική, κ.ο.κ.
Ἔτσι, ἐμφανίστηκαν οἱ νότες καὶ ἔτσι δημιουργήθηκε ἡ 12-τονική μουσικὴ κλίμακα. Ἐπειδὴ κλίμακα σημαίνει σκάλα, σκάλα τὴν ὁποία τὴν ἀνεβαίνουμε σκαλί-σκαλί μὲ ἁρμονικὸ τρόπο, τὶς μικρὲς ἀνωμαλίες στὸ βηματισμὸ τὶς διορθώσαμε.
Θελήσαμε, ἡ κάθε ἑπόμενη νότα νὰ ἔχει συχνότητα κατὰ ¹²√2 φορὲς μεγαλύτερη ἀπὸ τὴν συχνότητα τῆς προηγούμενης, ἔτσι ὥστε μετὰ ἀπὸ 12 ἐξελικτικά βήματα, νὰ πάρουμε τὴν ἴδια μὲ τὴν ἀρχικὴ νότα ἀλλὰ κατὰ μιὰ ὀκτάβα πιὸ πάνω, δηλαδὴ νὰ πάρουμε τὴν ἀντίστοιχη νότα διπλάσιας συχνότητας.
Εἶναι ὅμως τὰ στάσιμα κύματα τὰ μοναδικὰ τὰ ὁποῖα ὑπάρχουν;
Μήπως ὑπάρχουν καὶ ἄλλης μορφῆς στάσιμα κύματα, τὰ ὁποῖα θὰ μποροῦσαν νὰ μᾶς ὑποδείξουν νέες, ὑπαρκτές, καὶ παράλληλα φυσικὲς νότες;
Γεωμετρικὸς μηχανισμὸς 1ου σταδίου - Τετραγωνισμὸς τοῦ κύκλου;
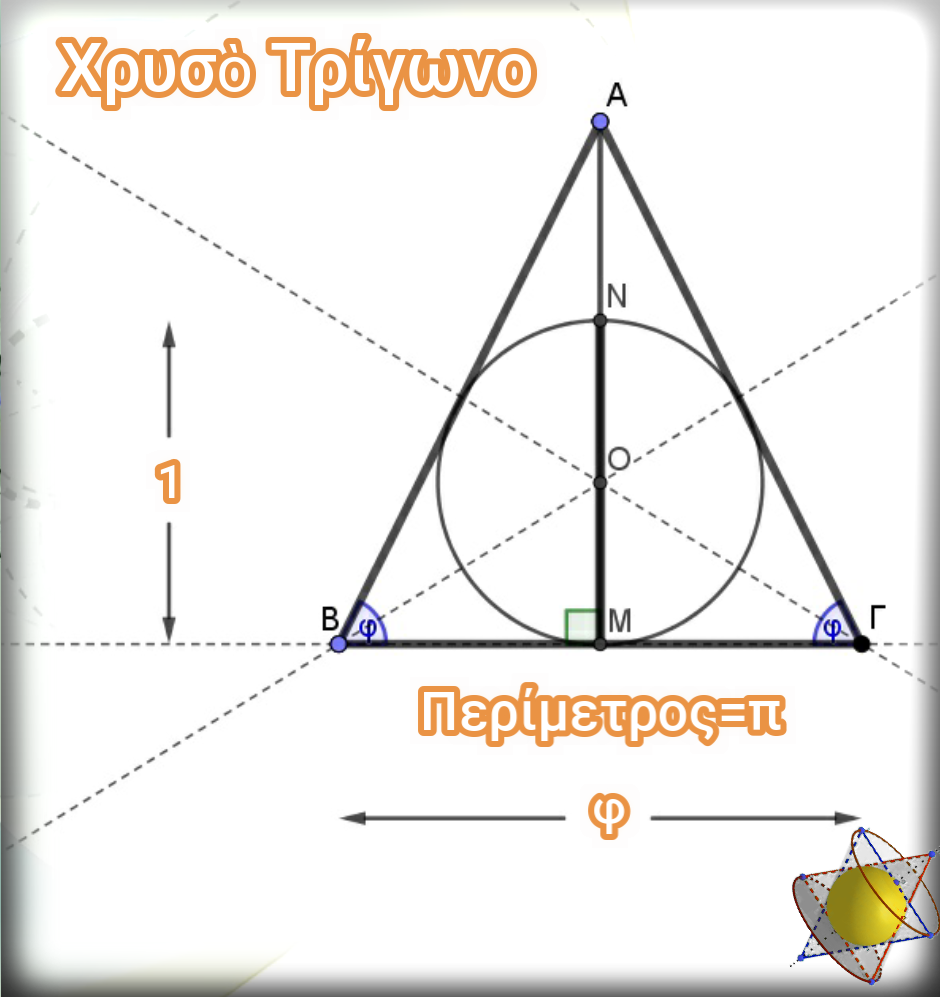
Στὸ πρῶτο μέρος τῆς παρουσίασης εἴδαμε μὲ ποιὸ τρόπο εὔκολα καὶ γρήγορα μποροῦμε νὰ βροῦμε τὴν χρυσὴ τομὴ ἑνὸς εὐθυγράμμου τμήματος. Μέσα ἀπὸ αὐτὴ τὴν κατασκευὴ ἐμφανίστηκε ἕνα ἰδιαίτερο ἰσοσκελὲς τρίγωνο τοῦ ὁποίου ἡ βάση του εἶναι ἴση μὲ τὸ ὕψος πρὸς αὐτήν. Τὸ τρίγωνο αὐτὸ τὸ ὀνομάσαμε Χρυσὸ τρίγωνο γιατὶ ἂν καὶ δὲν φαίνονται, ὑπάρχουν σὲ αὐτὸ ὅλες οἱ ἀναλογίες τῆς χρυσῆς τομῆς. Ἐὰν μάλιστα θεωρηθῆ ὅτι ἡ βάση του εἶναι ἴση μὲ τὸν
ἀριθμὸ φ, τότε ἀποδεικνύεται ὅτι ἡ διάμετρος τοῦ ἐγγεγραμμένου σὲ αὐτὸ κύκλου εἶναι ἴση μὲ τὴν μονάδα, ὁπότε καὶ ἡ περίμετρος του εἶναι ἴση μὲ τὸν ἀριθμὸ π. Εἶναι τὸ πιὸ ἁπλὸ γεωμετρικὸ σχῆμα καὶ ἐνδεχομένως τὸ μοναδικὸ στὸ ὁποῖο ἐμφανίζονται ταυτόχρονα οἱ δύο αὐτοὶ σημαντικώτατοι ἀριθμοί, ὁ ἀριθμὸς π καὶ ὁ ἀριθμὸς φ.Ἔμενε νὰ βροῦμε καὶ ποιὰ εἶναι ἡ μεταξὺ τους σχέση.
Ἡ περαιτέρω ἀνάπτυξη τῆς συγκεκριμένης κατασκευῆς, μᾶς ἔδωσε τρία συνεχόμενα εὐθύγραμμα τμήματα μὲ ἀναλογίες Φ καὶ κάθετα μεταξὺ τους, θὰ μπορούσαμε νὰ ποῦμε σὲ μία μαιανδρική διάταξη. Στὴν συνέχεια, μὲ δύο ἁπλὰ βήματα προέκυψε ἕνα εὐθύγραμμο τμῆμα τὸ ὁποῖο βρέθηκε ὅτι εἶναι ἴσο μὲ 6/5φ², ἴσο μὲ 3,1416… Ἡ ἰσχύουσα τιμὴ τοῦ ἀριθμοῦ π εἶναι 3,14159… Ἡ χαρὰ μου, ὅπως μπορεῖτε νὰ φανταστῆτε, ἦταν ἰδιαίτερα μεγάλη γιατὶ ἔστω καὶ προσεγγιστικά, μπόρεσα νὰ τετραγωνίσω τὸν κύκλο.
Ἡ ἀλήθεια ὅμως εἶναι ὅτι αὐτὸ τὸ ὁποῖο προέκυψε ἦταν κάτι πολὺ σπουδαιότερο. Αὐτὸ τὸ ὁποῖο προέκυψε εἶναι ἡ τιμὴ τοῦ ἀριθμοῦ π στὴ συμπαντικὴ του διάσταση, ἐκεῖ δηλαδὴ ὅπου ἐμφανίζεται καὶ ἡ τέταρτη διάσταση τοῦ χρόνου. Μέσα ἀπὸ αὐτὴν τὴν καταρχὴν ἀποδοχή, ἀλλά καὶ τὴν ἑρμηνεία τῆς Τετρακτύος ὅπως μοῦ ἀποκαλύφτηκε, ἄρχισε νὰ ἐμφανίζεται ἕνα κοσμογονικό, μουσικὸ μοντέλο, ἰδιαίτερα πιστικό.
Ἔτσι προέκυψαν καὶ ἑπόμενες δύο ἐξισώσεις. Ἡ τεράστια σημασία τοὺς θὰ φανῆ ὅταν καὶ ἐφόσον αὐτὲς γίνουν ἀποδεκτές. Παντός, στὸ βιβλίο μου «Ἡ χρυσὴ τομὴ στὴν μουσικὴ» ὑπάρχουν ἀρκετὰ στοιχεῖα, ἱκανὰ νὰ ὁδηγήσουνε στὴν ἀποδοχὴ τοῦ συγκεκριμένου συμπαντικοῦ μοντέλου καὶ ταυτόχρονα νὰ ἀνοίξουν νέα δρόμους σκέψης, προβληματισμοῦ, ἀλλὰ καὶ ἔρευνας ποὺ θὰ μπορούσανε νὰ ἐξελίξουνε ἀλλὰ ἐὰν χρειαστῆ καὶ νὰ βελτιώσουνε,ὅσα ἀναγράφονται στὸ βιβλίο μου.
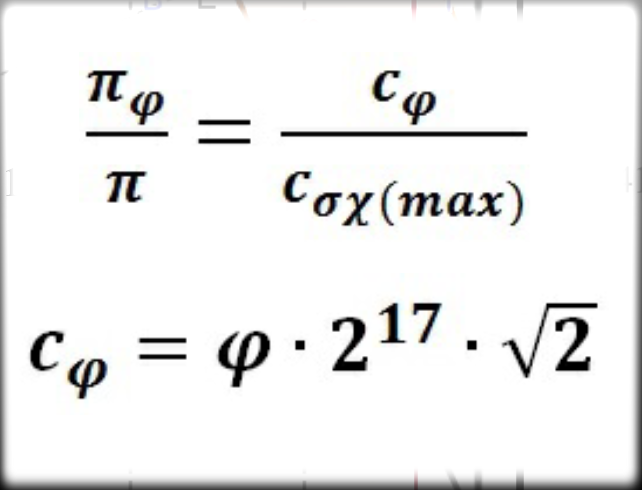
Γεωμετρικὸς μηχανισμὸς 2ου σταδίου - Λόγος ἡμιτονίου
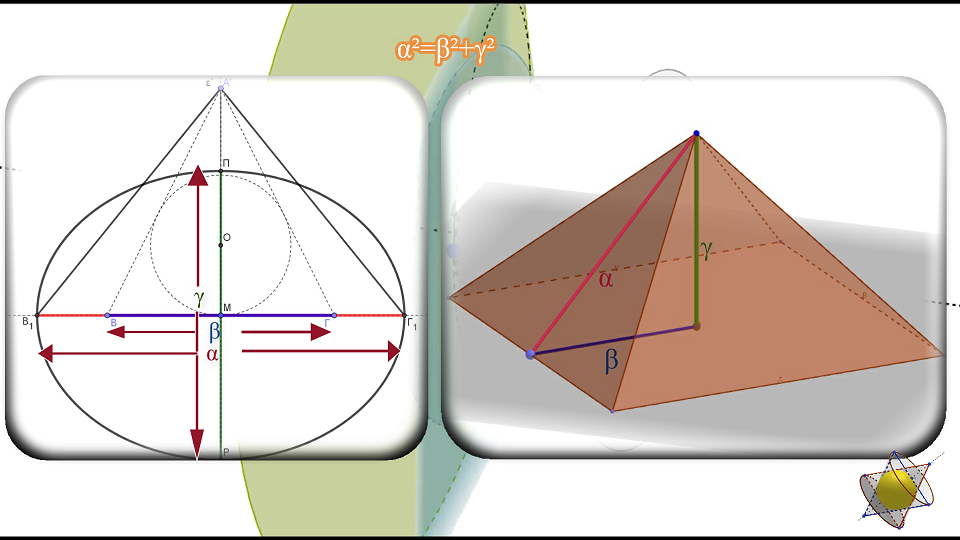
Τὸ δεύτερο στάδιο ἐξέλιξης τοῦ συγκεκριμένου γεωμετρικοῦ μηχανισμοῦ, μοῦ ἔδωσε ἕνα εὐθύγραμμο τμῆμα τὸ ὁποῖο εἶναι ἴσο μὲ φ³/4, ἴσο μὲ 1,059… Ἡ τιμὴ αὐτὴ σχεδὸν ταυτίζεται μὲ τὴν τιμὴ ¹²√2 , δηλαδὴ τὴν τιμὴ τοῦ ἡμιτονίου, τοῦ λόγου συχνοτήτων μεταξὺ δύο διαδοχικῶν νοτῶν τῆς δωδεκατονικῆς μουσικῆς μας κλίμακας. Αὐτὸ τὸ θεώρησα ἰδιαίτερα ἰσχυρὴ ἔνδειξη σχέσης τοῦ ἀριθμοῦ φ καὶ μὲ τὶς τονικὲς ἀξίες. Στὸν ἴδιο μηχανισμὸ ἐμφανίζονται καὶ δύο εὐθύγραμμα τμήματα, τὸ Β₁Γ₁ καὶ τὸ ΒΓ μὲ μεταξὺ τους λόγο ἴσο μὲ τὸν ἀριθμὸ φ, ἀλλὰ καὶ μὲ τέτοια διάταξη ποὺ νὰ ἐπιτρέπη στὰ σημεῖα Β καὶ Γ νὰ ἀποτελοῦν ἑστίες ἔλλειψης μὲ μεγάλο ἄξονα τὸ εὐθύγραμμο τμῆμα Β₁Γ₁.
Τὴν ἔλλειψη αὐτὴ τὴν ὀνόμασα Χρυσὴ ἔλλειψη λόγῳ ἀκριβῶς τῆς ἐμφάνισης τῆς συγκεκριμένης ἀναλογίας, καὶ εἶναι τόσο μοναδικὴ ὅσο μοναδικὴ εἶναι καὶ ἡ μεγάλη πυραμίδα τοῦ Χέοπος, ἡ ὁποία τὶς ἴδιες ἀναλογίες ἀκολουθεῖ.
Ἐὰν τώρα θεωρήσουμε ὅτι τὸ εὐθύγραμμο τμῆμα Β₁Γ₁ εἶναι χορδὴ ποὺ πάλλεται, μήπως ὑπὸ προϋποθέσεις θὰ μπορούσανε νὰ ἐμφανιστοῦν στάσιμα ἐλλειπτικὰ κύματα ΒΓ μὲ ἀναλογία φ;
Ἂν ἰσχύει κάτι τέτοιο πραγματικὰ θὰ ἐπρόκειτο γιὰ μιὰ τεράστια ἀνακάλυψη. Ἔπρεπε νὰ τὸ ἐρευνήσω.
Θὰ πρέπει νὰ σημειωθῆ ὅτι μὲ βάση τὴν μέχρι σήμερα γνωστὴ φυσικὴ καὶ τὰ στάσιμα ἁρμονικὰ κύματα, ἐὰν δὲν ὑπάρχουν ἄλλης μορφῆς στάσιμα κύματα, τότε ἡ ἀμέσως ἑπόμενη συχνότητα ποὺ θὰ ἀκούγεται ὅταν μία χορδὴ πάλλεται θὰ εἶναι ἡ διπλάσια τῆς θεμελιώδους.
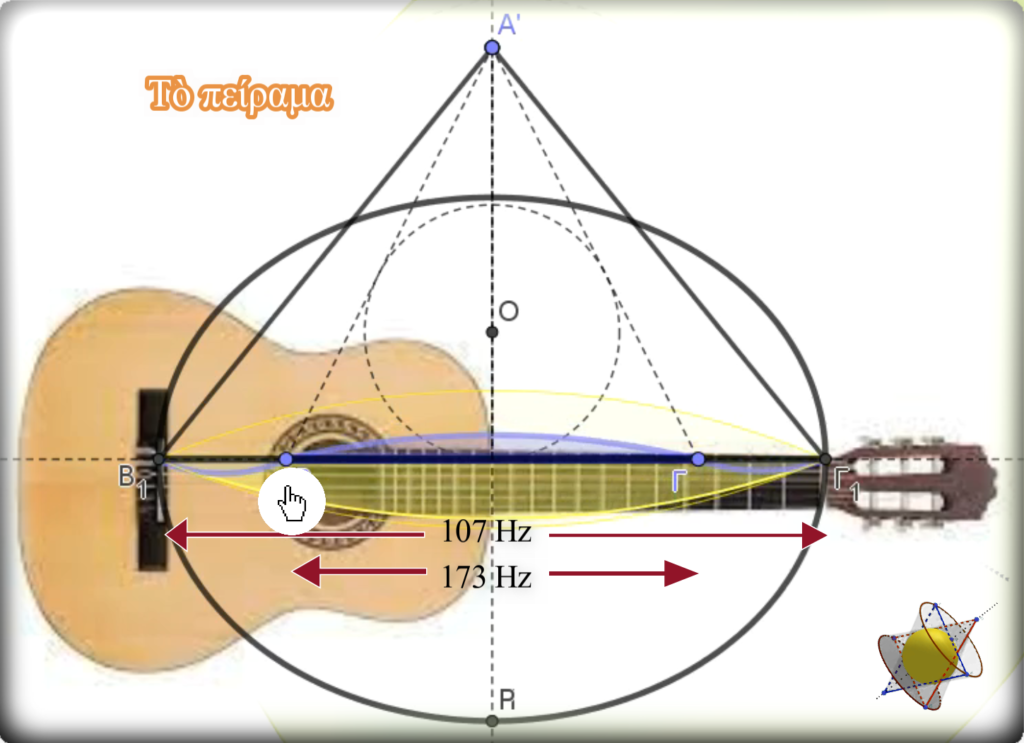
Τό πείραμα
Μὲ τὴ βοήθεια ἀναλυτὴ συχνοτήτων, μετρήθηκε ἡ συχνότητα μὲ τὴν ὁποία ἐλεύθερα πάλλεται μία χορδὴ κιθάρας. Αὐτὴ βρέθηκε ὅτι εἶναι ἴση μὲ 107 Hz.
Στὴ συνέχεια καὶ ἐνῶ ἡ χορδὴ ἐξακολουθοῦσε νὰ πάλλεται, τὴν ἀκουμπήσαμε ἐλαφριὰ σὲ σημεῖο ποὺ θὰ ἀντιστοιχοῦσε στὴ μία ἀπὸ τὶς δύο ἑστίες χρυσῆς ἔλλειψης μὲ μεγάλο ἄξονα ἴσο μὲ τὴ χορδὴ τῆς κιθάρας. Ὁ σκοπὸς μας ἦταν
μὲ αὐτόν τὸν τρόπο νὰ κόψουμε τὰ περισσότερα ἀπὸ τὰ γνωστὰ ἁρμονικὰ κύματα ἐπιτρέποντας τὴν ἐμφάνιση, ἐφόσον ὑπάρχει, ἐλλειπτικοῦ στάσιμου κύματος μὲ λόγο φ. Ἡ συχνότητα αὐτοῦ θὰ ἔπρεπε νὰ εἶναι ἴση μὲ 107*φ Hz, δηλαδὴ θὰ ἔπρεπε νὰ εἶναι ἴση μὲ 173Hz, αὐστηρά.
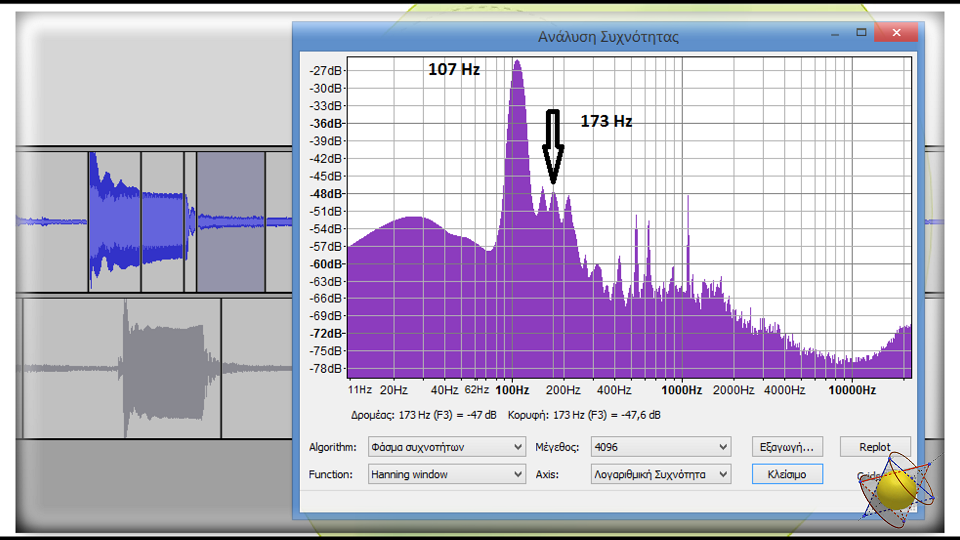
Τὸ ἀποτέλεσμα μᾶς δικαίωσε ἀπόλυτα μὲ τὴν ξεκάθαρη ἐμφάνιση τῆς συγκεκριμένης συχνότητας. Τὸ ὅτι ἡ συχνότητα αὐτὴ εἶναι μικρότερη τῆς διπλάσιας τῆς θεμελιώδους, δηλαδὴ μικρότερη τῶν 214Hz, μᾶς ξεκαθαρίζει πὼς δὲν πρόκειται γιὰ συχνότητα ποὺ ἀντιστοιχεῖ σὲ κλασσικό ἁρμονικὸ κύμα.
Ἡ ἐμφάνιση καὶ δύο ἀκόμη κορυφῶν, δηλαδὴ δύο ἀκόμα συχνοτήτων ἔχει τὴν ἰδιαίτερη σημασία της.
Στὴ συνέχεια θὰ προσπαθήσουμε νὰ συγκροτήσουμε, ἀλλὰ καὶ θὰ ἐξελίξουμε τὴ σπουδαία αὐτὴ ἀνακάλυψη.
Διαδοχικὰ κατὰ φ στάσιμα ἐλλειπτικὰ κύματα
Ἔστω χορδὴ ποὺ πάλλεται ἐλεύθερα, μᾶς δίνει τὴ νότα Λὰ στὰ 432 Hz. Ἡ χορδὴ αὐτὴ θὰ δώση καὶ τὸ δικὸ της στάσιμο ἐλλειπτικὸ κύμα μὲ λόγο φ. Ἡ συχνότητα αὐτοῦ θὰ εἶναι ἴση μὲ 432*φ Hz, δηλαδὴ θὰ εἶναι ἴση μὲ 699 Hz.
Τὸ πρῶτο ἐλλειπτικὸ κύμα μὲ τὴ σειρὰ του θὰ δώση τὸ δικὸ του ἐλλειπτικὸ κύμα, τὸ δεύτερο. Ἡ συχνότητα τοῦ νέου κύματος θὰ εἶναι ἴση μὲ 432*φ² ἢ 699*φ. Τὴν τιμὴ 1131 ποὺ προκύπτει, τὴν διαιροῦμε μὲ τὸ δύο γιὰ νὰ πάρουμε τὴν ἀντίστοιχη συχνότητα ἐντὸς τῶν ὁρίων τῆς μουσικῆς ὀκτάβας ποὺ κινούμαστε, δηλαδὴ ἀνάμεσα στὰ 432 καὶ 864 Hz.
Στὴ συνέχεια, τὸ δεύτερο ἐλλειπτικὸ κύμα, μὲ τὴ σειρὰ του θὰ δώση τὸ δικὸ του ἐλλειπτικὸ κύμα, τὸ τρίτο. Ἡ συχνότητα τοῦ τρίτου ἐλλειπτικοῦ κύματος θὰ εἶναι ἴση μὲ 432*φ³. Τὴν τιμὴ 1830 ποὺ προκύπτει, αὐτὴν τὴν φορὰ θὰ τὴν διαιροῦμε μὲ τὸν ἀριθμὸ 4 γιὰ νὰ πάρουμε τὴν ἀντίστοιχη συχνότητα ἐντὸς τῶν ὁρίων τῆς μουσικῆς ὀκτάβας ποὺ κινούμαστε. Ἔτσι προέκυψε ἡ συχνότητα τῶν 457,5 Hz. Εἶναι ἡ ἴδια τιμὴ ποὺ θὰ πέρναμε και καθ’ ὑπόδειξιν τοῦ γεωμετρικοῦ μηχανισμοῦ ποὺ εἴδαμε προηγουμένως. Ἡ συχνότητα ὅμως αὐτὴ ἀντιστοιχεῖ στὴ νότα Λά#.

Βλέπουμε λοιπὸν ὅτι καὶ πάλι μποροῦμε νὰ πάρουμε τὴν 12-τονική μουσικὴ κλίμακα μὲ φυσικὸ τρόπο, ἀντιμετωπίζοντας ὅμως αὐτὴν τὴν φορὰ τὴν δημιουργία τῶν στάσιμων κυμάτων σὰν νὰ εἶναι ἕνα φυσικὸ ἐξελικτικό φαινόμενο ποὺ βασίζεται στὸν ἀριθμὸ φ καὶ στὴν ἀκολουθία του.
Οἱ ἄλλες δύο συχνότητες οἱ ὁποῖες προέκυψαν βρίσκονται ἀνάμεσα σὲ γνωστὲς νότες. Ἔτσι ἡ συχνότητα τῶν 699 Hz βρίσκεται ἀνάμεσα στὶς Φὰ καὶ Φα#, ἐνῶ ἡ συχνότητα τῶν 565,5 Hz βρίσκεται ἀνάμεσα στὶς νότες Ντὸ# καὶ Ρέ.
Στὴ συνέχεια θὰ δοῦμε ἐὰν αὐτὲς οἱ συχνότητες εἶναι τυχαῖες ἢ ἐὰν λόγῳ τοῦ ὅτι προέκυψαν μέσα ἀπὸ φυσικὲς διαδικασίες, παίρνουν ἀντίστοιχα καὶ συγκεκριμένες τιμές.
