Τετρακτύς καὶ Θεμελιώδης Μουσικὴ Κλίμακα
Γεωμετρικὴ εὔρεση
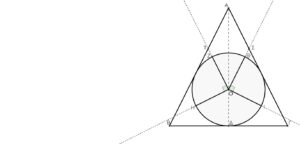
Ἀπό τὸ βιβλίο…

Μηχανισμὸς β΄ σταδίου- Ὁ λόγος τῆς μουσικῆς κλίμακας τοῦ φ
Ἕως τώρα εἴδαμε τὴ σημασία τοῦ ἐγγεγραμμένου μοναδιαίου κύκλου ἐντὸς τοῦ Χρυσοῦ τριγώνου, τόσο στὸν τετραγωνισμὸ τοῦ κύκλου, ὅσο καὶ στὴν Τετρακτύν τοῦ Πυθαγόρα (μηχανισμὸς α΄σταδίου).
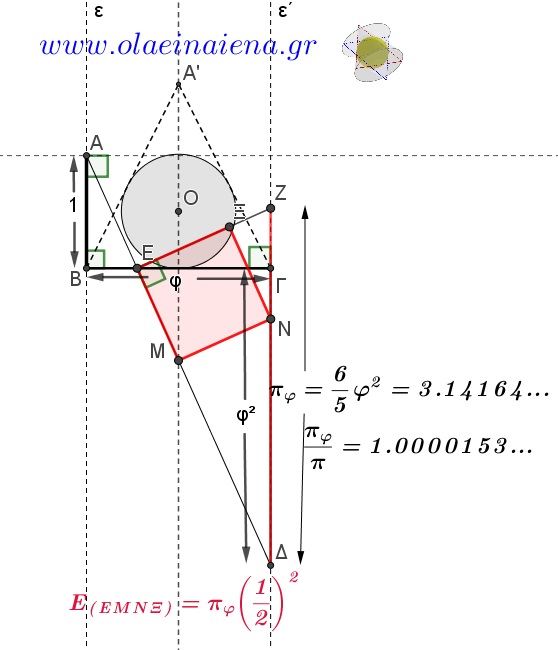
Στὴ συνέχεια θὰ φανεῖ καὶ ἡ βασικὴ του συμμετοχὴ στὴν ἐξέλιξη τοῦ μηχανισμοῦ μας, ὅπως ἐπίσης καὶ στὴν μουσικὴ κλίμακα.
Ἐξ ἀρχῆς ἡ Τετρακτύς μᾶς ἔδωσε τὴν ἀναλογία τῆς χρυσῆς τομῆς σὰν τὸν λόγο τῆς βάσης τοῦ τριγώνου πρὸς τὴν διάμετρο τοῦ ἐγγεγραμμένου κύκλου.
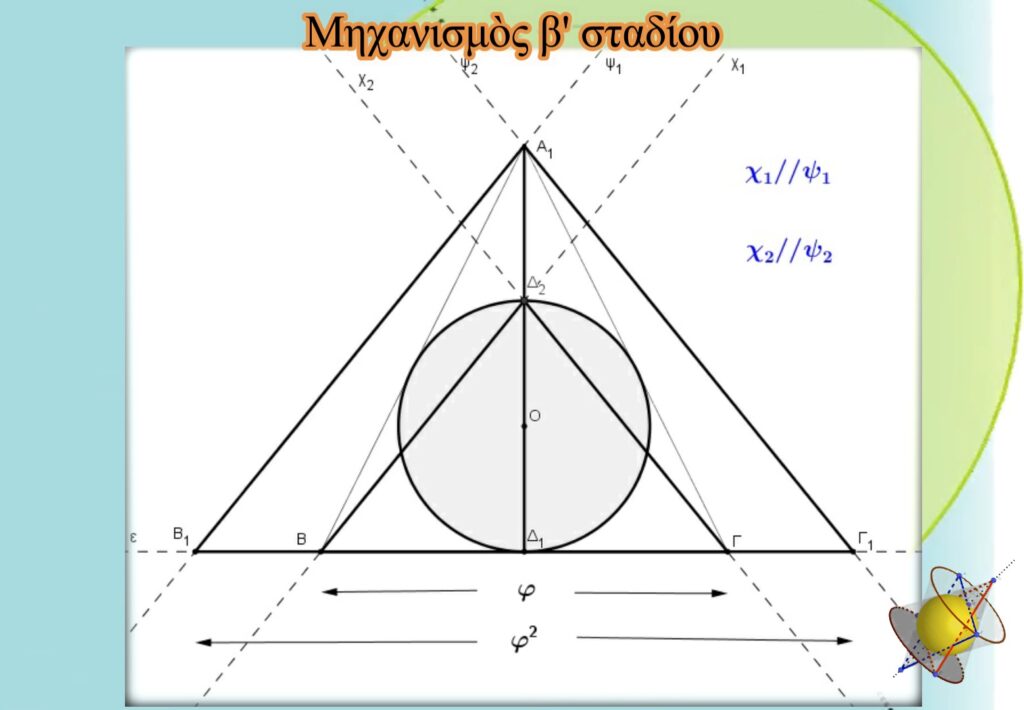
Κατασκευάζουμε τὸ ἰσοσκελὲς τρίγωνο ΒΔ2Γ. Ὁ λόγος βάσης πρὸς ὕψος εἶναι ἴσος μὲ φ, καθὼς τὸ ὕψος Δ1Δ2 εἶναι ἴσο μὲ τὴ διάμετρο τοῦ μοναδιαίου κύκλου καὶ ἡ βάση ΒΓ εἶναι ἴση μὲ φ.
Μὲ τὴν βοήθεια παραλλήλων εὐθειῶν κατασκευάζουμε τὸ τρίγωνο Α1Β1Γ1.
Ἀπὸ τὴν προφανὴ ὁμοιότητα τῶν τριγώνων ΒΔ2Γ καὶ Α1Β1Γ1. προκύπτει ὅτι:
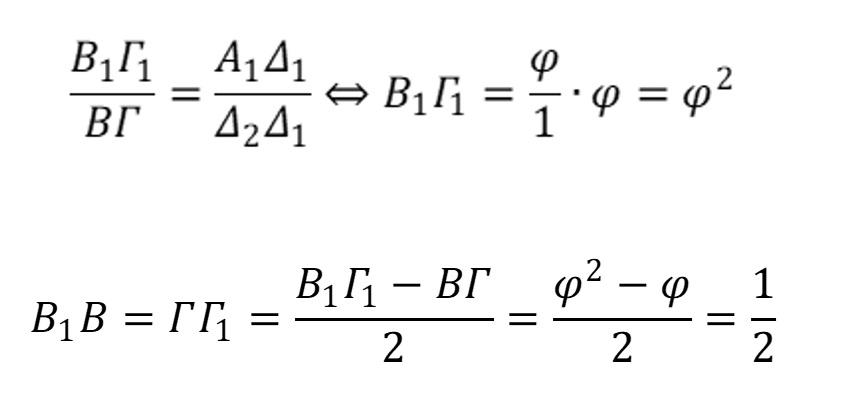
Θὰ ἐξελίξουμε τὸν μηχανισμὸ μὲ μιὰ κατασκευὴ ἀνάλογη αὐτῆς τοῦ τετραγωνισμοῦ τοῦ κύκλου.
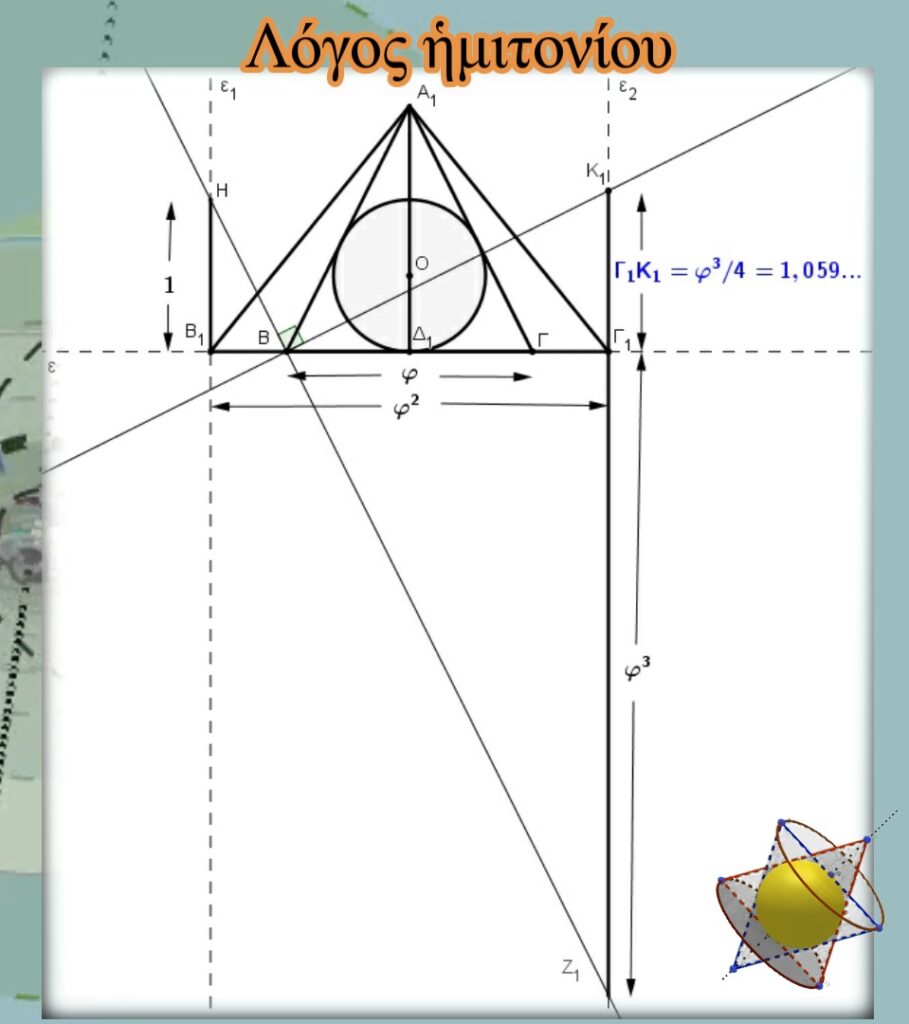
Κατασκευή.
Ἀπὸ τὰ σημεῖα Β1 καὶ Γ1 φέρνουμε εὐθεῖες ε1καὶ ε2 κάθετες στὴν εὐθεία ε.
Ἐπὶ τῆς εὐθείας ε παίρνουμε εὐθύγραμμο τμῆμα ΗΒ1 ἴσο μὲ τὴ μονάδα, ἴσο μὲ τὴ διάμετρο τοῦ ἐγγεγραμμένου κύκλου.
Κατασκευάζουμε εὐθεία ποὺ ὁρίζεται ἀπὸ τὰ σημεῖα Η καὶ Β, ἡ ὁποία τέμνει τὴν εὐθεία ε2στὸ σημεῖο Ζ1.
Ἀπὸ τὸ σημεῖο Β φέρνουμε εὐθεία κάθετη στὸ ΗΖ1 ἡ ὁποία τέμνει τὴν εὐθεία ε2 στὸ σημεῖο Κ1.
Ἀποδεικνύεται (ἐδῶ) πώς ![]()
Ὑπενθυμίζεται πὼς ![]()
Εἴδαμε λοιπόν, μὲ ποιὸν ἄμεσο, ἁπλὸ καὶ ἐμφατικὸ τρόπο, ὁ συγκεκριμένος μηχανισμὸς μᾶς ἔδωσε τὸ εὐθύγραμμο τμῆμα Κ1Γ1 τὸ ὁποῖο ἰσοῦται μὲ τὸν βηματισμό, (τὸν λόγο) τῆς μουσικῆς μας κλίμακας, φανερώνοντας ἔτσι τὴν στενὴ σχέση τοῦ μηχανισμοῦ μὲ τὴ μουσική. Δὲν σταματάει ὅμως ἐδῶ. Θὰ δοῦμε πὼς θὰ μᾶς δώσει καὶ ὅλη τὴ Θεμελιώδη μουσικὴ κλίμακα. Πιὸ πρὶν ὅμως, ἂς θυμηθοῦμε τὴν ἐμφάνιση τῆς 1ης κατὰ φ ἁρμονικῆς συχνότητας καὶ τὴν ἀντίστοιχη ταλάντωση.
Χρυσὴ ἔλλειψη
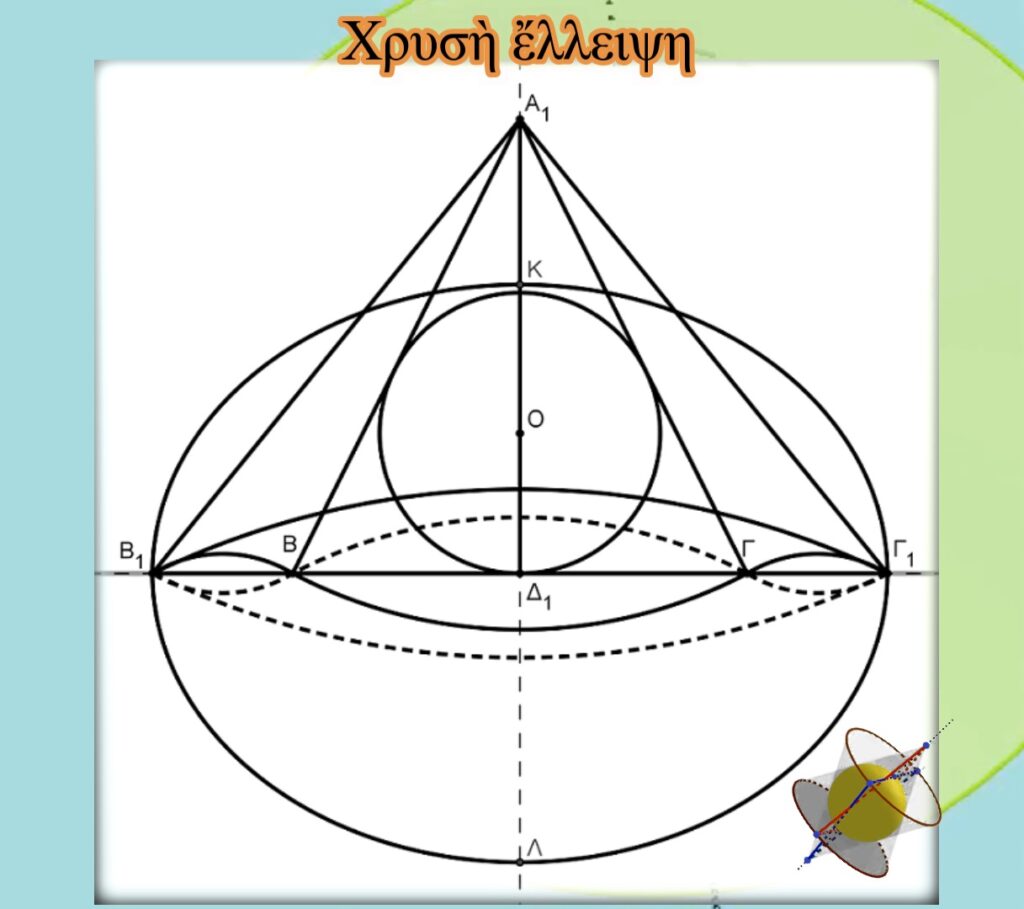
Ἀπὸ κατασκευὴ ἔχουμε ΒΒ1=ΓΓ1. Μποροῦμε νὰ δεχθοῦμε τὴν ὕπαρξη ἔλλειψης μὲ ἑστίες τὰ σημεῖα Β καὶ Γ, μὲ μεγάλο ἄξονα τὸ εὐθύγραμμο τμῆμα Β1Γ1 καὶ μὲ μικρὸ ἄξονα τὸ εὐθύγραμμο τμῆμα ΚΛ. Ὁ μικρὸς της ἄξονας θὰ ἰσοῦται μὲ τὸ διπλάσιο τῆς τετραγωνικῆς ρίζας τοῦ γινομένου τῶν εὐθυγράμμων τμημάτων Β1Β καὶ ΒΓ1. Θὰ εἶναι δηλαδὴ
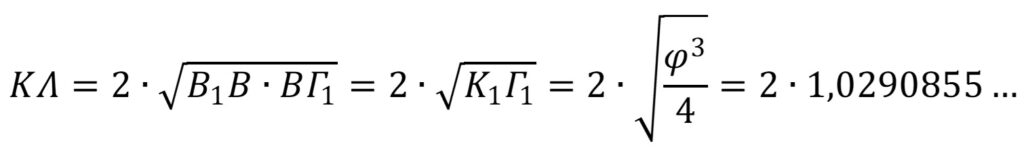
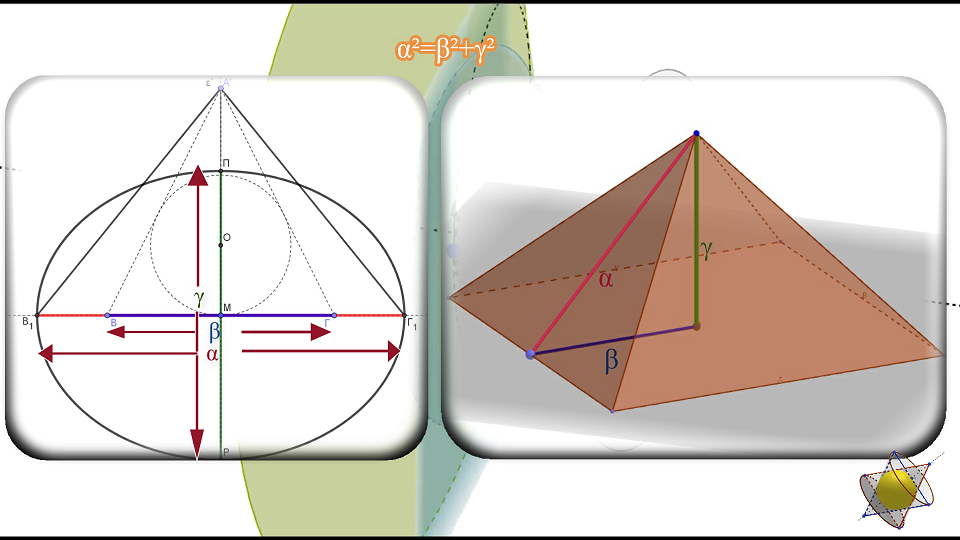
Οἱ ἀναλογίες μεγάλου ἄξονα Β1Γ1, ἑστιακῆς ἀπόστασης ΒΓ καὶ μικροῦ ἄξονα ΚΛ τῆς χρυσῆς ἔλλειψης ποὺ προκύπτει, εἶναι φ:1:√φ. Τὶς ἴδιες ὅμως ἀναλογίες συναντοῦμε καὶ στὸ μεγαλύτερο καὶ σημαντικώτερο μεγαλιθικὸ μνημεῖο, τὴν μεγάλη πυραμίδα τοῦ Χέοπος. Ἡ διαπίστωση αὐτὴ εἶναι ἰδιαίτερα σημαντική, γιατὶ καταρχὴν μᾶς δηλώνει τὴ μεταξὺ τους σχέση, ταυτόχρονα ὅμως μᾶς ὑποδεικνύει καὶ τὸν τρόπο ποὺ θὰ μπορέσουμε νὰ ξεκλειδώσουμε τὰ σπουδαῖα μυστικὰ ποὺ κρύβει ἡ συγκεκριμένη κατασκευή. Θὰ τὰ δοῦμε στὴ συνέχεια.
Ἐὰν τώρα θεωρήσουμε τὸ εὐθύγραμμο τμῆμα Β1Γ1 χορδὴ ποὺ πάλλεται καὶ τὰ σημεῖα Β καὶ Γ σημεῖα ὅπου σχηματίζονται δεσμοί, τότε ἔχουμε τὶς προϋποθέσεις σχηματισμοῦ τῆς ἰδιαίτερης κατὰ φ ἁρμονικῆς ταλάντωσης.
Τὰ κατὰ φ ἐλλειπτικὰ ἁρμονικὰ κύματα όμως, ὅσο σημαντικὰ καὶ ἂν φαίνεται ὅτι εἶναι, ἐμφανίστηκαν ἕως τώρα μόνο ἐπὶ χάρτου. Γιὰ νὰ μπορέσουμε νὰ τὰ ἀποδεχθοῦμε θὰ πρέπει καὶ νὰ ὑφίστανται. Γιὰ αὐτὸ ἂς θυμηθοῦμε τὴν πειραματικὴ ἀπόδειξη τῆς ὕπαρξης στάσιμων ἐλλειπτικῶν κατὰ φ ἁρμονικῶν ταλαντώσεων.

