Τετρακτύς καὶ Θεμελιώδης Μουσικὴ Κλίμακα
Μαθηματικὴ εὔρεση
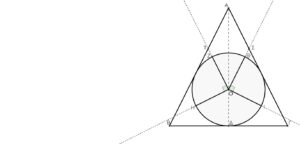
Ἀπό τὸ βιβλίο…

Θὰ ἐργαστοῦμε στὸ εὖρος συχνοτήτων τῆς ὀκτάβας Λὰ (432), δηλαδὴ ἀνάμεσα στὰ 432 Hz καὶ 864 Hz.
1ο βῆμα
Ὅπως γνωρίζουμε, στὴν μουσικὴ καὶ γιὰ τὶς νότες δὲν μᾶς ἐνδιαφέρουν οἱ τιμὲς τῶν συχνοτήτων αὐτούσιες, ἀλλὰ ἡ σύγκριση τους, οἱ ἀναλογίες τους. Θέλουμε νὰ βροῦμε ποιὲς συχνότητες θὰ προκύψουν μὲ λόγο ἴσο μὲ τὸν ἀριθμὸ φ, σὲ σχέση μὲ τὴν ἀρχὴ καὶ τὸ τέλος τῆς κλίμακάς μας, δηλαδὴ σὲ σχέση μὲ τὶς τιμὲς τῶν 432 Hz καὶ 864 Hz . Θὰ θυμηθοῦμε ὅτι: 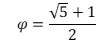
Ἁπλὲς μαθηματικὲς πράξεις μᾶς δίνουν τὶς παρακάτω δύο τιμές.
432,00∙φ=698,9907… καὶ 864/φ=533,9814…
Μὲ μιὰ πρώτη ματιά, δὲν φαίνεται κάτι τὸ ἰδιαίτερο. Πέρα τοῦ ὅτι σὰν συχνότητες ἔχουν τιμὲς ποὺ πλησιάζουν νὰ γίνουν ἀκέραιες, δὲν ταυτίζονται ἀλλὰ οὔτε καὶ δείχνουν κατ’ ἀρχὴν νὰ ἔχουν κάποια σχέση μὲ τὶς νότες τῆς κλίμακάς μας. Πὰραὐτά, θὰ τὸ ἐρευνήσουμε.
Στὸν ἄξονα τῶν πραγματικῶν ἀριθμῶν, τοποθετοῦμε τὶς συχνότητες ποὺ βρήκαμε, σὰν νὰ πρόκειται νὰ εἶναι ἀριθμοί.
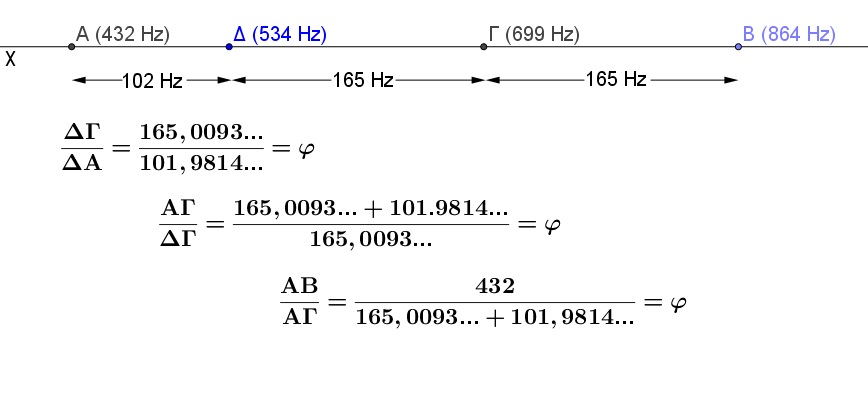
Ὑπολογίζουμε τὶς διαδοχικὲς ἀποστάσεις μεταξὺ συνεχόμενων συχνοτήτων, δηλαδὴ τὶς διαστάσεις τῶν εὐθυγράμμων τμημάτων ποὺ προκύπτουν. Τὸ σημεῖο Δ ποὺ προέκυψε μὲ βάση τὴν τιμὴ τοῦ σημείου Β (864 Hz), τέμνει τὸ εὐθύγραμμο τμῆμα ΑΓ σὲ δύο ἐπιμέρους τμήματα, τὸ ΑΔ καὶ τὸ ΔΓ. Ἡ σύγκριση τους μᾶς δίνει τὴν τιμὴ φ, δηλαδὴ τὸ σημεῖο Δ εἶναι ἡ Χρυσὴ τομὴ τοῦ ΑΓ εὐθυγράμμου τμήματος. Τὸ εὐθύγραμμο τμῆμα ΑΓ ὅμως δὲν σχετίζεται μὲ τὸ σημεῖο Δ πέρα ἀπὸ τὴ μουσικὴ σχέση διπλάσιας τιμῆς τοῦ σημείου Β ἀπὸ αὐτὴν τοῦ Α.
ΔΓ/ΑΔ=(165,0093…)/(101,9814…)=1,618034…=φ
Ἀναμενόμενο εἶναι πὼς ΑΓ/ΔΓ=(165,0093…+101,9814…)/(165,0093…)=1,618034…=φ
καθὼς καὶ ΑΒ/ΑΓ=432/(165,0093…+101,9814…)=1,618034…=φ
Ἡ ἐμφάνιση τῆς χρυσῆς τομῆς μὲ τρείς διαφορετικούς τρόπους, προέκυψε ἀποκλειστικά καὶ μόνο γιατί χρησιμοποιήσαμε τον βασικό κανόνα της μουσικής που θέλει τὴν ἐμφάνιση τῆς ἴδιας νότας μὲ διπλασιασμό τῆς συχνότητας (Α=432 και Β=864).
Εἶναι βέβαιο λοιπόν ὅτι οἱ τιμὲς δὲν εἶναι τυχαῖες, εἶναι βέβαιο πὼς κινούμαστε στὴ σωστὴ κατεύθυνση.
Ὁ βηματισμὸς τῆς μουσικῆς κλίμακας
Μετὰ τὴ σύγκριση τῶν ἀποστάσεων (διαστημάτων) μεταξὺ τῶν συχνοτήτων, θὰ συγκρίνουμε καὶ τὶς ἀπόλυτες τιμὲς τους. Διαδοχικὰ ἔχουμε: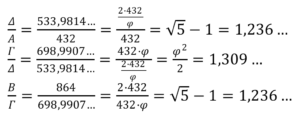
Οἱ λόγοι μᾶς προτρέπουν σὲ ἔλλειψη, ὅπου ἐὰν ἡ ἑστιακὴ της ἀπόσταση εἶναι: 1,309…=φ2/2 , τότε ἡ ἀπόσταση τῆς κάθε ἑστίας ἀπὸ τὴν κοντινότερη ἄκρη τοῦ μεγάλου ἄξονα θὰ εἶναι ἴση μὲ 1,236…=√5-1.
Τὸ πραγματικὰ πολὺ ἐνδιαφέρον ὅμως εἶναι ὁ λόγος τους.
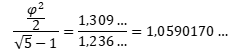
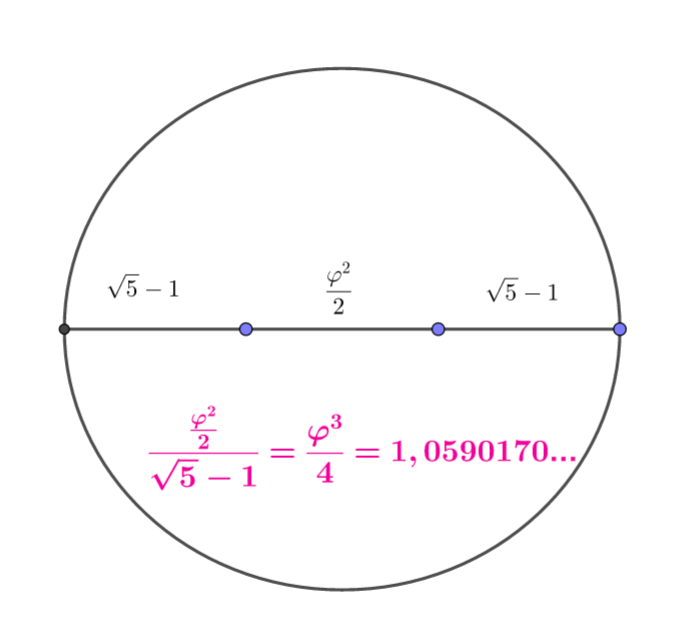
Τὴν τιμὴ μποροῦμε νὰ τὴν μορφοποιήσουμε:
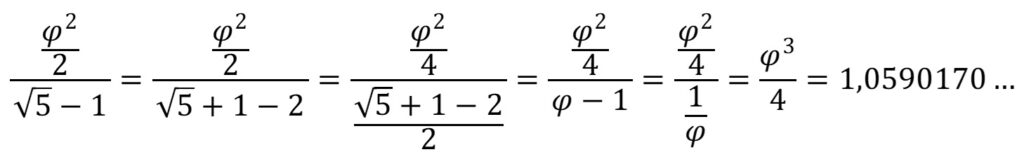
Ἡ τιμὴ πλησιάζει κατὰ πολὺ τὴν τιμὴ![]()
Εἶναι ἡ τιμὴ τοῦ βήματος στὴν ἀποδεκτὴ 12-τονική μουσικὴ μας κλίμακα, ὅταν τὴν δοῦμε σὰν κλίμακα, σὰν σκάλα ποὺ τὴν ἀνεβαίνουμε σκαλὶ σκαλὶ μὲ τὸν ἴδιο βηματισμό. Ἡ ἀπόκλιση εἶναι ἴση μὲ 1,0594631…/1,0590170…=1,00042124… , σαφῶς πολὺ μικρότερη καὶ ἀπὸ τὴν ἀπόκλιση τῆς πυθαγόρειας μουσικῆς κλίμακας, ποὺ τὴν ὑπολογίσαμε στὴν τιμὴ 1,001142…
Ἔτσι, ἔστω καὶ ἔμμεσα, ἀπὸ τὴν πρώτη κιόλας ἐνέργεια μας, ἔχουμε τὴν ἐμφάνιση τῆς τιμῆς, ποὺ θὰ εἶναι καὶ ἡ πρόταση τοῦ ἀριθμοῦ φ γιὰ τὸν βηματισμὸ τῆς μουσικῆς κλίμακας, τὴν ἐμφάνιση τοῦ λόγου 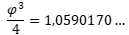
Ἡ ἴδια ἡ συχνότητα ὅμως ἀκόμη δὲν ἐμφανίστηκε.
2ο βῆμα
Ἡ πυθαγόρεια μουσικὴ κλίμακα στηρίζεται στὴν εὕρεση τῆς ἑπόμενης νότας πολλαπλασιάζοντας τὴν συχνότητα τῆς προηγούμενης νότας μὲ τὴν τιμὴ 3/2. Ἀνάλογα θὰ πράξουμε καὶ ἐδῶ. Τὸ γινόμενο 432,00∙φ=698,9907… θὰ τὸ πολλαπλασιάσουμε μὲ τὸν ἀριθμὸ φ, ἐνῶ τὸ πηλίκο 864/φ=533,9814… θὰ τὸ διαιρέσουμε μὲ τὸν ἀριθμὸ φ. Ἔτσι ἔχουμε (432,00∙φ)∙φ=698,9907…∙φ=1130,9906… καὶ γιὰ βρεθοῦμε ἐντὸς ὁρίων τῆς μουσικῆς ὀκτάβας ποὺ κινούμαστε, τὸ ἀποτέλεσμα τὸ διαιροῦμε μὲ τὸν ἀριθμὸ 2. Ὁπότε ἔχουμε:
432∙φ2/2=565,4953…
Ἀντίστοιχα μὲ διαίρεση τῆς συχνότητας τῶν 864 Hz μὲ τὴν τιμὴ φ2 καὶ μετακινώντας τὸ ἀποτέλεσμα ἐντὸς τῶν ὁρίων τῆς ὀκτάβας μας, παίρνουμε:
![]()
Οἱ νέες συχνότητες καὶ πάλι δὲν δείχνουν κάποια ἰδιαίτερη σχέση μὲ τὶς ἰσχύουσες συχνότητες τῆς κλίμακάς μας. Οἱ νέες μας συχνότητες ὅμως, ἔχουν μιὰ πολὺ ἰδιαίτερη σχέση μὲ τὶς δύο προηγούμενες. Συγκρινόμενοι καὶ μάλιστα χιαστί, δηλαδὴ προερχόμενοι ἀπὸ διαφορετικὲς διαδρομές, δίνουν τὴν τιμὴ
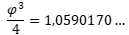
Πράγματι : 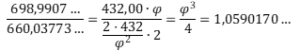
ἀλλὰ καὶ 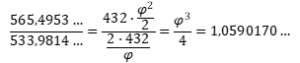
3ο βῆμα
Συνεχίζουμε καὶ τὶς δύο προηγούμενες συχνότητες τὶς πολλαπλασιάζουμε καὶ τὶς διαιροῦμε ἀντίστοιχα μὲ τὸν ἀριθμὸ φ. Τὰ ἀποτελέσματα τὰ φέρνουμε ἐντὸς ὁρίων κλίμακας. Ἔτσι ἔχουμε :

Μὲ βάση τὴν ἰσχύουσα κλίμακα γιὰ νὰ βρεθοῦμε στὴ ἑπόμενη νότα, θὰ πρέπει κάθε φορὰ νὰ πολλαπλασιάζουμε τὴ συχνότητα τῆς νότας ποὺ βρισκόμαστε μὲ τὴν δωδέκατη ρίζα τοῦ 2, ἔτσι ὥστε μετὰ ἀπὸ δώδεκα ἐξελικτικὰ βήματα νὰ βρεθοῦμε στὴν ἴδια μὲ τὴν ἀρχικὴ νότα, ἀλλὰ κατὰ μιὰ ὀκτάβα πιὸ πάνω (διπλάσια συχνότητα). Ὁπότε ἔχουμε:![]()
ἀλλὰ καὶ ![]()
ὅπως ἐπίσης : ΣΟΛ#=815,5074… ἀλλὰ καὶ 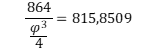
Αὐτὴ εἶναι καὶ ἡ πρόταση τοῦ ἀριθμοῦ φ γιὰ τὴ μουσικὴ κλίμακα. Τὰ σημαντικώτερα συμπεράσματα εἶναι τὰ ἀκόλουθα:
– Ἀπὸ κάθε νότα, ἀπὸ κάθε συχνότητα, μποροῦμε νὰ πᾶμε στὴν ἀμέσως ἑπόμενη, πολλαπλασιάζοντας αὐτὴν μὲ τὴν τιμὴ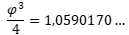
Ἡ ἀπόκλιση ἀπὸ τὴν ἰσχύουσα τιμή, ὅπως εἴδαμε εἶναι ἐλάχιστη (λ=1,00042124…). Εἶναι πολὺ σημαντικὸ ὅτι ἔτσι ἄμεσα προκύπτει τὸ ἑπόμενο βῆμα τῆς μουσικῆς κλίμακας, ὑπάρχει δηλαδὴ ὁ βασικὸς κανόνας τῆς ἀκολουθίας, ὑπάρχει ἡ σκάλα.
– Ὅπως εἴδαμε καὶ στὴν μελέτη τῆς ἀκολουθίας τοῦ ἀριθμοῦ φ καὶ τῆς σχέσης της μὲ τὶς σειρὲς Fibonacci, Lucas καὶ Χ, ἔτσι καὶ ἐδῶ, γιὰ νὰ φτάσουμε στὴν ἑπόμενη νότα, περνᾶμε πρῶτα ἀπὸ δύο ἐνδιάμεσους σταθμοὺς (τριαδικότητα). Οἱ θέσεις αὐτές, ὅπως θὰ δοῦμε καὶ στὴ συνέχεια, εἶναι ἀπολύτως καθορισμένες.
Ἡ πιὸ κοντινὴ νότα στὴν 432,00∙φ=698,9907… συχνότητα, εἶναι ἡ νότα ΦΑ μὲ συχνότητα ἴση μὲ 685,7573…Hz. Ὁ λόγος τῶν δύο συχνοτήτων, ποὺ καθορίζει καὶ τὴ θέση τῆς νέας νότας εἶναι :
698,9907/685,7573=1,0192974…
Ἡ τιμὴ αὐτὴ ὅμως δὲν εἶναι τυχαία, ἰσοῦται μὲ τὴν ∛(1,0590170…)=1,0192974…Δηλαδή ὁ συγκεκριμένος λόγος ἰσοῦται μὲ τὴν τρίτη ρίζα τοῦ βήματος γιὰ τὴν 12-τονική μουσικὴ κλίμακα τοῦ φ.
Ἐδῶ θὰ πρέπει νὰ προσέξουμε γιὰ νὰ κατανοήσουμε τὴν σημαντικώτερη πληροφορία ποὺ μᾶς δίνεται, δηλαδὴ τὸ κλειδὶ λειτουργίας τῆς νέας μας κλίμακας.
Ἔχουμε ὀρθῶς ἀποδεχθεῖ πὼς ἡ 12-τονική μουσικὴ κλίμακα εἶναι ἕνα φυσικὸ ἐξελικτικὸ φαινόμενο ὅπου ἡ κάθε ἑπόμενη νότα ἔχει συχνότητα κατὰ 12√2 φορὲς μεγαλύτερη τῆς προηγούμενης, ἔτσι ὥστε μετὰ ἀπὸ 12 ἐξελικτικὰ βήματα, νὰ πάρουμε τὴν ἴδια μὲ τὴν ἀρχικὴ νότα διπλάσιας συχνότητας. Ὁπότε, μὲ ἀρχικὴ νότα τὴν ΛΑ στὰ 432 Hz, μετὰ ἀπὸ ὀκτὼ ἐξελικτικὰ βήματα προκύπτει ἡ νότα ΦΑ στὰ![]()
Εἶναι δεδομένη συχνότητα, ὅπου στὴν εὕρεση της δὲν ἐμπλέκεται ὁ ἀριθμὸς φ.
Ὁ ἀριθμὸς φ ἐμπλέκεται ὅμως στὴν ἐμφάνιση τῆς πρώτης ἐνδιάμεσης συχνότητας μὲ λόγο φ καὶ τιμὴ 432·φ=698,9907…Hz.
Ὅπως εἴδαμε, ἡ σύγκριση τῶν δύο συχνοτήτων μᾶς δίνει λόγο ἴσο μὲ τὴν τρίτη ρίζα τοῦ φ³/4.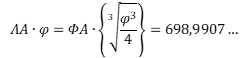
Αὐτὴ ἡ ἀπόλυτη ταύτιση τῶν ἀποτελεσμάτων, ἐπιβάλει νὰ ἀποδεχθοῦμε ὅτι ἡ ὀρθὴ ἀπόδοση τῆς δωδεκατονικής μουσικῆς κλίμακας εἶναι αὐτὴ μὲ τὴν μορφὴ γεωμετρικῆς προόδου μὲ λόγο λ ἴσο μὲ ![]()
Ταυτόχρονα μᾶς προϊδεάζει γιὰ τὴν ἰσχυρὴ σχέση ποὺ ὑπάρχει μεταξὺ τῆς 12-τονικής μουσικῆς κλίμακας καὶ τῆς μουσικῆς κλίμακας τοῦ ἀριθμοῦ φ ποὺ ἀρχίζει νὰ ἀποκαλύπτεται.

