Τετρακτύς καὶ Θεμελιώδης Μουσικὴ Κλίμακα
Θεμελιώδης ὀκτατονικὴ μουσικὴ κλίμακα
Ἀπό τὸ βιβλίο…

Παρατηρώντας τὸν πίνακα τῆς 36-τονικῆς μουσικῆς κλίμακας, μποροῦμε νὰ ποῦμε ὅτι ἔχουμε
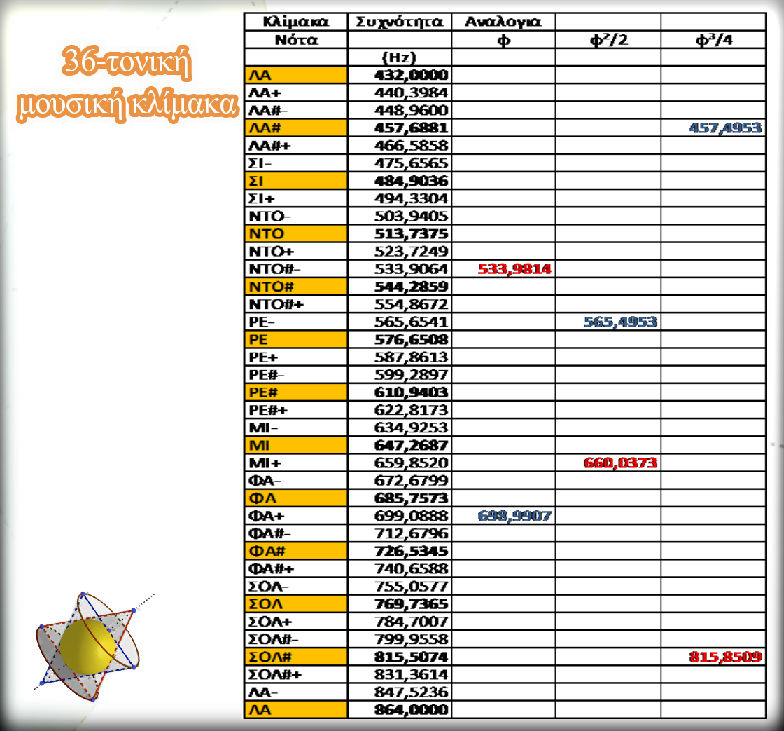
- δύο νότες, τὴν Λα(432) καὶ Λα(864), τὶς ὁποῖες μποροῦμε νὰ θεωρήσουμε σὰν ἀρχικὴ καὶ τελικὴ νότα ὀκτατονικής μουσικῆς κλίμακας,
- ἐπίσης δύο νότες ποὺ προκύπτουν ἀπὸ τὶς ἀρχικές, μὲ λόγους συχνοτήτων τὸν ἀριθμὸ φ, τὴν ΝΤΟ#–(534) καὶ τὴν ΦΑ+(699),
- ἄλλες δύο νότες ποὺ προκύπτουν ἀπὸ τὶς ἀρχικὲς σὰν λόγοι κλασμάτων τοῦ φ2/2, ἡ ΡΕ-(565) καὶ ἡ ΜΙ+(660)
- καὶ τέλος, δύο νότες ποὺ προκύπτουν ἀπὸ τὶς ἀρχικές, μὲ λόγο συχνοτήτων ἴσο μὲ κλάσμα τοῦ φ3/4, τὶς νότες ΛΑ#(458) καὶ ΣΟΛ#(816).
Στὸ σύνολό τους οἱ νότες εἶναι ὀκτώ. Τὶς τοποθετοῦμε στὴ σειρά.
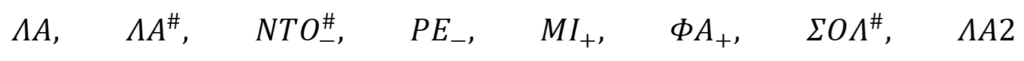
Θὰ μποροῦσε αὐτὴ ἡ ἀκολουθία μουσικῶν φθόγγων νὰ ἀποτελέσει μουσικὴ κλίμακα καὶ ἐὰν ναί, μὲ ποιὰ κριτήρια;
Τὰ κριτήρια τὰ ὁποία ἔχουμε, εἶναι αὐτὰ ποὺ προέκυψαν ἀπὸ τὶς συγγενικὲς σχέσεις τῶν ἁρμονικῶν συχνοτήτων μὲ τὴν θεμελιώδη συχνότητα, ὅπως αὐτὲς περιεγράφησαν μὲ τὰ στάσιμα κύματα. Μπορεῖ νὰ παρουσιάζονται κάποια κενὰ ἢ ἀτέλειες ἢ δεδομένα ποὺ ἀκόμα δὲν μπόρεσαν νὰ ἑρμηνευτοῦν, ἐντούτοις καὶ μόνο ἀπὸ τὸ ἀποτέλεσμα, τὰ κριτήρια αὐτὰ τὰ ἀποδεχόμαστε. Θὰ τὰ θυμηθοῦμε καὶ μάλιστα μὲ σειρὰ συγγενικῆς ἰσχύος.
Ἡ 2η ἁρμονικὴ συχνότητα. Συχνότητα διπλάσια τῆς θεμελιώδους καὶ μὲ ἴδια ἠχητικὴ αἴσθηση.
Ἡ 3η ἁρμονικὴ συχνότητα. Εἶναι συχνότητα κατὰ 3/2 ὑψηλότερη τῆς θεμελιώδους. Ἀπέχει ἀπὸ τὴν θεμελιώδη συχνότητα ἑπτὰ (7) ἡμιτόνια. Ἔτσι, ἐὰν ἡ νότα μας εἶναι ἡ ΛΑ, τότε ἡ 3η ἁρμονικὴ θὰ εἶναι ἡ νότα ΜΙ.
Ἡ 5η ἁρμονικὴ συχνότητα. Εἶναι κατὰ 5/4 ὑψηλότερη τῆς θεμελιώδους καὶ ἀπέχει ἀπὸ αὐτὴν τέσσερα (4) ἡμιτόνια. Ἔτσι, ἡ 5η ἁρμονικὴ τῆς ΛΑ εἶναι ἡ νότα ΝΤΟ#.
Ἡ 7η ἁρμονικὴ θὰ μᾶς ἔδινε συχνότητα κατὰ 7/4 ὑψηλότερη τῆς θεμελιώδους, ἀλλὰ δὲν συμπεριλαμβάνεται, μὲ τὰ σημερινὰ ἰσχύοντα δεδομένα, στὶς ἀποδεκτὲς συχνότητες. Ὁ λόγος ποὺ δὲν συμπεριλήφθηκε συνδέεται μὲ τὴν ὕπαρξη τῆς 36-τονικής κλίμακας τὴν ὁποία καὶ ἐπιβεβαιώνει.
Ἡ 9η ἁρμονική, μὲ συχνότητα κατὰ 9/8 ὑψηλότερη τῆς θεμελιώδους καὶ ἀπόσταση δύο (2) ἡμιτονίων ἀπὸ αὐτήν.
Ὁ ἰσχύων κανόνας τῆς τονικότητας ποὺ μᾶς τὸν ὑπέδειξε καὶ ἡ πυθαγόρεια μουσικὴ κλίμακα, ἀλλὰ καὶ ἡ Τετρακτύς.
Θὰ θέσουμε ἀκόμη ἕνα κριτήριο, αὐτὸ τῆς σχέσης δύο συχνοτήτων μὲ λόγο φ. Τὸ εἴδαμε σὲ θεωρητικὸ ἐπίπεδο, θὰ τὸ ἀποδείξουμε καὶ πειραματικὰ ἀργότερα.
Τέλος, ἀποκλίσεις συχνοτήτων τῆς νέας κλίμακας μας, μικρότερες τοῦ ἑνὸς μικροημιτονίου, ἀπὸ αὐτὲς τῶν παραπάνω κριτηρίων, θὰ τὶς ἀποδεχόμαστε.
Ἀναλυτικά, οἱ συγγενικὲς σχέσεις μεταξὺ τῶν νοτῶν τῆς νέας μας μουσικῆς κλίμακας περιγράφονται στὸ βιβλίο «Ἡ χρυσὴ τομὴ στὴ μουσικὴ». Συγκεντρωτικὰ φαίνονται στὸν ἑπόμενο πίνακα.
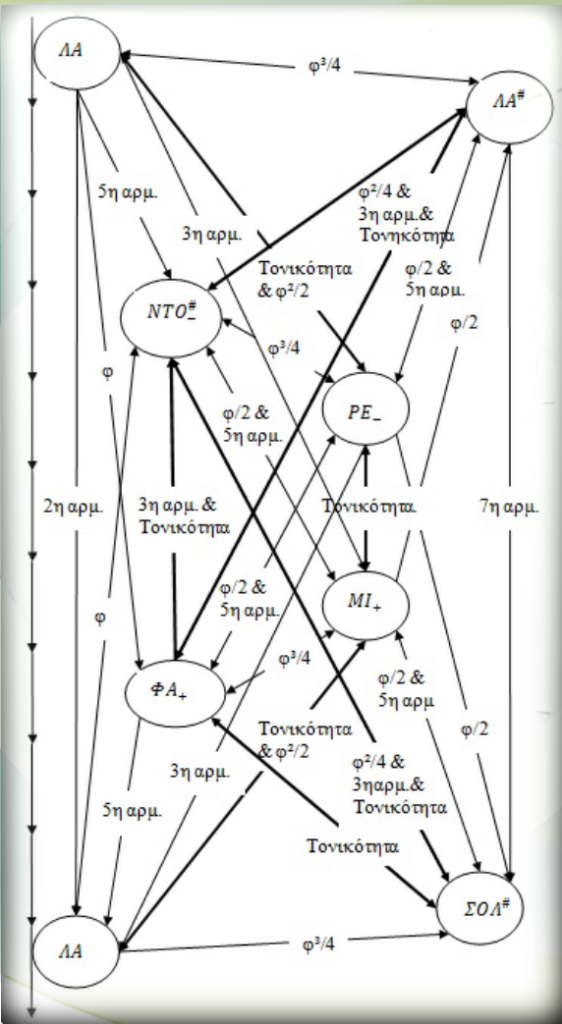
Ἡ προαναφερθείσα μουσικὴ κλίμακα εἶναι ἰδιαίτερα σημαντική, γιατὶ εἶναι ἡ κλίμακα
- μὲ τὴν πληρέστερη κάλυψη σχέσεων συγγενείας μεταξὺ τῶν μουσικῶν φθόγγων ποὺ τὴν ἀπαρτίζουν.
- μὲ ἐφαρμογὲς της ξεπερνοῦν τὰ ὅρια τῆς μουσικῆς, ὅπως τὰ κατανοοῦμε σήμερα.
- ποὺ γεφυρώνει τὶς προϋπάρχουσες.
Ἐπειδὴ μάλιστα προέκυψε ἄμεσα καὶ ἁπλούστατα, μποροῦμε νὰ τὴν θεωρήσουμε σὰν τὴν Θεμελιώδη Μουσικὴ Κλίμακα. Στὴ συνέχεια θὰ δοῦμε μὲ ποιὸ τρόπο, γεωμετρικὰ μᾶς δίνεται ἡ συγκεκριμένη μουσικὴ κλίμακα, ποιὰ συμπεράσματα θὰ προκύψουν καὶ ποιὲς ἐνδείξεις θὰ ἐμφανιστοῦν, ποὺ θὰ μᾶς ἐπιτρέψουν καὶ πειραματικὰ νὰ ἀποδείξουμε καὶ νὰ τεκμηριώσουμε τὴν ὀρθότητα τῆς μεγάλης αὐτῆς ἀνακάλυψης.

