Τετρακτύς καὶ Θεμελιώδης Μουσικὴ Κλίμακα
Εἰσαγωγή
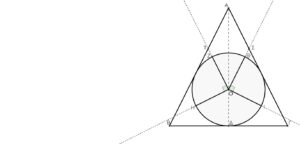
Ἀπό τὸ βιβλίο…
Ἕως τώρα εἴδαμε τὴν Τετρακτύν, νὰ ἐπιβεβαιώνει τὴν ὕπαρξη τῆς πυθαγόρειας μουσικῆς κλίμακας.
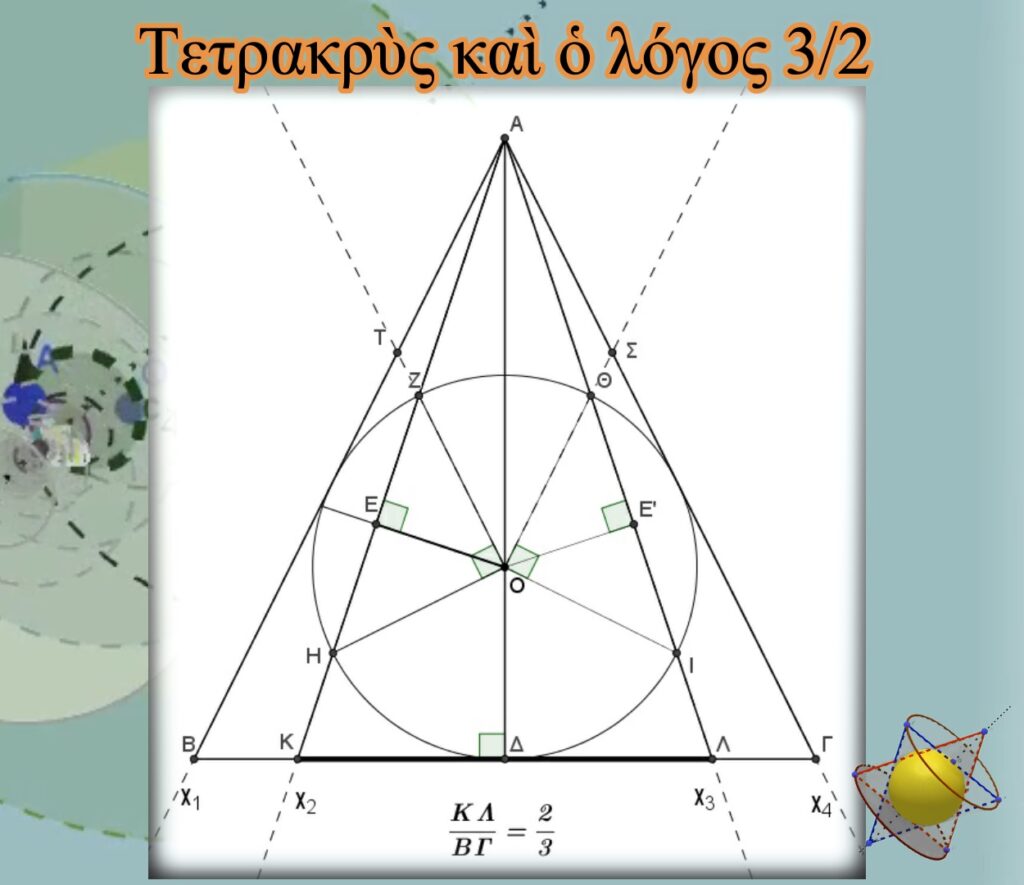
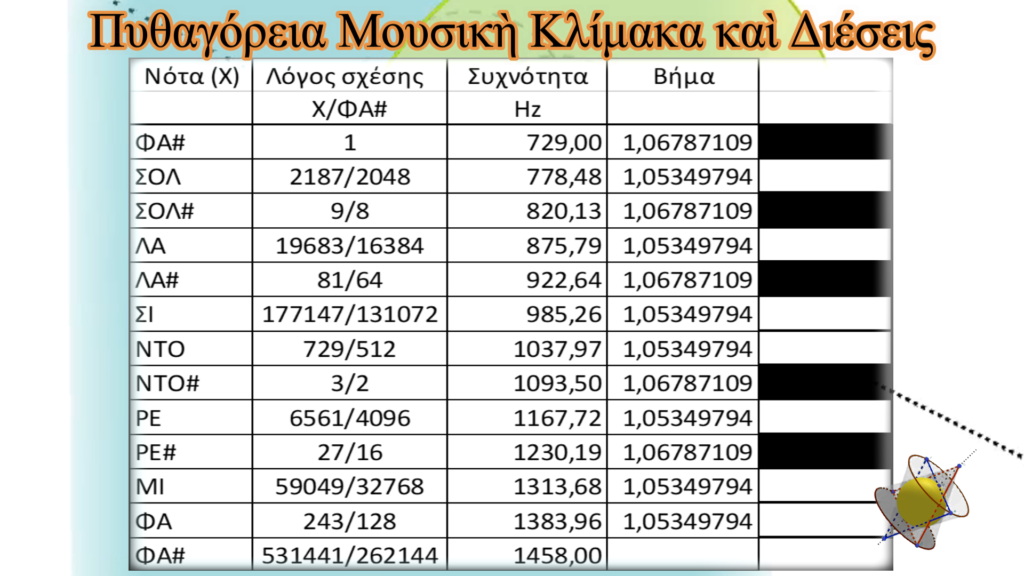
Τὴν εἴδαμε ἐπίσης νὰ ἐπιβεβαιώνει καὶ τὴν ὀρθότητα τῆς κλασσικῆς μουσικῆς κλίμακας ποὺ στηρίζεται στὰ στάσιμα κύματα.
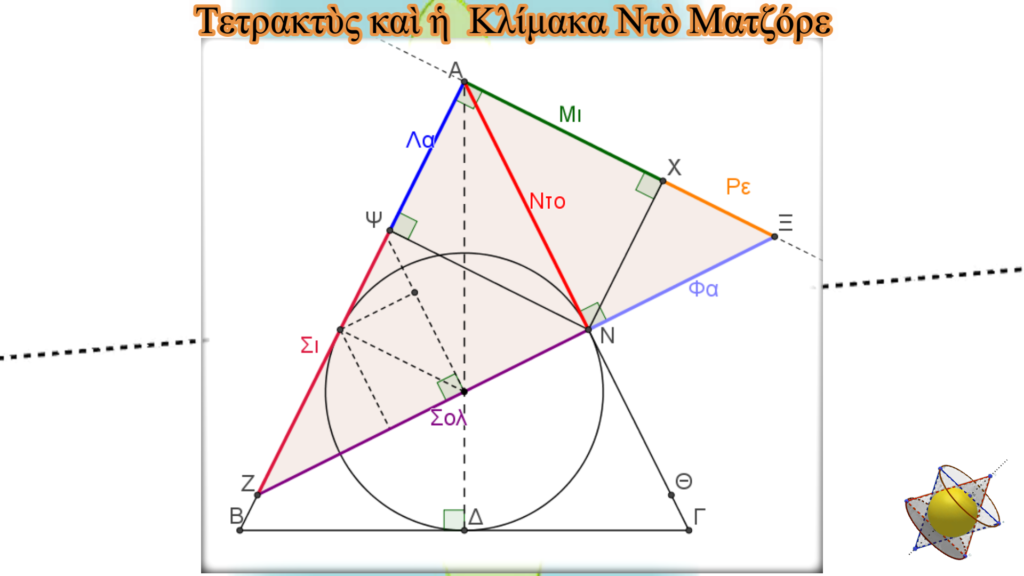
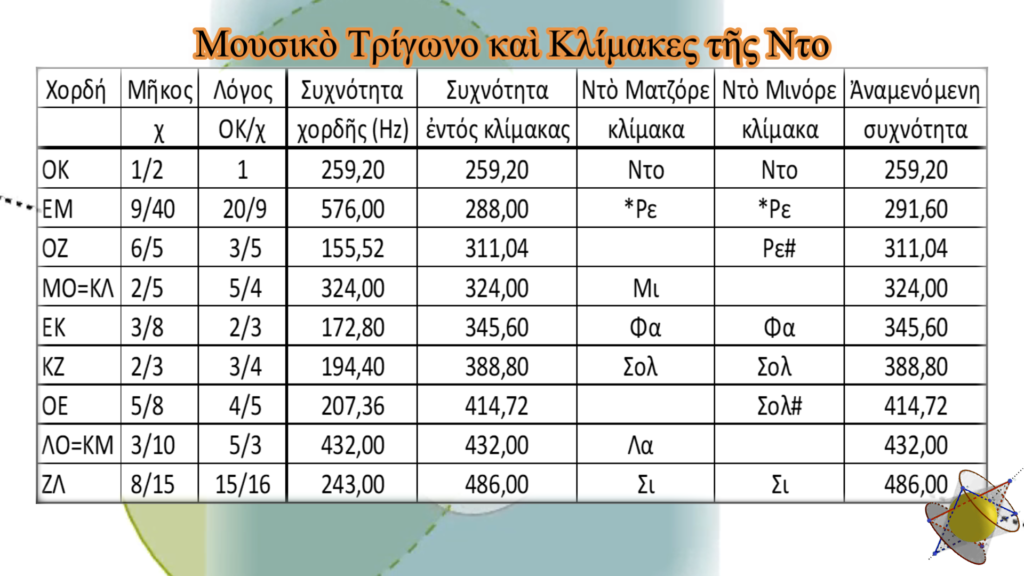
Τὸ βασικὸ ὅμως χαρακτηριστικὸ αὐτῆς, ὅταν θὰ τὴν δοῦμε σὰν Χρυσὸ Τρίγωνο εἶναι ἡ ἐμφάνιση τοῦ ἀριθμοῦ φ.
Τὸ ἐρώτημα ποὺ γεννᾶται εἶναι ἁπλό. Μπορεῖ νὰ ὑπάρχει μουσικὴ κλίμακα ποὺ νὰ στηρίζεται στὴν ἀναλογία τῆς χρυσῆς τομῆς;
Θὰ κάνουμε ὅτι πιὸ ἁπλὸ θὰ μπορούσαμε νὰ φανταστοῦμε. Θὰ βροῦμε τὴ Χρυσὴ Τομὴ τῆς μουσικῆς. Αὐτὸ θὰ τὸ πράξουμε καὶ ἀριθμητικά, μὲ τὶς συχνότητες καὶ γεωμετρικά, μὲ τὶς χορδές. Πιὸ πρὶν ὅμως, ἂς πάρουμε τὴν συγκατάθεση τῆς Τετρακτύος.
Ἀπὸ κατασκευῆς, στὴν Τετρακτύν ἔχουμε τὸν λόγο τῆς βάσης τοῦ τριγώνου πρὸς τὴν διάμετρο τοῦ ἐγγεγραμμένου κύκλου της, ἴσο μὲ τὸν ἀριθμὸ φ. ΒΓ/2ΟΔ=φ.
Ἔτσι, ἐὰν τὸ εὐθύγραμμο τμῆμα ΒΓ ἦταν χορδὴ ποὺ θὰ μᾶς ἔδινε γιὰ παράδειγμα τὴ νότα Λὰ στὰ 432 Hz, τότε ἡ ὁποιαδήποτε διάμετρος τοῦ ἐγγεγραμμένου κύκλου θὰ ἔδινε παλλόμενη τὴ συχνότητα τῶν 432/φ=698,99Hz, δηλαδὴ ἡ μεταξύ τους συχνότητες θὰ εἶχαν λόγο ἴσο μὲ τὴν τιμὴ τῆς χρυσῆς τομῆς.
Ἔχουμε λοιπόν ἐξαρχῆς τὰ ἀπαραίτητα διαπιστευτήρια.
Πάραυτα, θὰ τὸ ἐρευνήσουμε λίγο παραπάνω.
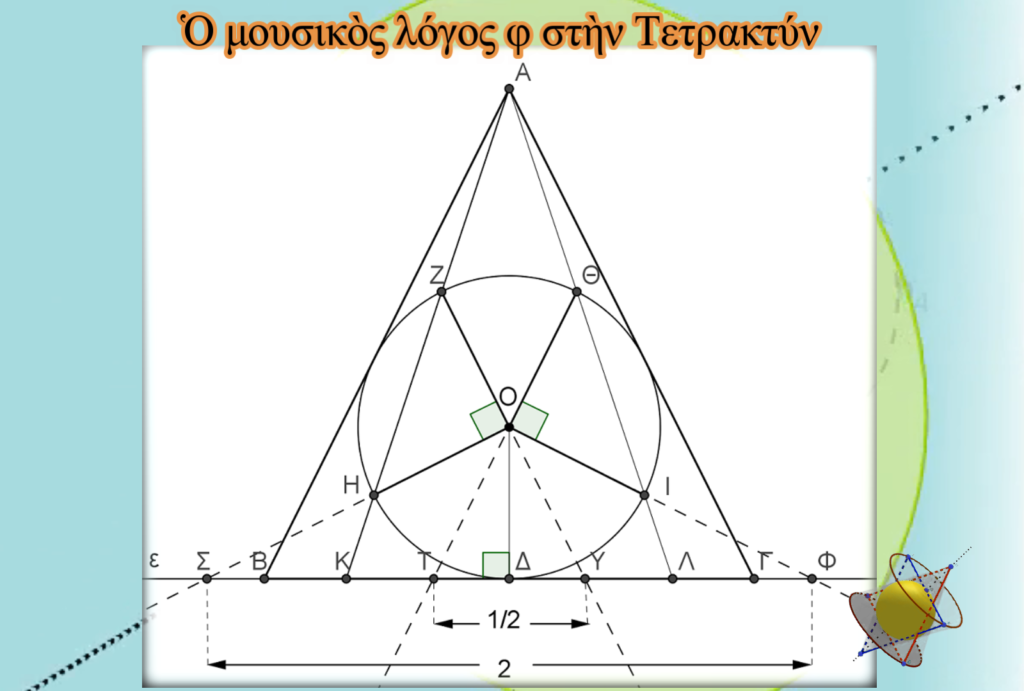
Ὅπως εἴδαμε στὴν Τετρακτύν ἐμφανίζονται οἱ ἰδιαίτερες ἀκτίνες ΟΗ,ΟΖ,ΟΘ καὶ ΟΙ. Εἶναι σὲ ἀριθμὸ τέσσερις καὶ ἐνδεχομένως νὰ εὐθύνονται καὶ γιὰ τὸ ὄνομα Τετρακτύς. Οἱ προεκτάσεις αὐτῶν τέμνουν τὴν εὐθεία ποὺ ὁρίζεται ἀπὸ τὴ βάση τοῦ τριγώνου ΒΓ στὰ σημεῖα Σ,Τ,Υ καὶ Φ ἀντίστοιχα. Ἔτσι, ἐμφανίζεται ἕνα νέο Χρυσὸ τρίγωνο τὸ ΟΤΥ, ποὺ μὲ περιστροφὴ γύρω ἀπὸ τὸν ἄξονα τοῦ δίνει τὸν μουσικὸ κῶνο 1,
ἀλλὰ καὶ τὸ ΟΣΦ τρίγωνο ποὺ μὲ περιστροφὴ μᾶς δίνει τὸν μουσικὸ κῶνο 2.
Ἑπομένως, γιὰ τὸ τρίγωνο ΟΤΥ ἰσχύει: ΤΥ=ΟΔ=1/2 (ἀκτίνα μοναδιαίου κύκλου).
Θεωροῦμε ὅτι ἔχουμε χορδὴ μήκους ΒΓ ποὺ ὅταν πάλλεται παράγει ἦχο συχνότητας 432Hz. Τότε, τὸ τμῆμα τῆς χορδῆς ΤΥ θὰ παράγει ἦχο συχνότητας ΒΓ/ΤΥ∙432=2φ∙432 Ηz=1397,98Ηz, κατὰ μιὰ ὀκτάβα δηλαδὴ ὑψηλότερη τῆς συχνότητας τῶν 698,99Ηz (ἐμφάνιση ἀναλογίας φ 698,99/432,00=φ).
Γιὰ τὸ ΣΦ εὐθύγραμμο τμῆμα, ὅπως εἴδαμε θὰ ἰσχύει: ΣΦ=2ΟΤ=4ΟΔ=4·1/2=2 καὶ ἔτσι ΣΦ/ΒΓ=2/φ=1,236068… Ἡ συχνότητα ποὺ θὰ παράγεται θὰ εἶναι: φ/2∙432=349,49 Hz, δηλαδὴ κατὰ μία ὀκτάβα χαμηλότερη τῆς συχνότητας τῶν 698,99 Hz=432·φ Hz.
Ἔχουμε ἔτσι καὶ τὶς τέσσερις ἀκτίνες τῆς Τετρακτύος νὰ ὑποστηρίζουν τὴν δημιουργία εὐθυγράμμων τμημάτων μὲ μουσικὲς ἀναλογίες τοῦ ἀριθμοῦ φ καὶ παράλληλα νὰ ἐπιβεβαιώνουν τὴν ὀρθότητα τῆς ἀρχικῆς ἐπιλογῆς τους εἰδικά, ἀλλὰ καὶ τῆς ταύτισης τῆς Τετρακτύος μὲ τὸ Χρυσὸ Τρίγωνο γενικώτερα. Τὸ ὅτι τὰ εὐθύγραμμα τμήματα ΣΦ, ΒΓ καὶ ΤΥ εἶναι συνευθειακά, ἔχει τὴ σημασία του ὡς πρὸς τὸν χῶρο ἐφαρμογῆς τῆς ἀναμενόμενης μουσικῆς κλίμακας μέσα στὸ Σύμπαν. Αὐτὸ ὅμως θὰ τὸ δοῦμε στὸ 4ο μέρος. Στὴ συνέχεια, ἔχοντας καὶ τὴν συγκατάθεση τῆς Τετρακτύος, ἂς προχωρήσουμε βρίσκοντας τὸν μαθηματικὸ τρόπο εὕρεσης τῆς πρωτοεμφανιζόμενης, τοὐλάχιστον γιὰ τὰ νεώτερα χρόνια τῆς ἀνθρώπινης Ἱστορίας, μουσικῆς κλίμακας.
