Τετρακτύς καὶ Θεμελιώδης Μουσικὴ Κλίμακα
36-τονικὴ μουσικὴ κλίμακα - Μικροημιτόνια
Ἀπό τὸ βιβλίο…

Στὴν προηγούμενη σελίδα παρατηρήσαμε πὼς γιὰ νὰ βρεθοῦμε στὴν ἀμέσως ἑπόμενη νότα, θὰ πρέπει πρώτα νὰ περάσουμε ἀπὸ δύο ἐνδιάμεσες. Ἑπομένως, γιὰ τὶς 12 κύριες νότες ποὺ ὑπάρχουν, θὰ ἔχουμε καὶ 24 ἐνδιάμεσες, ἀνεβάζοντας τὸν συνολικό ἀριθμὸ σὲ 36 νότες. Θὰ μπορούσαμε δηλαδὴ νὰ μιλήσουμε γιὰ μία 36-τονική μουσικὴ κλίμακα.
Αὐτήν, ἐὰν θέλουμε νὰ τὴ δημιουργήσουμε ὅπως δημιουργήσαμε καὶ τὴν 12-τονική μουσικὴ κλίμακα, θὰ πρέπει κάθε φορὰ, τὴ συχνότητα ἡ ὁποία προκύπτει νὰ τὴν πολλαπλασιάζουμε μὲ τὴ τιμὴ ³⁶√2, ἔτσι ὥστε μετὰ ἀπὸ 36 βήματα αὐτὴν τὴν φορά, νὰ πάρουμε τὴν ἰδία μὲ τὴν ἀρχικὴ νότα, διπλάσιας συχνότητας. Τὰ ἀποτέλεσμα τὰ βλέπουμε στὸν πίνακα ποὺ ἀκολουθεῖ.
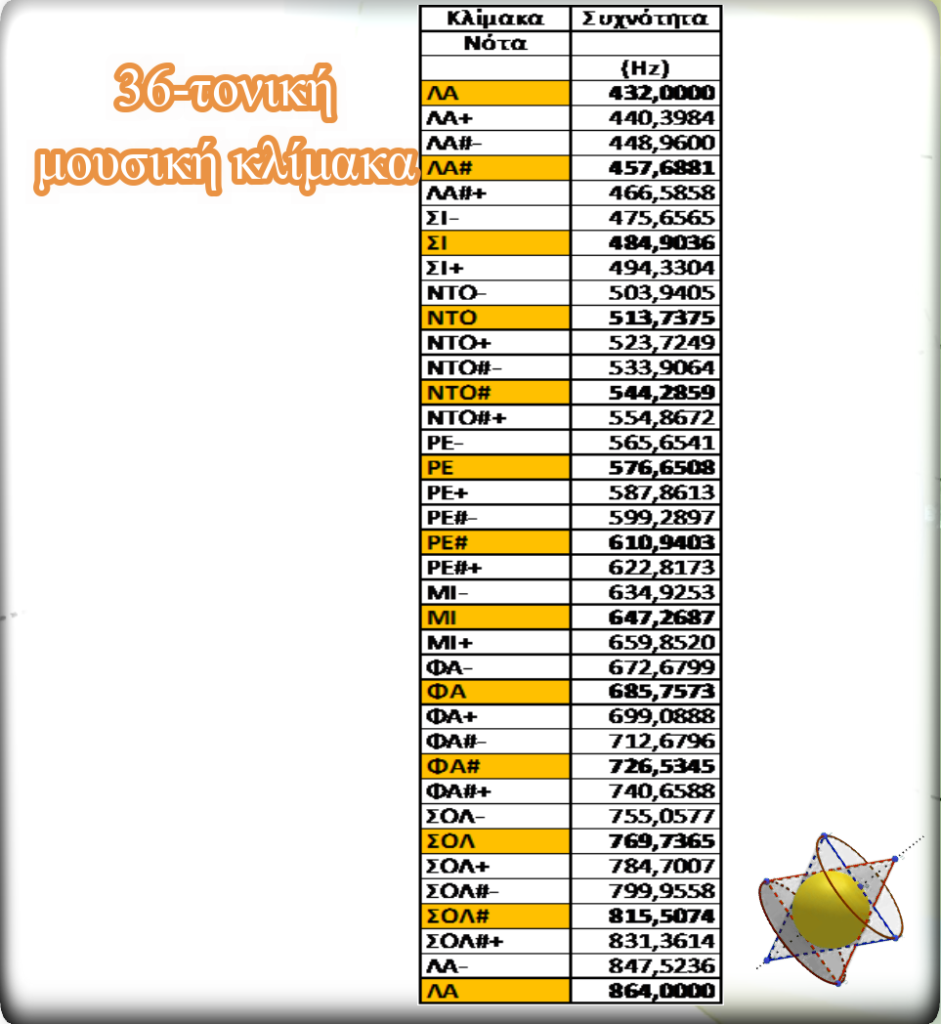
Τὸν λόγο συχνοτήτων μεταξὺ δύο διαδοχικῶν νοτῶν τῆς νέας μας κλίμακας, θὰ τὸν ὀνομάσουμε μικροημιτόνιο.
Εἴδαμε λοιπόν, ὅτι ὁ ἀριθμὸς φ μᾶς πρότεινε τὴν παρουσία δύο ἐνδιάμεσων συχνοτήτων μεταξὺ δύο συνεχόμενων νοτῶν καὶ μάλιστα, μὲ πολὺ συγκεκριμένο καὶ ἀπόλυτο τρόπο, μιὰ νότα κατὰ τὴν τρίτη ρίζα τοῦ φ³/4 φορὲς μεγαλύτερη τῆς κύριας νότας καὶ μία νότα κατὰ τὴν τρίτη ρίζα τοῦ φ³/4 φορὲς μικρότερη. Αὐτές, μὲ ἐλάχιστη ἀπόκλιση ταυτίζονται μὲ τὶς νότες τὴν 36-τονικής κλίμακας. Γενικώτερα, οἱ νέες αὐτὲς νότες, παρόλο ποὺ φαίνεται νὰ εἶναι δευτερεύουσες καὶ προπαρασκευαστικές, εἶναι ἀπόλυτα καθορισμένες καὶ θὰ μποροῦσαν νὰ παίξουν σημαντικὸ ρόλο καὶ στὴ μουσικὴ ἀλλὰ πιθανὸν καὶ σὲ ἐφαρμογὲς ἰδιοσυχνοτήτων καὶ συντονισμῶν μὲ ἠχητικὰ κύματα καὶ ὄχι μόνο. Ἔτσι, σὲ ἰσχυρὰ κβαντισμένες ἐφαρμογὲς (μουσικές καὶ μή), ἡ ὅποια συχνότητα, θὰ πρέπει νὰ ἐπιλέξει καὶ νὰ προσαρμοστεῖ στὴν κοντινότερη ἀπὸ τὶς βασικὲς θέσεις – νότες (κύριος συντονισμός). Σὲ πιὸ ἤπιες ἐφαρμογές, ἡ προσαρμογὴ μπορεῖ νὰ γίνει καὶ μὲ ἐπιλογὴ κοντινότερης βασικῆς ἢ δευτερεύουσας κβαντισμένης θέσης – νότας (δευτερεῦον συντονισμός). Αὐτό, γιὰ τὴ μουσική, θὰ τὸ δοῦμε στὴν πράξη.
Τὶς νέες νότες θὰ τὶς βαπτίσουμε. Οἱ νότες ποὺ θὰ ἔχουν κατὰ ἕνα μικροημιτόνιο χαμηλότερη συχνότητα ἀπὸ τὴν βασική, θὰ χαρακτηρίζονται ἐπιπλέον μὲ τὸ σύμβολο (-) μετὰ τὴν ὀνομασία τῆς νότας, π.χ. ΛΑ#– . Ἀντίστοιχα, οἱ νότες μὲ κατὰ ἕνα μικροημιτόνιο ὑψηλότερη συχνότητα τῆς βασικῆς, θὰ παίρνουν τὸ σύμβολο (+).
Μὲ βάση τὰ προηγούμενα, στὸν ἴδιο πίνακα, προσθέτουμε τρεῖς ἐπιπλέον στῆλες, ὅπου φαίνονται οἱ τιμές, ὅπως προέκυψαν μὲ τὸν προαναφερόμενο μαθηματικὸ μηχανισμὸ καὶ γιὰ ἀναλογίες σὲ σχέση μὲ τοὺς ἀριθμοὺς φ,φ² καὶ φ³ ἀντίστοιχα.
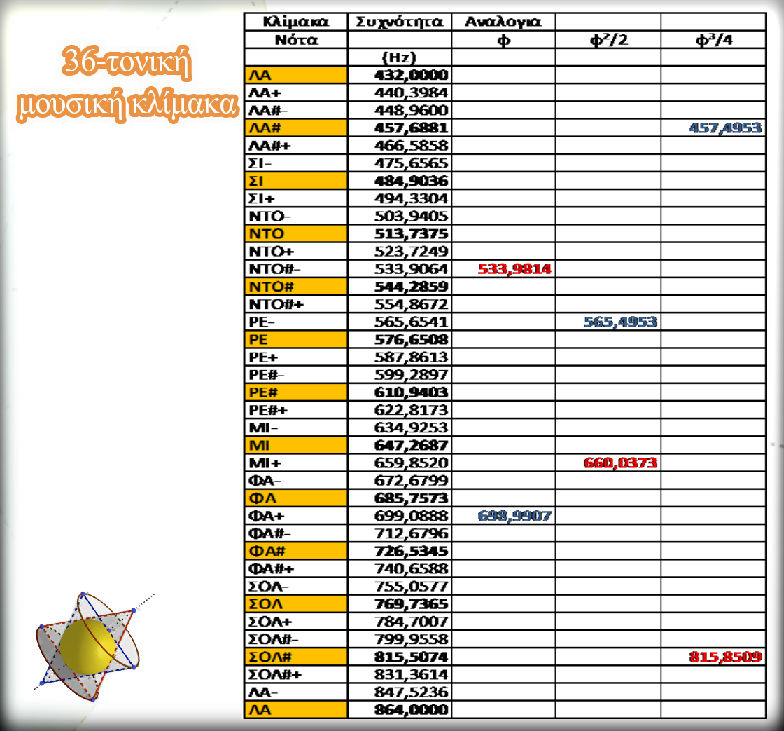
Οἱ συχνότητες 432 Hz καὶ 440 Hz
Ἐπίσης, γιὰ πρώτη φορὰ παρατηροῦμε νὰ ἐμφανίζονται, ταυτόχρονα στὸν ἴδιο πίνακα καὶ μὲ λόγο συχνοτήτων ἴσο μὲ ἕνα μικροημιτόνιο, οἱ συχνότητες 432Hz καὶ 440Hz, δηλαδὴ ἡ συχνότητα ἀναφορὰς ποὺ ἴσχυε καὶ αὐτὴ ποὺ ἐπιβλήθηκε στὶς μέρες μας. Ταυτόχρονα, ἐμφανίζεται καὶ ἡ σχέση ποὺ τὶς ἑνώνει, ὁ μεταξὺ τοὺς λόγος δηλαδή, λόγος τοῦ ἑνὸς μικροημιτονίου.
Ἡ 7η ἁρμονική
Ὅταν μελετήσαμε τὶς συχνότητες καὶ τὰ στάσιμα κύματα, πρὸς μεγάλη ἔκπληξη καὶ ἀπογοήτευση εἴδαμε ὅτι, στὴν δωδεκατονική κλίμακα δὲν συμμετέχει ἡ 7η ἁρμονικὴ συχνότητα, σὲ ἀντίθεση μὲ τὴν λιγότερο ἰσχυρὴ 9η ἁρμονικὴ ποὺ συμμετέχει. Ἂς δοῦμε ποιὰ θὰ ἦταν αὐτὴ γιὰ τὴν νότα ΛΑ(432). Ἔχουμε 432∙7/4=756 Hz. Ἔτσι, ἐνῶ θὰ ἔπρεπε ἡ 7η ἁρμονικὴ γιὰ τὴν ΛΑ(432) νὰ θεωρηθεῖ ὅτι εἶναι ἡ νότα ΣΟΛ(770), σὰν ἡ πιὸ κοντινὴ στὴν δωδεκατονική μουσικὴ κλίμακα, αὐτὸ σωστὰ δὲν ἔγινε. Δὲν ἔγινε γιατὶ ἁπλὰ ἡ 7η ἁρμονικὴ τῆς νότας ΛΑ(432) εἶναι ἡ νότα ΣΟΛ-(755) τῆς ὁλοκληρωμένης μουσικῆς κλίμακας τοῦ ἀριθμοῦ φ, τῶν τριάντα ἕξι φθόγγων. Αὐτὸ ἴσως ἀποτελεῖ καὶ τὴν πειστικώτερη ἀπάντηση γιὰ τὴν ὕπαρξη καὶ τὴ σχέση τῆς 7ης ἁρμονικῆς συχνότητας τῆς θεωρίας τῶν στάσιμων κυμάτων μὲ τὴ θεμελιώδη μουσικὴ κλίμακα.

