Τετρακτὺς καὶ Πυθαγόρεια Μουσική Κλίμακα
Μουσικὸς κῶνος
Ἀπό τὸ βιβλίο…

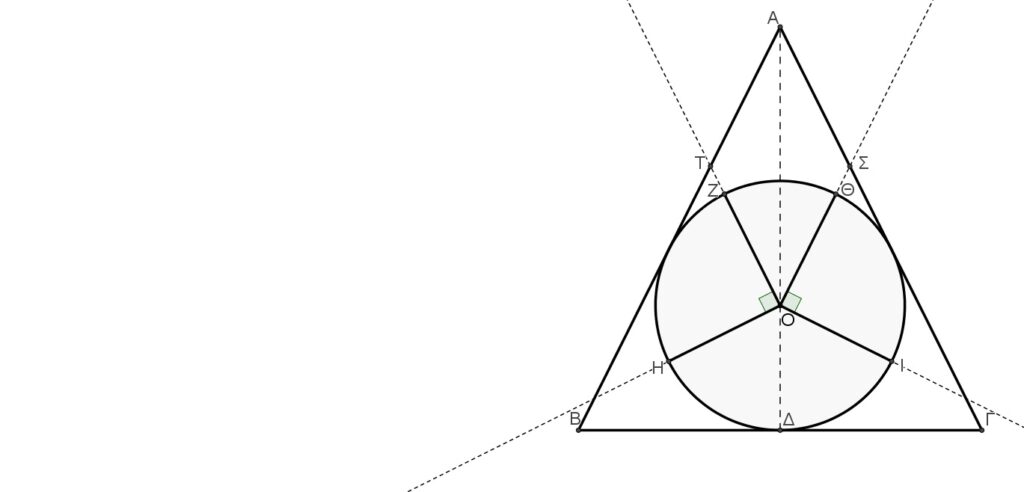
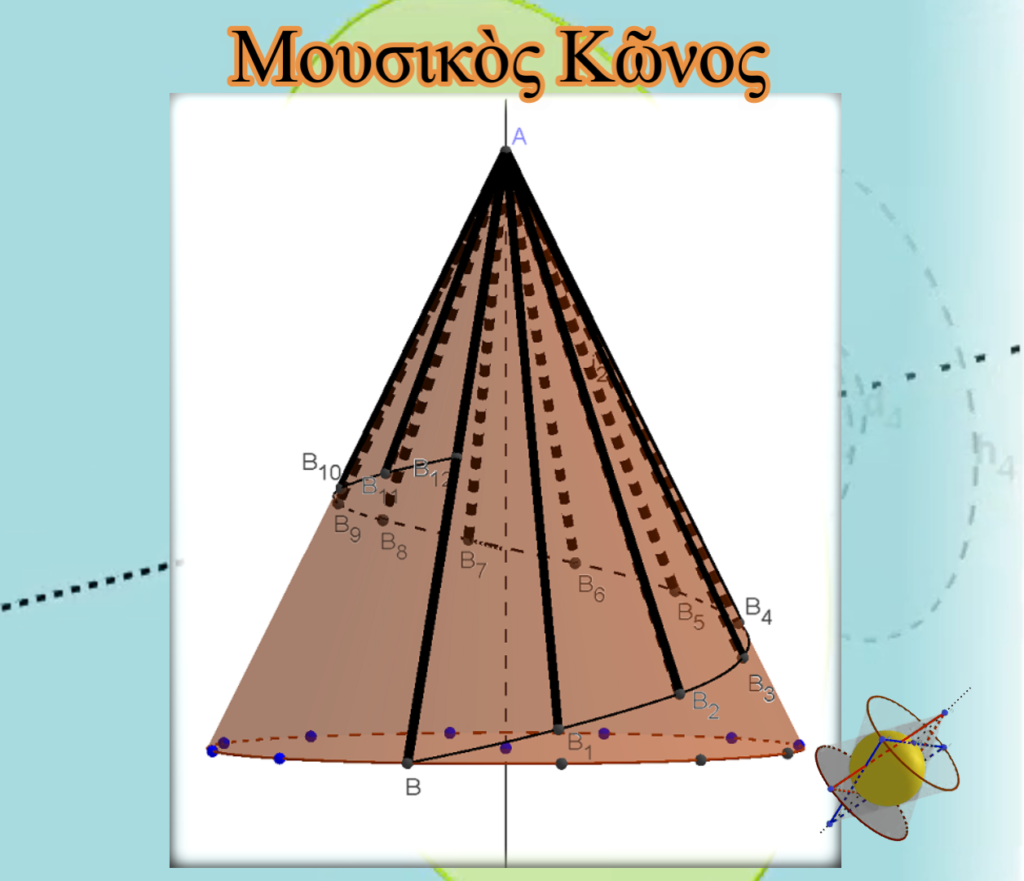
Εἴδαμε λοιπὸν μὲ ποιὸν τρόπο ὁ ἐνδιάμεσος ἀριθμὸς δ διαίρεσε τὴν κυκλικὴ βάση τῆς τρισδιάστατης Τετρακτύος σὲ δώδεκα ἴσα τόξα καὶ πὼς συνδέσαμε αὐτὸ μὲ τὴν ἐπινόηση τοῦ Ἱππάρχου νὰ χωρίσει τὸν κύκλο σὲ 360°. Ἂς ἐπιστρέψουμε στὴν μουσικὴ κλίμακα καὶ ἂς θεωρήσουμε ὅτι τὸ μῆκος τῆς πλευρᾶς τοῦ κώνου ΑΒ=λ εἶναι μιὰ χορδὴ ποὺ παράγει ἦχο συγκεκριμένης συχνότητας. Ἡ ἑπόμενη συχνότητα τῆς κλίμακας μας θὰ παράγεται ἀπὸ μία διπλανὴ χορδὴ ΑΒ1 ποὺ θὰ ἔχει μῆκος κατὰ 1,060660172… μικρότερο τῆς ΑΒ καὶ θὰ σχηματίζει γωνία μὲ τὴν ΑΒ ἴση μὲ 13,1416°, κατὰ τὴν ἀνάπτυξη τοῦ κώνου. Αὐτὴ τὴ χορδὴ μᾶς τὴν ἔδωσε ἡ Τετρακτύς καὶ εἶναι ἴση μὲ τὸ ΑΚ εὐθύγραμμο τμῆμα της. Ἡ ἐπανάληψη αὐτῆς τῆς πράξης ἄλλες ἕνδεκα φορὲς θὰ μᾶς ἀναπτύξει πλήρως τὴ μουσικὴ κλίμακα, ἡ ὁποία θὰ στηρίζεται στὴν Πυθαγόρεια Μουσικὴ Κλίμακα καὶ θὰ ἔχει χαρακτηριστικὰ γεωμετρικῆς προόδου, ὅπως ἡ Τετρακτὺς μᾶς ὑπέδειξε. Ἡ τελευταία μουσικὴ χορδή, ἡ ΑΒ12 , θὰ βρίσκεται πάνω στὴν ἴδια ἡμιευθεία μὲ τὴν ΑΒ χορδή, θὰ ἔχει μῆκος κατὰ 2,02728653… μικρότερο ἀπὸ τὴν ΑΒ καὶ θὰ παράγει συχνότητα ἤχου κατὰ 2,02728653… ὑψηλότερη τῆς χορδῆς ΑΒ.
Αὐτὸ τὸ φανταστικὸ μουσικὸ ὄργανο θὰ μπορούσαμε νὰ τὸ «βαφτίσουμε» καὶ σὰν Πυθαγόρειο Μουσικὸ Κῶνο.
Ὑπάρχουν ὅμως κάποια κενά.
Τὸ πρῶτο κενὸ εἶναι ὅτι, ἂν καὶ ἡ Τετρακτύς μᾶς δίνει τὴν ἀναλογία 2:1 καὶ μάλιστα μὲ σταθερὸ σημεῖο, τὴν κορυφὴ Α, (ΑΜ=2ΑΠ) (ἐδῶ), αὐτὸ δὲν προκύπτει στὴν μουσικὴ κλίμακα. Ἐὰν δηλαδὴ ξεκινούσαμε τὸν μουσικὸ κῶνο μὲ χορδὴ ἴση μὲ ΑΜ, δὲν θὰ καταλήγαμε σὲ χορδὴ ἴση μὲ τὴν μισὴ της καὶ ἑπομένως, οὔτε σὲ διπλάσια συχνότητα. Ἡ ἐπίτευξη τῆς διπλάσιας συχνότητας στὴν τελευταία νότα τῆς κλίμακας, σὲ σχέση μὲ τὴν πρώτη, πραγματοποιήθηκε, ὅπως εἴδαμε, μὲ ἀντικατάσταση τῆς τιμῆς τοῦ μεγάλου ἡμιτονίου (1,067871…) μὲ τὴν τιμὴ τοῦ μικροῦ ἡμιτονίου (1,05349794…), κατὰ τὴ μετάβαση μας σὲ αὐτήν. Μὲ αὐτὸν τὸν τρόπο ὅμως, δὲν τηρεῖται ὁ κανόνας τῆς γεωμετρικῆς προόδου, δηλαδὴ ὁ σταθερὸς λόγος συχνοτήτων γιὰ δύο συνεχόμενες νότες. Αὐτὸ ποὺ ἡ πυθαγόρεια μουσικὴ κλίμακα μᾶς ὑπέδειξε εἶναι πὼς ἐφόσον θέλουμε νὰ ἔχουμε σταθερὸ λόγο συχνοτήτων αὐτὸς θὰ ἔχει τὴν τιμὴ ΑΒ/ΑΚ=√(9/8)=1,06066… Ἡ τιμὴ αὐτὴ μᾶς ὑποδείχθηκε, σὰν μοναδικὴ ἐπιλογὴ δώδεκα ὅμοιων βημάτων ὁλοκλήρωσης τοῦ κύκλου τῆς συγκεκριμένης μουσικῆς κλίμακας. Ἡ παράπλευρη ἐπιφάνεια τοῦ κώνου, ποὺ προέκυψε ἀπὸ τὴν Τετρακτύν, μᾶς ὑπέδειξε τὰ δώδεκα βήματα ποὺ πρέπει νὰ πραγματοποιηθοῦν γιὰ τὴν ὁλοκλήρωση ἑνὸς κύκλου τοῦ φαινομένου. Ὁ λόγος ΑΒ/ΑΚ τῆς Τετρακτύος, μᾶς ὑπέδειξε τὴν ἀναγκαιότητα ὕπαρξης γεωμετρικῆς προόδου γιὰ τὴν ἀνάπτυξη τῆς μουσικῆς ἀκολουθίας.
Ὁ σκοπὸς λοιπὸν τῆς Τετρακτύος κατὰ τὴν ἐμφάνιση τῆς πυθαγόρειας μουσικῆς κλίμακας δὲν εἶναι νὰ μᾶς δώσει ἀκέραιο τὸν διπλασιασμὸ τῆς συχνότητας μὲ τὴν ὁλοκλήρωση τοῦ κύκλου. Ἡ κλίμακα ἀποδίδεται σὰν φυσικὸ ἐξελικτικὸ φαινόμενο, ἄρα σὲ αὐτὴν ὑποχρεωτικὰ ὑπεισέρχεται καὶ ὁ παράγοντας χρόνος. Τὴν τεράστια σημασία αὐτοῦ θὰ τὴν δοῦμε στὴν παρουσίαση τοῦ συμπαντικοῦ μοντέλου ποὺ στηρίζεται στὴν Τετρακτύν.
Πάραυτα, ἐὰν θέλουμε νὰ φέρουμε τὸν μουσικὸ κῶνο στὰ μέτρα τοῦ τρισδιάστατου κόσμου ποὺ ἀντιλαμβανόμαστε, θὰ πρέπει νὰ διορθώσουμε τὸν λόγο τῶν μηκῶν δύο συνεχόμενων χορδῶν ἀντικαθιστώντας τον μὲ τὴν τιμὴ 12√2=1,059463094…
Βλέπουμε λοιπὸν ὅτι ἡ Πυθαγόρεια μουσικὴ κλίμακα μᾶς ὁδήγησε ἐπίσης στὴν ἰσχύουσα μουσικὴ κλίμακα, ἀλλὰ σαφῶς μὲ μιὰ καλύτερη προσέγγιση ἀπὸ αὐτὴν τῶν στάσιμων κυμάτων.Ἡ ἀπόκλιση εἶναι:
(ΑΒ/ΑΚ)/12√2=(1,060660172…)/(1,059463094…)=1,0011299…
Μπορεῖ νὰ ὑπάρχει ἄλλος μουσικὸς κῶνος, συμβατὸς μὲ τὸν προαναφερόμενο;

