Τετρακτὺς καὶ Πυθαγόρεια Μουσική Κλίμακα
Μουσικός κῶνος 2
Ἀπό τὸ βιβλίο…

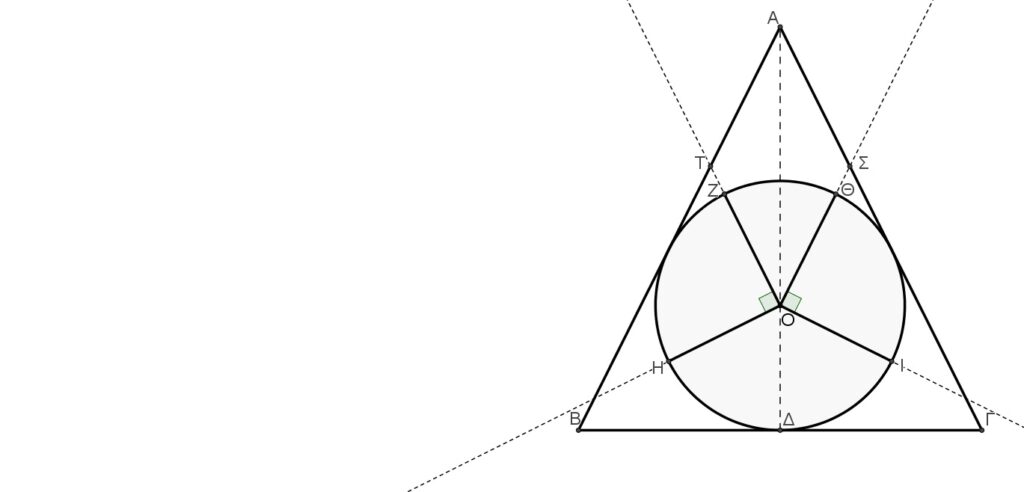
Ὅπως εἴδαμε, ὁ μουσικὸς κῶνος στηρίζεται στὸ Χρυσὸ Τρίγωνο (ΑΒΓ) ὅπου τὸ ὕψος (ΑΔ) πρὸς τὴ βάση του εἶναι ἴσο μὲ τὴν βάση (ΑΔ). Αὐτό, χωρίζει τὸ Χρυσὸ Τρίγωνο σὲ δύο ἴσα μεταξὺ τούς ὀρθογώνια τρίγωνα. Ἐὰν τὸ ὕψος ΑΔ εἶναι ἴσο μὲ φ, τότε ἡ ἄλλη κάθετη πλευρὰ θὰ εἶναι ἴση μὲ φ/2, ἐνῶ ἡ ὑποτείνουσα ὑπολογίζεται καὶ βρίσκεται ὅτι ἰσοῦται μὲ ΑΓ=(φ2+1)/2
Ἡ γωνία ΑΒ ̂Δ θὰ ἰσοῦται μὲ 63,435…°
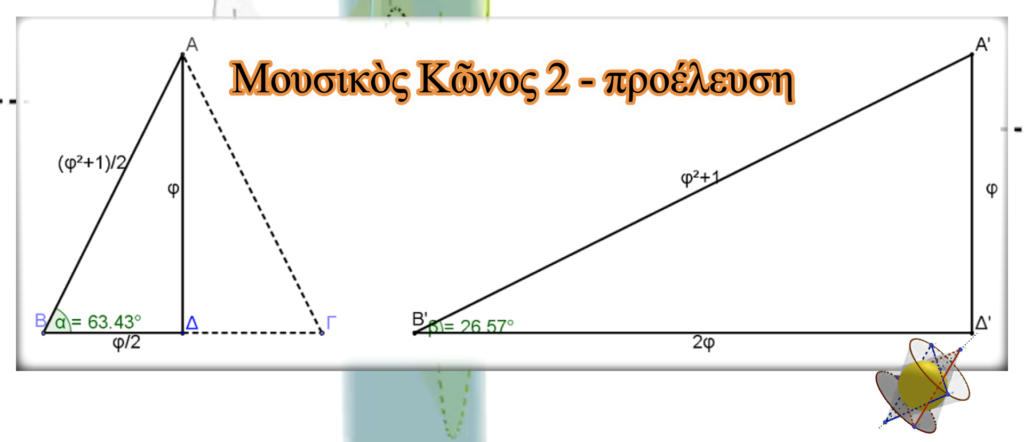
Θὰ ὁρίσουμε τώρα ἕνα νέο τρίγωνο ὅμοιο μὲ τὸ προηγούμενο. Σὲ αὐτό, ἡ μία κάθετη πλευρὰ θὰ ἰσοῦται πάλι μὲ φ (ΑΔ=Α’Δ’=φ). Αὐτὴ ὅμως θὰ εἶναι ἡ μικρὴ κάθετη πλευρά. Τότε, ἡ μεγάλη κάθετη πλευρὰ θὰ εἶναι διπλάσια (Β΄Δ΄=2φ). Σὲ αὐτὴν τὴν περίπτωση, ἡ γωνία Α’Β’ ̂Δ΄ θὰ εἶναι συμπληρωματικὴ τῆς ΑΒ ̂Δ .
Ἡ ὑποτείνουσα Α΄Β΄ τοῦ ὀρθογωνίου τριγώνου Α΄Δ΄Β΄, μὲ τὴ χρήση τοῦ πυθαγόρειου θεωρήματος ὑπολογίστηκε καὶ βρέθηκε ὅτι εἶναι διπλάσια τοῦ ΑΒ. (Α΄Β΄=2AB=φ2+1)
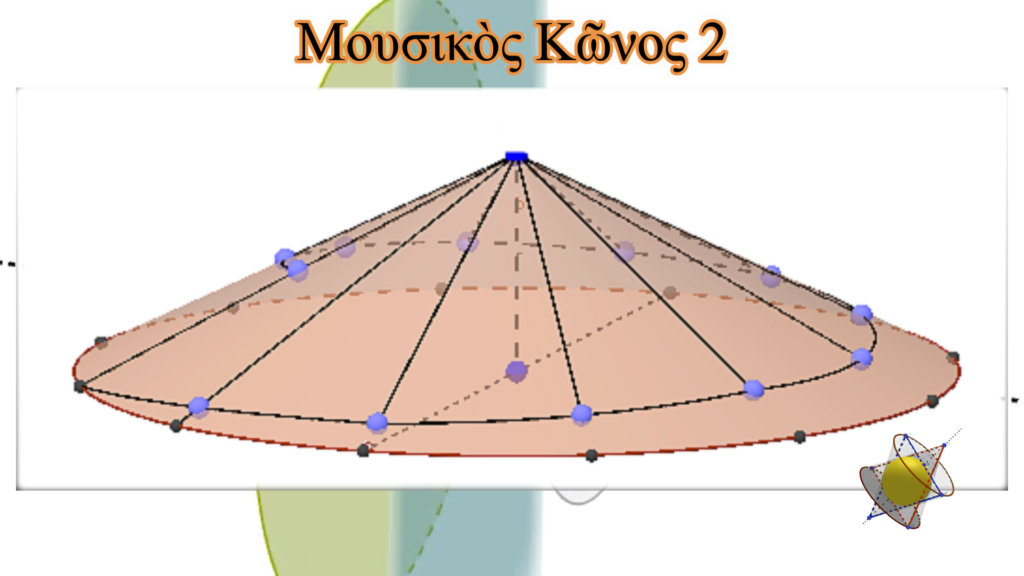
Ἐὰν τώρα περιστρέψουμε τὸ τρίγωνο Α΄Δ΄Β΄ γύρω ἀπὸ τὸν ἄξονα Α΄Δ΄, θὰ προκύψει ἕνας νέος κῶνος. Ἡ πλευρὰ αὐτοῦ θὰ εἶναι διπλάσια τοῦ ἀρχικοῦ κώνου, ὁπότε, σὲ ἀναλογία μὲ τὸν ἀρχικό, σὰν μουσικὸς κῶνος θὰ μποροῦσε νὰ παράγει τὴν ἴδια μουσικὴ κλίμακα, ἀλλὰ κατὰ μία ὀκτάβα χαμηλότερα. Θὰ εἶναι δηλαδὴ ἕνας μουσικὸς κῶνος ἀπόλυτα συμβατὸς μὲ τὸν ἀρχικό.
Ἂς διερευνήσουμε περαιτέρω τὸν νέο μουσικὸ κῶνο καὶ κατὰ ἀναλογία μὲ τὸν ἀρχικό, ἂς τὸν ἀναπτύξουμε σὲ δύο διαστάσεις. Ἔτσι, θὰ προκύψει ὁ παρακάτω κυκλικὸς τομέας.
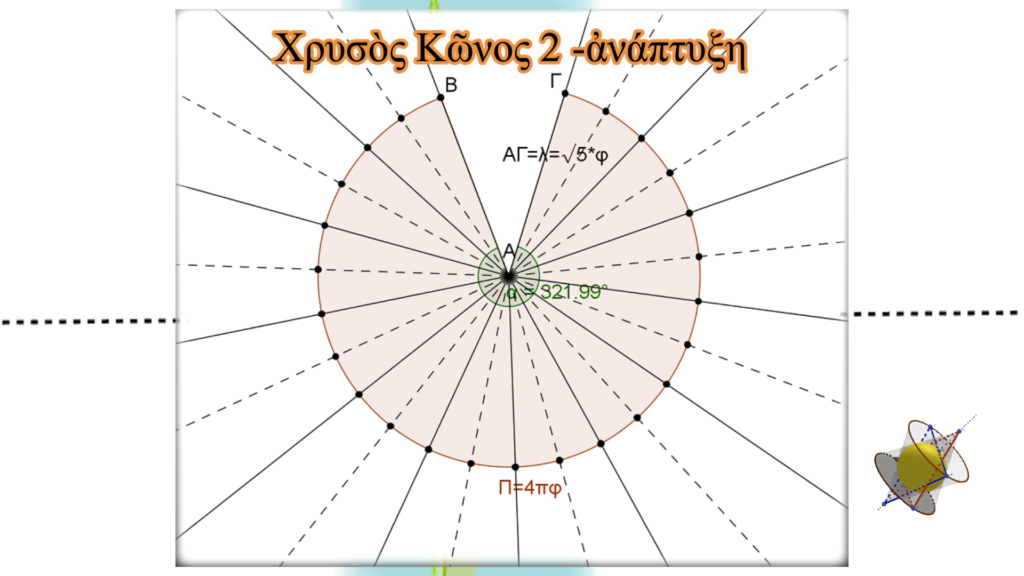
Ἡ ἀκτίνα του, ΑΓ εἶναι ἴση μὲ τὴν ὑποτείνουσα τοῦ ὀρθογωνίου τριγώνου Α΄Δ΄Β΄ ΑΓ=√5∙φ=φ2+1=3,618034…
Ἡ περίμετρος τοῦ τόξου ΒΓ εἶναι ὅση καὶ ἡ περίμετρος τοῦ κύκλου τῆς βάσης τοῦ μουσικοῦ κώνου καὶ ἰσοῦται μὲ : Π=4πφ
Ἡ ἀντίστοιχη ἐπίκεντρη γωνία εἶναι: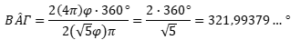
Ἡ γωνία αὐτὴ εἶναι διπλάσια τῆς ἀντίστοιχης ἐπίκεντρης γωνίας τοῦ ἀρχικοῦ μουσικοῦ κώνου.
Διαιρώντας τὴν γωνία σὲ δώδεκα ἴσες γωνίες τῶν 321,99379/12=26,83281…° παίρνουμε τὰ δώδεκα βήματα τῆς μουσικῆς κλίμακας τοῦ μουσικοῦ κώνου 2 ἢ τοῦ ὅποιου ἄλλου ἁρμονικοῦ ἐξελικτικοῦ φαινομένου μπορεῖ νὰ περιγραφεῖ μὲ αὐτὸν τὸν τρόπο.
Ἐὰν θεωρήσουμε τὴ γωνία αὐτὴν σὰν τὸ ἄθροισμα δύο ἐπίκεντρων γωνιῶν τοῦ ἀρχικοῦ μας κώνου, τότε μποροῦμε νὰ τὴν διαιρέσουμε σὲ εἴκοσι τέσσερις ἴσες γωνίες τῶν 13,4164…°. Ἔτσι καταλήγουμε στὴν περιγραφὴ τοῦ πλέον χαρακτηριστικοῦ περιοδικοῦ φαινομένου τοῦ πλανήτη μας, τῆς περιστροφῆς του γύρω ἀπὸ τὸν ἑαυτὸ του. Ἔχουμε τὸν διαχωρισμὸ τοῦ φαινομένου σὲ δύο μέρη, (ἡμέρας, νύχτας) καὶ τὸ κάθε ἕνα σὲ δώδεκα ἐπιμέρους μέρη (ὧρες). Ὅλα αὐτὰ ἔρχονται βέβαια σὲ ἀπόλυτη ταύτιση μὲ τὸν ἐμπνευστὴ τοῦ συγκεκριμένου μοντέλου, τοῦ Ἱππάρχου.
Στὴ συνέχεια θὰ δοῦμε κάποια ἰδιαίτερα χαρακτηριστικὰ τῆς τιμῆς τῆς ἐπίκεντρης γωνίας τῶν 321,9937888…°.
