Τετρακτὺς καὶ Πυθαγόρεια Μουσική Κλίμακα
Μουσικός κῶνος 2 καὶ ἡ γνωστὴ Τετρακτύς
Ἀπό τὸ βιβλίο…

Ὅπως εἴδαμε, τὸ πλέον χαρακτηριστικὸ γνώρισμα τῆς Τετρακτύος εἶναι ἡ ἐμφάνιση τῶν δέκα πρώτων ἀκεραίων ἀριθμῶν. Μάλιστα τὸ ἄθροισμα τους μᾶς δίνει τὸν ἀριθμὸ 55, τοῦ ὁποίου τὸ ἄθροισμα τῶν ψηφίων ποὺ τὸν ἀπαρτίζουν δίνει ἐπίσης τὸν ἀριθμὸ 10. Ἐπίσης ὁ ἀριθμὸς 55 εἶναι ὁ δέκατος ὅρος τῆς σειρὰς Fibonacci.
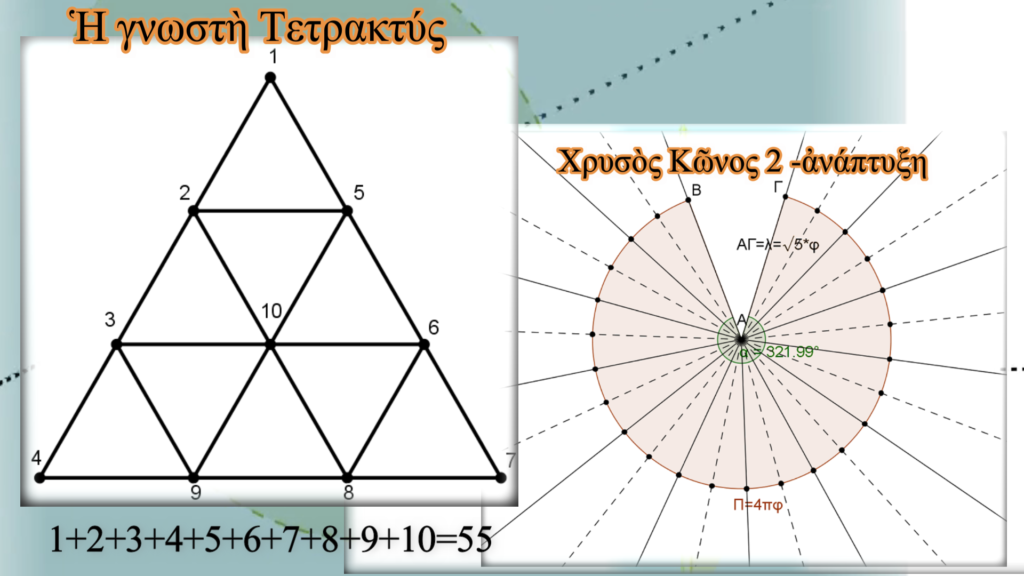
Αὐτὸν τὸν καθόλου τυχαῖο ἀριθμὸ θὰ τὸν προσθέσουμε στὴν τιμὴ τῆς ἐπίκεντρης γωνίας τοῦ κυκλικοῦ τόξου ποὺ ἀντιστοιχεῖ στὸν μουσικὸ κῶνο 2. Ἔτσι ἔχουμε :
ô+55=321,9937888…+55=376,9937888…
Εἶναι μιὰ τιμὴ πολὺ κοντὰ στὴν τιμὴ ποὺ προέκυψε ἀπὸ τὸν πολλαπλασιασμὸ τῆς ἐπίκεντρης γωνίας μὲ τὴν τιμὴ φ2/√5=1,1708204…
321,9937888…∙1,1708204…=376,9968944…
Εἶναι λοιπὸν φανερὸ ὅτι μὲ τὴν πρόσθεση τοῦ ἀριθμοῦ 55 στὴν ἐπίκεντρη γωνία, καταλήγουμε σχεδὸν στὴν ἴδια γωνία, ἡ ὁποία, διαιρούμενη μὲ τὸν ἀριθμὸ 12 καὶ κατόπιν μὲ τὸν ἀριθμὸ 10, μᾶς δίνει μία τιμὴ ἀνάμεσα στοὺς ἀριθμοὺς π καὶ πφ.
376,9937888/120=3,141614906…
Ἡ διαφορὰ μεταξὺ τῶν δύο τιμῶν ποὺ προκύψανε εἶναι καὶ πἀλι ἴση με τὴν τιμἠ φ-12
376,9968944…-376,9937888…=0,00310562…=φ-12 ἀλλὰ καὶ
377-376,9968944…=0,00310562…=φ-12, ὅπως ἀκριβῶς καὶ μὲ τὴν διαφορὰ τῆς τιμῆς τῆς ἐπίκεντρης γωνίας καὶ τῆς τιμῆς τοῦ ὅρου φ12.

