Τετρακτὺς καὶ Πυθαγόρεια Μουσική Κλίμακα
Ὁ βηματισμὸς τῆς Πυθαγόρειας Μουσικῆς Κλίμακας
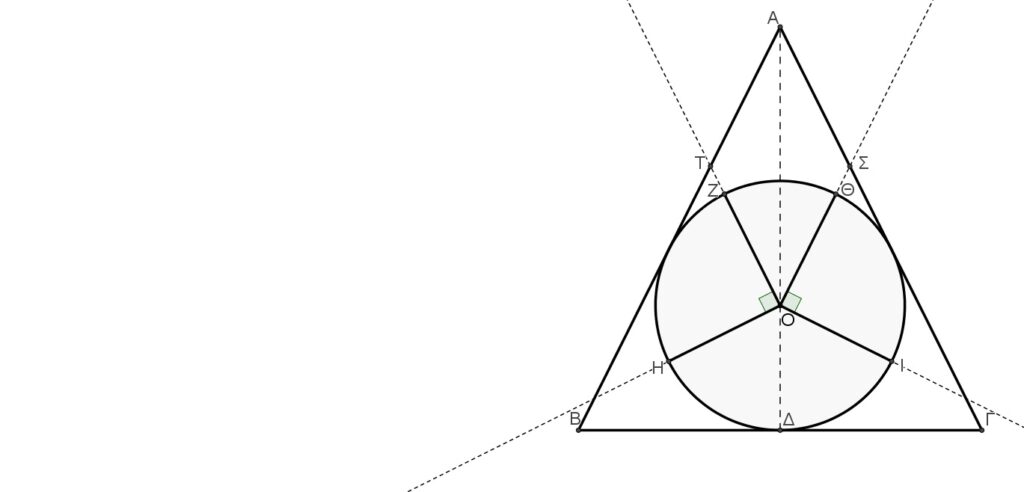
Ἀπό τὸ βιβλίο…

Θὰ προχωρήσουμε τώρα στὴν πιὸ σημαντικὴ πληροφορία ποὺ μπορεῖ νὰ μᾶς δώσει ἡ Τετρακτύς γιὰ τὴν Πυθαγόρεια Μουσικὴ κλίμακα, ὅταν αὐτὴν θὰ τὴν ἀποδεχτοῦμε μὲ τὴν μορφὴ τοῦ Χρυσοῦ Τριγώνου.
Ἀρχικά, στὸν ἑπόμενο πίνακα θὰ παρουσιάσουμε τὴν Μουσικὴ κλίμακα τῆς νότας Λα σὰν ἐξελικτικὸ φαινόμενο, ὅπου σέ κάθε βῆμα, ἡ συχνότητα τῆς ἑπόμενης νότας θὰ ἰσοῦται μὲ τὰ 3/2 τῆς προηγούμενης, καθ’ ὑπόδειξη τοῦ Πυθαγόρα. Τὶς προκύπτουσες συχνότητες καὶ ὅπου χρειάζεται, θὰ τὶς ἀνάγουμε σὲ ἀντίστοιχες συχνότητες ὅμοιας αἰσθητικῆς ἀξίας καὶ ἐντὸς εὔρους συχνοτήτων τῆς ἀρχικῆς ὀκτάβας [432 – 864(875,79)], διαιρώντας τὶς τιμὲς ποὺ προκύπτουν μὲ τὴν κατάλληλη δύναμη τοῦ ἀριθμοῦ 2. Θὰ τὶς τοποθετήσουμε στὸν πίνακα μὲ αὔξουσα σειρά. Τὴ μουσικὴ κλίμακα ποὺ προκύπτει θὰ τὴν ὀνομάσουμε πυθαγόρεια, πρὸς τιμὴ του, ἀλλὰ καὶ γιὰ νὰ τὴν ξεχωρίσουμε ἀπὸ αὐτὴ ποὺ προκύπτει ἀπὸ τὴ θεωρία τῶν στάσιμων κυμάτων.
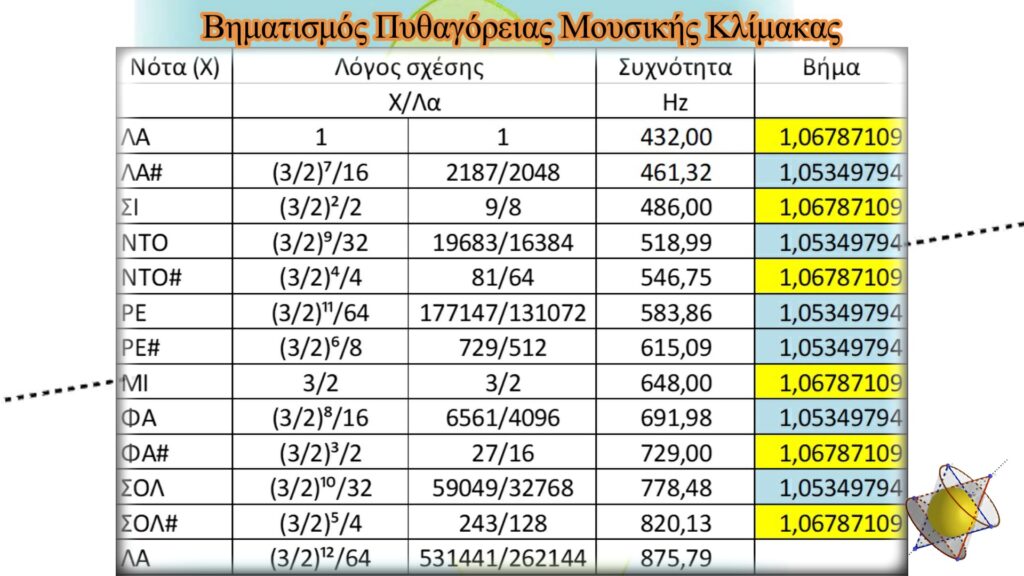
Στὴν τελευταία στήλη, σὰν βῆμα δίνεται ὁ λόγος τῶν δύο συνεχόμενων συχνοτήτων τῆς κλίμακας.
Αὐτὸ ποὺ μποροῦμε νὰ παρατηρήσουμε εἶναι ὅτι ἔχουμε δύο διαφορετικὰ βήματα, ἡμιτόνια, μὲ μικρὴ διαφορὰ τιμῆς μεταξὺ τους (1,053497972… καὶ 1,067871094…). Τὰ δύο ἡμιτόνια ἐναλλάσσονται μέχρι τὴ μέση τῆς κλίμακας. Ἐκεῖ ἀλλάζει ἡ σειρὰ ἐναλλαγῆς τους καὶ ἔτσι συνεχίζει μέχρι νὰ ὁλοκληρωθεῖ ἡ κλίμακα.
Λόγος συχνοτήτων ἀρχικῆς – τελικῆς νότας ὀκτάβας
Ὅπως ἤδη ἔχει εἰπωθεῖ, ὁ ἐπιθυμητὸς λόγος συχνοτήτων τῆς τελικῆς νότας ἀπὸ τὴν ἀρχικὴ νότα τῆς κλίμακας εἶναι 2. Κατὰ τὴν Πυθαγόρεια Μουσικὴ Κλίμακα ὅμως, αὐτὸς εἶναι 875,79/432=2,02728653…
Ποιὸς λόγος ἀπὸ τοὺς δύο εἶναι ἀποδεκτός;
Ἡ ἀπάντηση ποὺ θὰ μπορούσαμε νὰ δώσουμε εἶναι ὅτι καὶ οἱ δύο λόγοι εἶναι ἀποδεκτοί. Ἡ πρώτη περίπτωση, γιὰ τιμὴ τοῦ λόγου ἴση μὲ 2, ἔχει ἐφαρμογὴ ὅταν ὁ ἦχος δημιουργεῖται, διαδίδεται καὶ γίνεται ἀντιληπτὸς ἐντὸς συγκεκριμένων ὁρίων. Ἡ δεύτερη πάλι περίπτωση, θὰ λέγαμε ὅτι εἶναι σωστὴ καὶ ὅτι ἔχει ἐφαρμογὴ σὲ περιπτώσεις ἀβίαστης δημιουργίας καὶ διάδοσης τῶν κυμάτων.
Πὼς ὅμως ἀπὸ τὴν Πυθαγόρεια κλίμακα θὰ μπορούσαμε νὰ φτάσουμε στὴν τιμὴ 2;
Γιὰ τὴν εὕρεση τοῦ ἀριθμοῦ π ἀπὸ τὸν ἀριθμὸ φ, ὅταν θελήσαμε νὰ τοποθετήσουμε τὴν ἀκολουθία Δν=δ·φν ἐντὸς ὁρίων, ψαλιδίσαμε τὴν τιμὴ Δ12=432,0041666… στὴν τιμὴ 432 ἀφαιρώντας τὴν τιμὴ τοῦ ὅρου Δ-12.
Αὐτὸ θὰ κάνουμε καὶ στὴν Πυθαγόρεια κλίμακα. Ἔτσι, στὸν προηγούμενο πίνακα, ἀντὶ ἀπὸ τὴν ΣΟΛ# (820,13Hz), νὰ πᾶμε στὰ 875,79 Hz, θὰ πᾶμε στὰ 864Hz καὶ αὐτὴ τὴ συχνότητα θὰ ὀνομάσουμε ΛΑ. Ὁπότε ὁ λόγος μας θὰ εἶναι 864/432=2. Φαντάζει αὐθαίρετο καὶ φαινομενικὰ ἰδιαίτερα ἁπλουστευμένο γιὰ νὰ γίνει εὔκολα ἀποδεκτό. Πολλὲς φορὲς ὅμως μέσα ἀπὸ τὴν ἁπλότητα ξεπροβάλλουν τὰ πιὸ ὄμορφα πράγματα. Ποιὰ εἶναι αὐτὰ στὴν περίπτωση μας;
Ἀρχικὰ εἶναι ὁ νέος λόγος
ΛΑ/ΣΟΛ# = 864,00/820,13…=1,053497942…
Βλέπουμε ὅτι, ἂν γιὰ τὸ τελευταῖο βῆμα τῆς Πυθαγόρειας κλίμακας, ἐπιλέξουμε τιμὴ ἴση μὲ τὸ μικρὸ ἡμιτόνιο ἀντὶ τοῦ μεγάλου, αὐτόματα ἡ κλίμακα μας συμπληρώνεται μὲ συχνότητα διπλάσια τῆς ἀρχικῆς, ἐκπληρώνοντας ἔτσι τὴν συγκεκριμένη ἀπαίτηση.
Συμπληρώνουμε ξανὰ τὸν προηγούμενο πίνακα ξεκινώντας αὐτὴ τὴν φορὰ τὴν κλίμακα ἀπὸ τὴ νότα ΦΑ# (729,00Hz) γιὰ ἐναρμονισμό σὲ δεδομένα ποὺ ἐπιθυμοῦμε νὰ καταλήξουμε. Μὲ βάση τὰ προηγούμενα, ἀντικαθιστοῦμε τὶς τιμὲς στὴν τελευταία σειρά. Προσθέτουμε μιὰ ἀκόμα στήλη στὴν ὁποία ζωγραφίζουμε λευκὸ τὸ κάθε κελὶ ποὺ ἀντιστοιχεῖ σὲ βῆμα μικροῦ ἡμιτονίου καὶ μαῦρο τὸ κελὶ ποὺ ἀντιστοιχεῖ σὲ βῆμα μεγάλου ἡμιτονίου. Τὸ ἀποτέλεσμα εἶναι ἁπλὰ ἐκθαμβωτικό. Σχηματίστηκαν σὲ σειρὰ καὶ ἀριθμὸ τὰ πλῆκτρα ποὺ συμπληρώνουν μιὰ ὀκτάβα σὲ πιάνο. Τὸ κάθε πλῆκτρο ἀντιστοιχεῖ στὴν νότα τῆς ἴδιας σειρᾶς τῆς πρώτης στήλης. Ἡ σύμπτωση, ἐὰν πρόκειται γιὰ σύμπτωση, τουλάχιστον προβληματίζει.
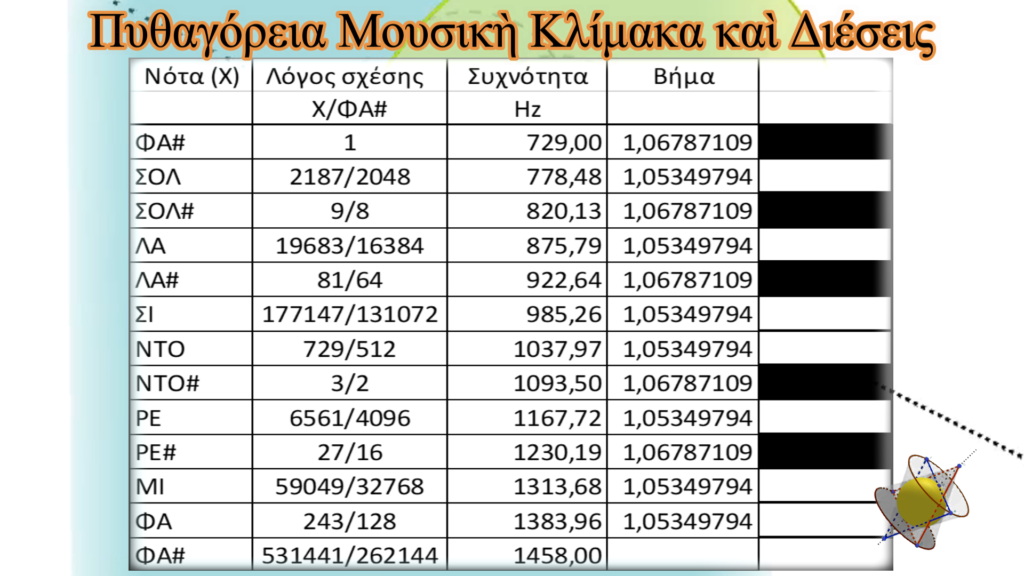
Αὐτὴ εἶναι ἡ ἀρχικὴ πρόταση τῆς Πυθαγόρειας Μουσικῆς Κλίμακας γιὰ τὴν περίπτωση ὅπου κινούμαστε ἐντὸς ὁρίων (τιμὴ λόγου ἴση μὲ δύο).
Ὁ λόγος ΑΒ/ΑΚ καὶ ἡ τιμή του (√(9/8) =1,060660172…)
Συνεχίζουμε μὲ τὴν περίπτωση ὅπου ὁ λόγος συχνοτήτων τελικῆς – ἀρχικῆς νότας ἰσοῦται μὲ 2,02728653… τὸν ὁποῖο ἐπίσης θεωροῦμε ἀποδεκτό. Τότε ὅμως, ὅπως ἔγινε καὶ στὴν σύγχρονη ἐποχὴ μὲ τὸν συγκερασμό, θὰ πρέπει τὸ κάθε ἐξελικτικὸ βῆμα τῆς μουσικῆς κλίμακας νὰ γίνεται μὲ μιὰ τιμὴ ἴση μὲ τὴν 12√2,02728653… Ἡ τιμὴ αὐτὴ ὑπολογίστηκε καὶ βρέθηκε ἴση μὲ 1,060660172…=√(9/8)
Ἔχουν σχέση οἱ δύο διαφορετικὲς τιμὲς τῶν ἡμιτονίων ποὺ προέκυψαν ἀπὸ τὴν Πυθαγόρεια Κλίμακα μὲ τὴν τιμὴ 1,060660172…=√(9/8) ;
Ἡ ἀπάντηση καὶ ἀναμενόμενη εἶναι καὶ καταφατικὴ. Ὁ ἀριθμὸς √(9/8)=1,060660172 εἶναι ὁ γεωμετρικὸς μέσος τῶν δύο τιμῶν τῶν ἡμιτονίων μὲ βάση τὴν Πυθαγόρεια Κλίμακα.
1,067871…·1,053498…=1,060660172…²=9/8
Ἡ καταφατικὴ ἀπάντηση συνηγορεῖ στὴν ἄποψη ὅτι ἡ ἀπόδοση τῆς μουσικῆς κλίμακας δίνεται μὲ μορφὴ γεωμετρικῆς προόδου. Τὴν κατεύθυνση αὐτὴ μᾶς τὴν ὑπέδειξε ἡ πυθαγόρεια κλίμακα. Ἡ Τετρακτύς θὰ μᾶς τὴν ἀναδείξει δίνοντας μας τὸν λόγο τῆς προόδου, τὸν βηματισμὸ δηλαδὴ τῆς μουσικῆς κλίμακας.
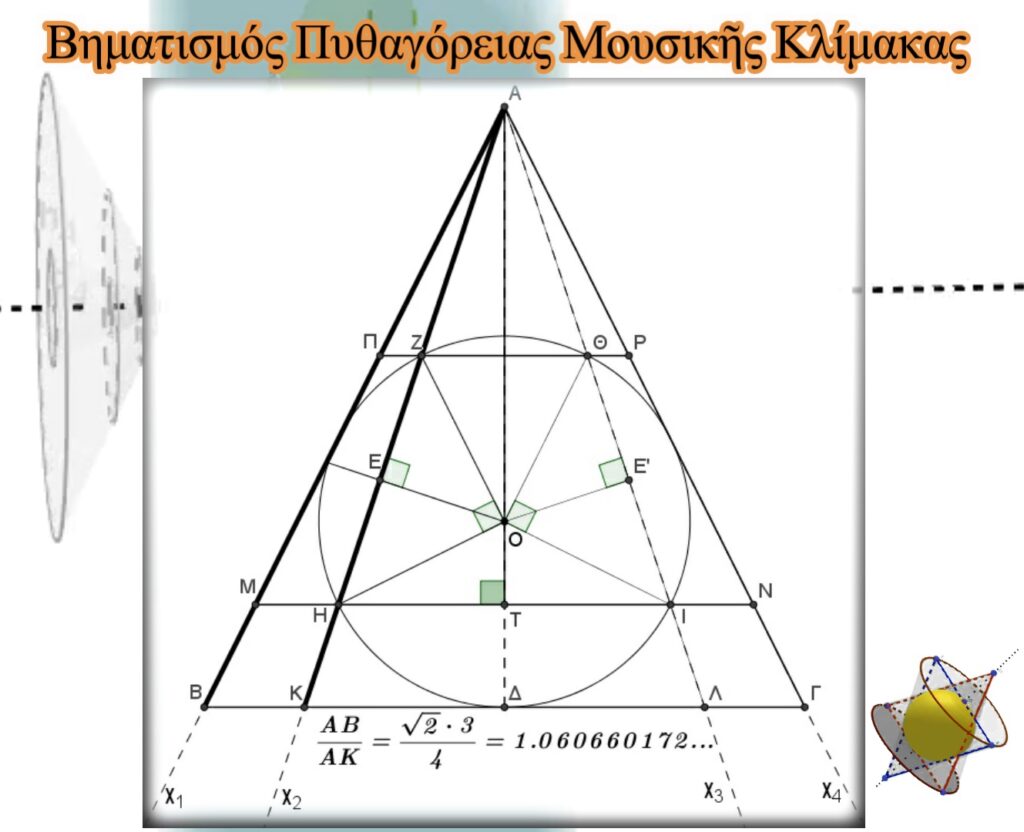
Ἀποδεικνύεται (ἐδῶ) ὅτι: ΑΒ/ΑΚ=1,060660172…
Βλέπουμε λοιπὸν ὅτι ὁ λόγος τῆς γεωμετρικῆς προόδου ποὺ θὰ πρέπει νὰ ἀποδίδει τὴν συγκεκριμένη Μουσικὴ Κλίμακα, ποὺ τὴν ὀνομάσαμε πυθαγόρεια, μᾶς δίνεται ἁπλούστατα καὶ ἐμφατικὰ μέσω τῆς Τετρακτύος. Μᾶς δίνεται σὰν λόγος δύο εὐθυγράμμων τμημάτων. Αὐτὰ τὰ εὐθύγραμμα τμήματα, σὰν θέση στὴν Τετρακτύν δὲν εἶναι τυχαία. Εἶναι δύο εὐθύγραμμα τμήματα τῶν ὁποίων τὰ σημεῖα Β καὶ Κ, μαζὶ μὲ τὸ μέσον Μ τοῦ ΒΓ εὐθύγραμμου τμήματος καθορίζουν τὰ εὐθύγραμμα τμήματα ΒΔ καὶ ΚΔ, ὅπως καὶ τὸν μεταξὺ τους λόγο (ΒΔ/ΚΔ=3/2). Ἂν αὐτὰ (τὰ ΑΒ καὶ ΑΚ τμήματα), τὰ θεωρούσαμε χορδὲς μουσικοῦ ὀργάνου, θὰ εἴχαμε δύο συνεχόμενες νότες μὲ λόγο ἴσο μὲ τὴν τιμὴ τοῦ ἡμιτονίου τῆς ἑνιαίας Πυθαγόρειας μουσικῆς κλίμακας (1,06066…). Ἡ ὕπαρξη τῶν δύο αὐτῶν εὐθυγράμμων τμημάτων μὲ τὸν δεδομένο λόγο στὸ σχέδιο τῆς Τετρακτύος, μᾶς ὑποδεικνύει γιὰ πρώτη φορὰ τὴν ὕπαρξη κλίμακας, σκάλας δηλαδὴ ποὺ τὴν ἀνεβαίνουμε σκαλί-σκαλί.
Ἡ Τετρακτύς ὅμως «φρόντισε» τὸν βηματισμὸ τῆς πυθαγόρειας κλίμακας νὰ τὸν δώσει καὶ σὰν τιμὴ εὐθυγράμμου τμήματος, ὅπως ἤδη προέκυψε κατὰ τὴν ἀπόδειξη εὔρεσης τῆς ἐνδιάμεσης τιμῆς δ. Γιὰ τὸ ΑΕ εὐθύγραμμο τμῆμα ἰσχύει (ἐδῶ):
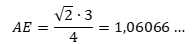
Αὐτό, μᾶς καταδεικνύει ἐμφατικὰ καὶ μὲ ἕναν ἀκόμη τρόπο, τὴ ταύτιση τοῦ χρυσοῦ τριγώνου μὲ τὸ σύμβολο τῆς Τετρακτύος.
Στὴν συνέχεια θὰ δοῦμε συγκεντρωτικὰ, ὅσα ἔως τώρα μᾶς ἀποκἀλυψε ἡ Τετρακτὐς
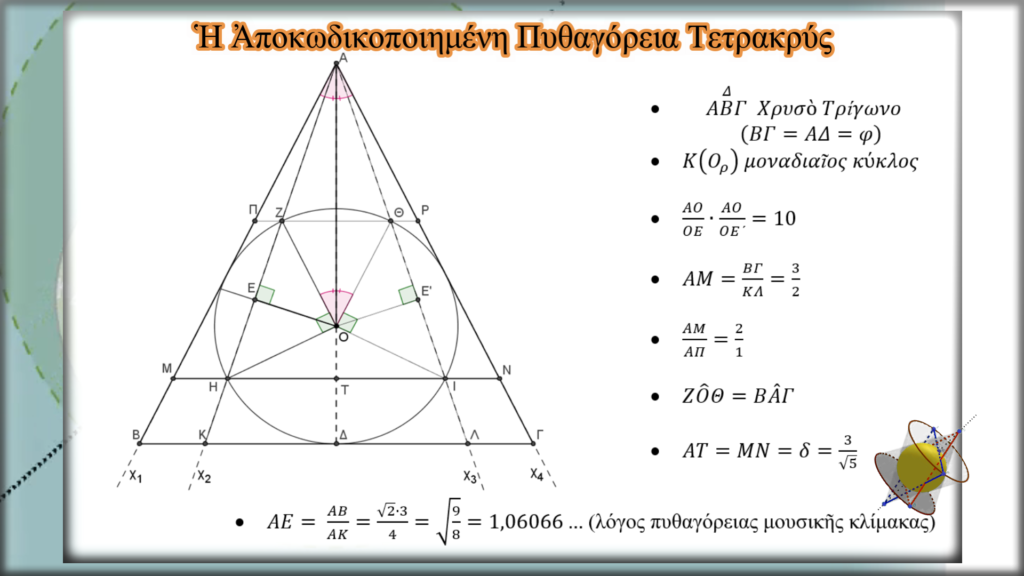
Φυσικὰ δὲν γνωρίζουμε καὶ οὔτε θὰ μπορούσαμε νὰ γνωρίζουμε μέχρι ποιοῦ σημείου ἀνάλυσης τῆς Τετρακτύος εἶχε φτάσει ὁ Πυθαγόρας, λόγῳ ἔλλειψης γραπτῶν κειμένων καὶ γνωστικῶν ἐργαλείων τῆς ἐποχῆς ποὺ ἔζησε. Ἔδωσε ὅμως σίγουρα τὴν βάση καὶ τὸ πεδίο ἔρευνας γιὰ τὴν ἐξέλιξη της μὲ μιὰ διαφορετικὴ προσέγγιση, κάτι τὸ ὁποῖο ἐδῶ πράττουμε.
Ὅτι ζητήσαμε λοιπὸν ἕως τώρα ἀπὸ τὴν Τετρακτύν, γιὰ νὰ τεκμηριώσουμε τὴν πυθαγόρεια μουσικὴ κλίμακα (ὅπως τὴν ὀνομάσαμε), μᾶς τὸ ἔδωσε. Δὲν μᾶς ἔδωσε ὅμως ἀκόμα τὸν ἀριθμὸ δώδεκα. Τὸν ἀριθμὸ τῶν βημάτων (ἡμιτονίων) ποὺ χρειάζονται γιὰ τὴν ὁλοκλήρωση τῆς μουσικῆς κλίμακας, τὴν ὁλοκλήρωση ἑνὸς κύκλου ὅπως λέμε μεταφορικά, ἀλλὰ καὶ στὴν πράξη ὅπως θὰ δοῦμε στὴ συνέχεια.
