Τετρακτὺς καὶ Πυθαγόρεια Μουσική Κλίμακα
Τετρακτὺς καὶ ἡ τιμὴ 3/2
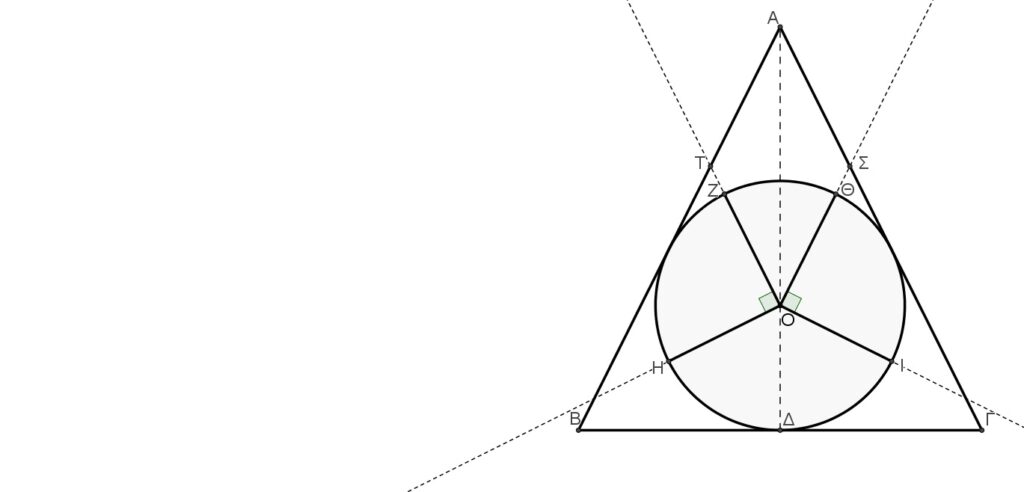
Ἀπό τὸ βιβλίο…

Ἡ Τετρακτύς, γιὰ νὰ ὁρίσει τὸν ἐνδιάμεσο ἀριθμὸ δ, ὅρισε τὸ ΜΝ εὐθύγραμμο τμῆμα καὶ ταυτόχρονα τὰ σημεῖα Μ καὶ Ν. Ἔτσι ὅμως ἐμφανίζεται τὸ εὐθύγραμμο τμῆμα ΑΜ, τὸ ὁποῖο θὰ ὑπολογίσουμε.
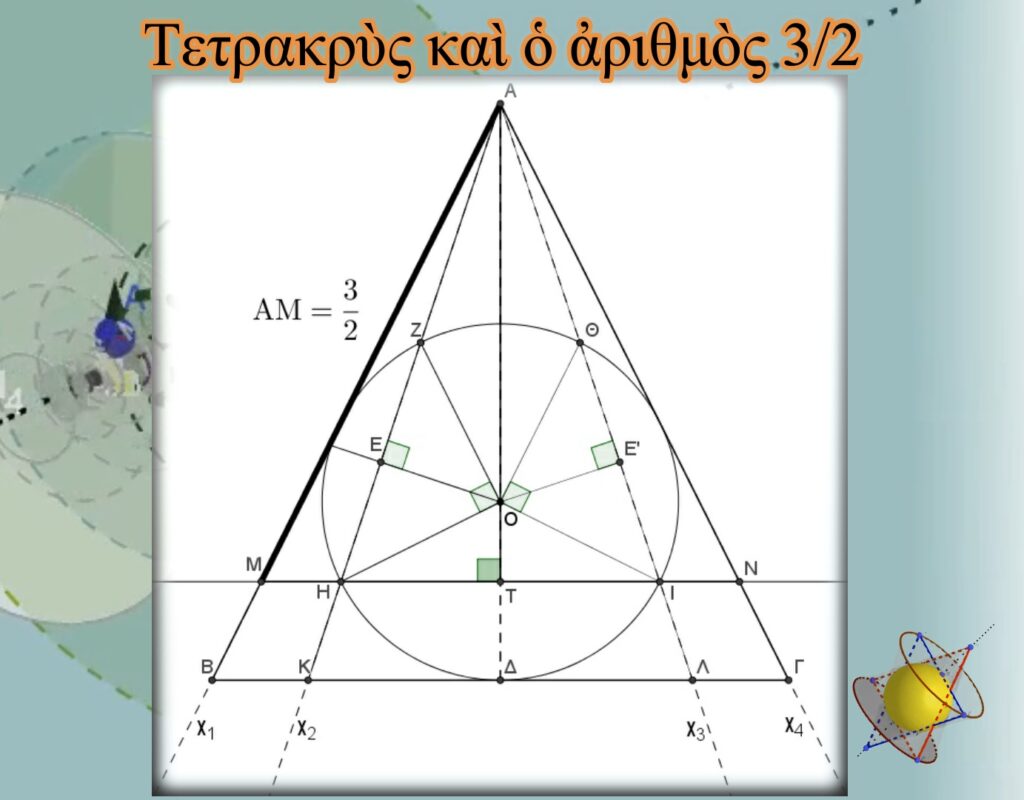
Ἀπὸ τὴν ἐμφανὴ ὁμοιότητα τῶν τριγώνων ΑΜΤ καὶ ΑΒΔ ἔχουμε:
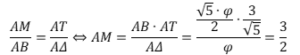
Βλέπουμε ὅτι ὁρίζοντας τὸν μοναδιαῖο κύκλο σὰν τὸν ἐγγεγραμμένο κύκλο τῆς Τετρακτύος, ὁρίζουμε καὶ τὴν Μονάδα. Αὐτή, θὰ ἰσοῦται μὲ τὴ διάμετρο τοῦ κύκλου. Ἔτσι, ἡ Τετρακτύς, πέρα ἀπὸ τὴν τιμὴ 3/2, ποὺ μᾶς ἔδωσε σὰν λόγο εὐθυγράμμων τμημάτων (ΒΓ/ΚΛ=3/2), τώρα μᾶς τὴν δίνει καὶ σὰν μέγεθος (ΑΜ=3/2).
Τετρακτὺς καὶ ὁ ἀριθμὸς 3/4
Ἐπίσης, μὲ τὴ βοήθεια καὶ τῶν δύο ἄλλων ἀκτίνων τῆς Τετρακτύος, ἐμφανίζεται ὁ μουσικὸς λόγος ΑΠ=ΠΜ=3/4, ὁ ὁποῖος εὔκολα ἀποδεικνύεται (ἐδῶ), ὅπως καὶ ὁ λόγος τῆς δεύτερης ἁρμονικῆς ΑΜ/ΑΠ=2/1.
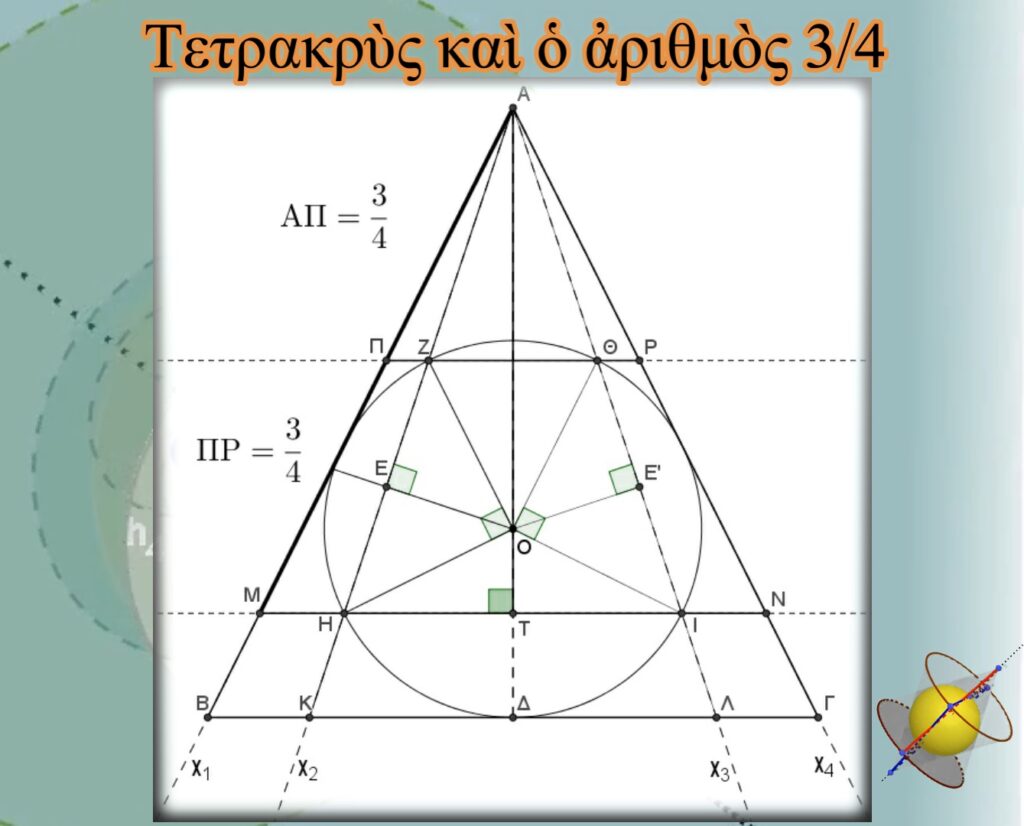
Τὴν τιμὴ ¾ θὰ τὴν δοῦμε νὰ ἐμφανίζεται ἀργότερα καὶ σὰν εὐθύγραμμο τμῆμα.
Ἔχουμε λοιπὸν ἕως τώρα τὴν ἐμφάνιση ὅλων τῶν δυνατῶν συνδυασμῶν τῶν τεσσάρων πρώτων ἀκεραίων ἀριθμῶν σὲ μορφὴ λόγων 1/2, 1/3, 2/3, 3/4. Εἶναι οἱ τέσσερις ἀριθμοὶ ποὺ τὸ ἄθροισμά τους μᾶς δίνει τὸν ἱερὸ ἀριθμὸ 10 (1+2+3+4=10) Εἶναι ἀριθμὸς ποὺ ἀποτελοῦσε σημεῖο ἀναφορὰς στὴν πυθαγόρεια διδασκαλία. Τὸ ἀποτέλεσμα αὐτὸ ἦταν προαπαιτούμενο γιὰ τὴν ὀρθὴ ἀπόδοση τῆς Τετρακτύος καὶ ἐπιτεύχθηκε μὲ γεωμετρικὸ τρόπο μόνο ὅταν θεωρήσαμε πὼς τὸ σχῆμα της βασίζεται στὸ Χρυσὸ τρίγωνο. Τὰ μέχρις ἐδῶ στοιχεῖα θὰ μποροῦσαν νὰ εἶναι ἀρκετὰ γιὰ νὰ ἐπιβεβαιώσουν τὴν ἀρχικὴ μᾶς εἰκασία. Οἱ ἀποκαλύψεις ὅμως δὲν σταματοῦν.
