Τετρακτὺς καὶ Πυθαγόρεια Μουσική Κλίμακα
Τετρακτὺς καὶ ἡ ἐνδιάμεση τιμὴ δ
Ἀπό τὸ βιβλίο…

Για την σπουδαιότητα τοῦ ἀριθμοῦ δ ἔχει γίνει ἐκτενὴς ἀναφορά. Τὸ ὅτι ἡ τιμὴ του προκύπτει σὰν λόγος εὐθυγράμμων τμημάτων τοῦ χρυσοῦ τριγώνου, πιστοποιεῖ καὶ τὴν ἀποδοχὴ τῆς Τετρακτύος ὡς πρὸς τὴν ἀξία της, καθὼς τὸ χρυσὸ τρίγωνο ἐμπεριέχεται στὸ σχέδιο τῆς Τετρακτύος.
Ἐδῶ θὰ δοῦμε πὼς ὁ μοναδικὸς ἐλεγκτὴς συμπαντικῆς συμβατότητας θὰ μᾶς δώσει τὸν ἐνδιάμεσο ἀριθμὸ δ καὶ σὰν τιμή εὐθυγράμμου τμήματος .
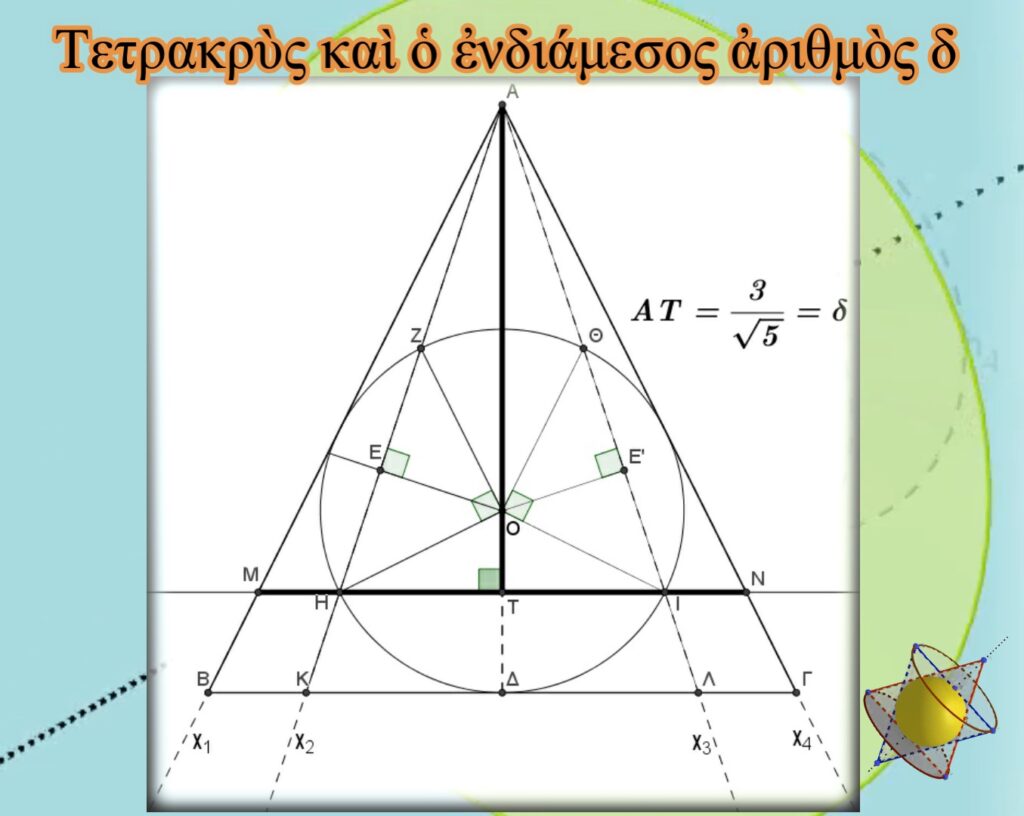
Τὰ σημεῖα Η καὶ Ι τῶν δύο κάτω ἀκτινῶν τῆς Τετρακτύος ὁρίζουν εὐθεία κάθετη στὸ ὕψος ΑΔ τοῦ Χρυσοῦ Τριγώνου, ἡ ὁποία τὸ τέμνει στὸ σημεῖο Τ.
Ἀποδεικνύεται (ἐδῶ) πὼς τὸ ΑΤ εὐθύγραμμο τμῆμα ἔχει τιμὴ ἴση μὲ τὸν ἐνδιάμεσο ἀριθμὸ δ.
Ἡ τιμὴ τοῦ ἐνδιάμεσου ἀριθμοῦ δ ποὺ βρέθηκε, μαζὶ μὲ τὴν ἀκολουθία Δν=δ·φν χρησιμοποιήθηκαν γιὰ νὰ προσεγγίσουμε τὴν τιμὴ τοῦ ἀριθμοῦ π (ἀπόκλιση τῆς τάξης τοῦ 10-11). Μάλιστα, γιὰ ν=12 εἴδαμε ὅτι Δ12=432,0041666… Μὴ ξεχνᾶμε ὅτι μὲ γνώμονα τὴν Τετρακτύν, ἐπίσης ἔχουμε: 33=27 καὶ 27·24=432.
Ἀπὸ τὴν ἐμφανὴ ὁμοιότητα τῶν τριγώνων ΑΒΓ καὶ ΑΜΝ καὶ ἐπειδὴ ΑΔ=ΒΓ ἀπὸ κατασκευῆς, εὔκολα προκύπτει πὼς ΑΤ=ΜΝ.
Εἶναι λοιπὸν πολὺ σημαντικὸ τὸ ὅτι γιὰ πρώτη φορὰ καὶ μὲ βάση τὴ σχέση ΑΤ=ΜΝ=δ, ποὺ ἀποδείξαμε, συνδέονται μεταξὺ τους τὸ Χρυσὸ Τρίγωνο καὶ ἡ ἐνδιάμεση τιμὴ δ, μὲ τὴν Τετρακτύν τοῦ Πυθαγόρα, μὲ τὴν μουσικὴ του κλίμακα, μὲ τὸν ἀριθμὸ 12 (ἀριθμὸς βημάτων ὁλοκλήρωσης τῆς μουσικῆς κλίμακας) καὶ μὲ τὴν τιμὴ 432, ποὺ ἀποτελοῦσε τιμὴ ἀναφορὰς γιὰ τὴν συχνότητα τῆς νότας Λά.

