Τετρακτὺς καὶ Πυθαγόρεια Μουσική Κλίμακα
Τετρακτὺς καὶ περιοδικότητα 12 βημάτων
Ἀπό τὸ βιβλίο…

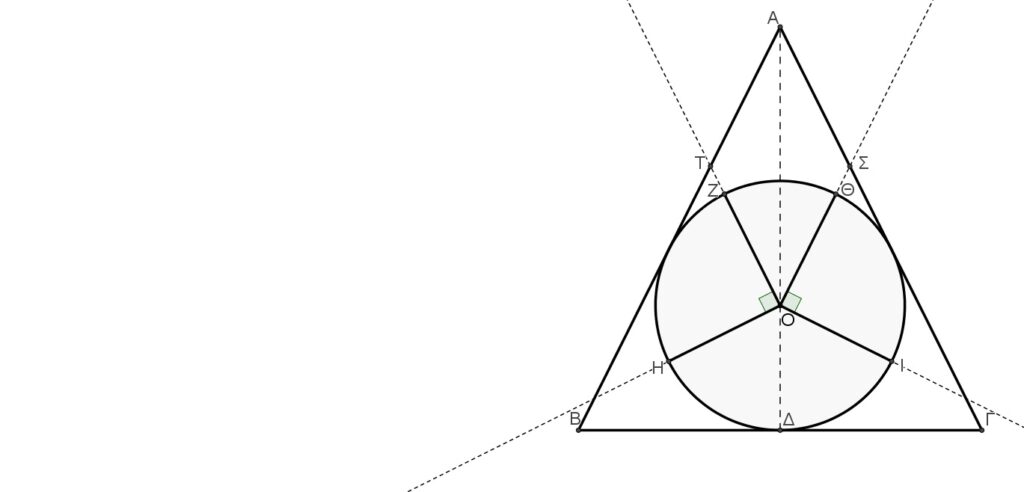
Θὰ συνεχίσουμε τὴν ὑπέρβαση προσθέτοντας μιὰ ἀκόμη διάσταση στὴν Τετρακτύν. Τὸ ἰσοσκελὲς τρίγωνο, μὲ τὸ ὁποῖο τὴν ἀποδώσαμε, ἔχει ἕναν ἄξονα συμμετρίας, τὸ ὕψος πρὸς τὴν βάση του, τὴν εὐθεία δηλαδὴ ποὺ περνάει ἀπὸ τὰ σημεῖα Α καὶ Δ. Ἐὰν περιστρέψουμε τὴν Τετρακτύν γύρω ἀπὸ αὐτὸν τὸν ἄξονα, τότε θὰ προκύψει ἕνας πολὺ συγκεκριμένος κῶνος. Αὐτὸς θὰ ἔχει ὕψος ΑΔ ἴσο μὲ τὸν ἀριθμὸ φ, κυκλικὴ βάση μὲ διάμετρο ΒΓ ἴση ἐπίσης μὲ τὸν ἀριθμὸ φ καὶ πλευρὰ λ ποὺ θὰ εἶναι ἴση μὲ λ=ΑΒ=(√5∙φ)/2 . Θὰ μπορούσαμε νὰ τοποθετήσουμε καὶ μία σφαίρα μὲ διάμετρο ἴση μὲ τὴ μονάδα ἐντὸς τοῦ κώνου (μοναδιαία σφαίρα). Τότε, ὅλες οἱ γενέτειρες τοῦ κώνου θὰ ἐφάπτονταν τῆς μοναδιαίας σφαίρας.
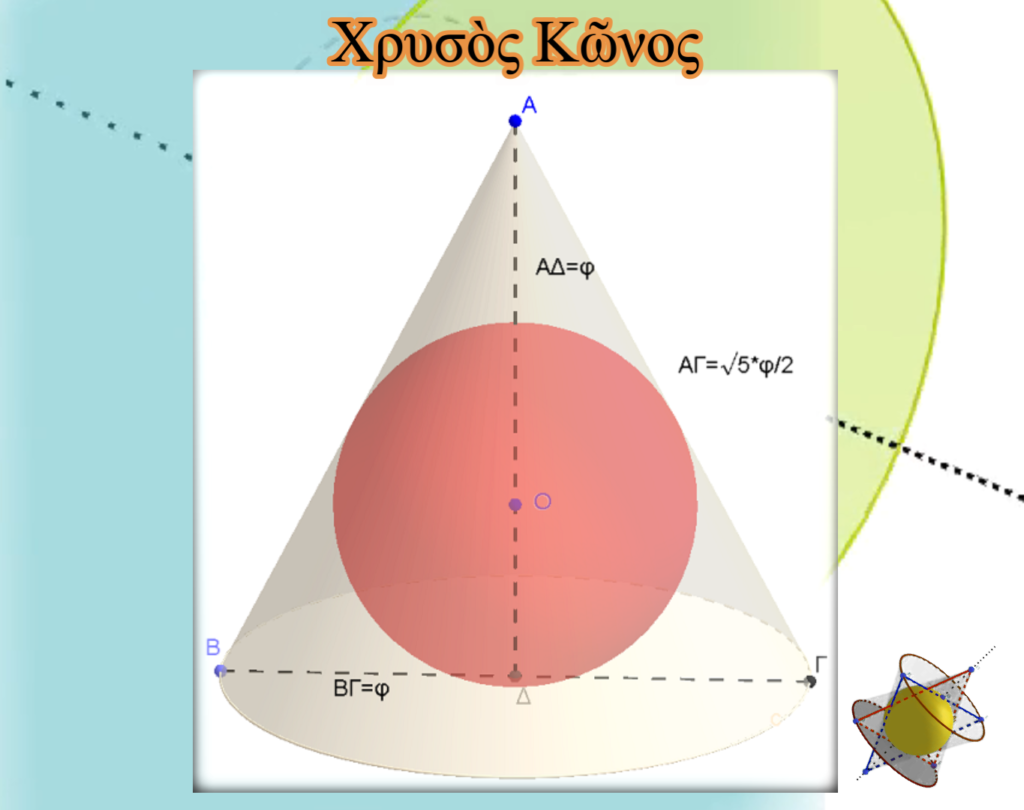
Τὸν κῶνο αὐτὸν θὰ τὸν ἀναπτύξουμε, σὰν νὰ θέλαμε νὰ τὸν κατασκευάσουμε ἀπὸ χαρτόνι, ὅπως στὸ ἑπόμενο σχῆμα.
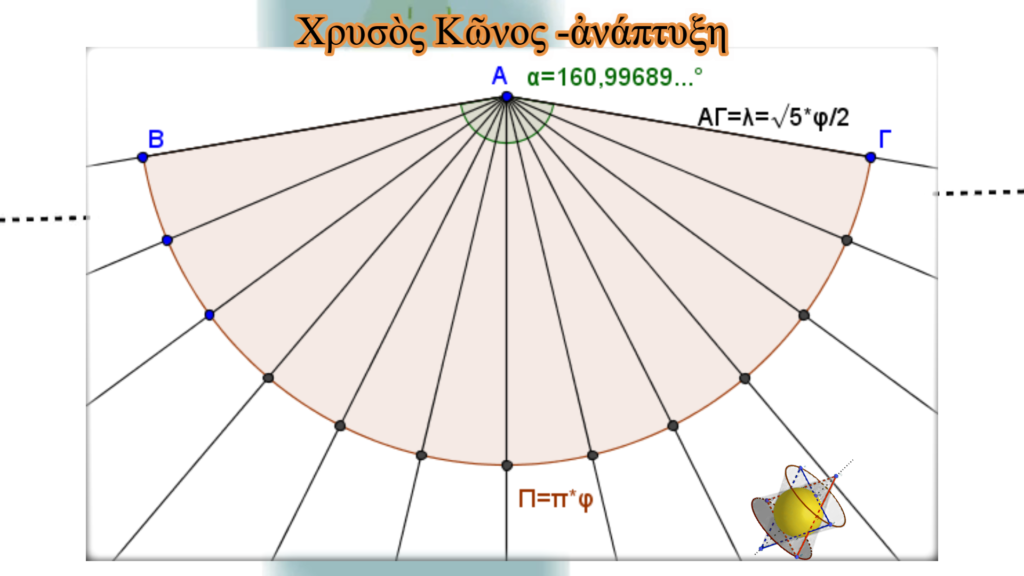
Τὸ σχῆμα εἶναι ἕνας κυκλικὸς τομέας μὲ ἀκτίνα ΑΓ ἴση μὲ τὴν πλευρὰ τοῦ κώνου λ= (√5∙φ)/2 καὶ κυκλικὸ τόξο ἴσο σὲ μῆκος μὲ τὴν περίμετρο τῆς κυκλικῆς βάσης τοῦ κώνου Π=π∙φ.
Θὰ ὑπολογίσουμε τὴν γωνία ΒΑ ̂Γ.
Ἡ περίμετρος ὁλόκληρου τοῦ κύκλου θὰ εἶναι ΠΚ=2πλ=2π (√5 φ)/2=√5·πφ καὶ ἀντιστοιχεῖ σὲ επίκεντρη γωνία τῶν 360°, ἐνῶ ἡ περίμετρος τοῦ τόξου, ὅπως εἴπαμε εἶναι ἴση μὲ π∙φ. Γιὰ τὴν ἀντίστοιχη γωνία θὰ ἔχουμε ΒΑ ̂Γ=(360°∙πφ)/(√5 πφ)=160,99689…° ἢ ὀρθότερα 160° 59′ 49”. Γιὰ τὶς ἀνάγκες τῆς παρουσίασης καὶ γιὰ νὰ μπορέσουμε νὰ κατανοήσουμε εὐκολώτερα τὰ σημαντικώτατα δεδομένα ποὺ θὰ ἀκολουθήσουν, ἔστω καὶ παράτυπα, καὶ παρόλο ποὺ ἡ γωνία δίνεται σὲ μοῖρες, θὰ τὴν ἀποδώσουμε σὲ δεκαδικὴ μορφή.
Ἐκτελοῦμε μιὰ ἁπλὴ διαίρεση τῆς τιμῆς τῆς γωνίας ποὺ βρήκαμε, μὲ τὴν τιμὴ τοῦ ἐνδιάμεσου ἀριθμοῦ δ καὶ βρίσκουμε…
(ΒΑ ̂Γ)/δ=(160,99689…)/(1,34164…)=120=12∙10
Ἐντυπωσιακό. Μιὰ γωνία μετρημένη σὲ μοῖρες (ἔστω καὶ σὲ δεκαδικὴ μορφή, γιὰ νὰ μπορεῖ νὰ ἐκτελεστεῖ ἡ διαίρεση), ἡ ὁποία προέκυψε ἀπὸ τὴν Τετρακτύν τοῦ Πυθαγόρα ὅταν αὐτὴ θεωρήθηκε Χρυσὸ Τρίγωνο, διαιρούμενη μὲ τὸν ἐνδιάμεσο ἀριθμὸ δ, μᾶς ἔδωσε αὐτούσιο τὸν ἀριθμὸ ἑκατὸν εἴκοσι. Μᾶς ἔδωσε δώδεκα φορὲς τὸν ἀριθμὸ δέκα, ποὺ ἀποτελεῖ θεμελιώδη ἀριθμὸ στὴν Πυθαγόρεια ἀριθμοσοφία καὶ σημεῖο ἀναφορὰς τῆς Τετρακτύος. Μᾶς ἔδωσε τὸν ἀριθμὸ τῶν βημάτων γιὰ τὴν ὁλοκλήρωση τῆς μουσικῆς κλίμακας.
Εἶναι ἀποτέλεσμα ποὺ προκύπτει καὶ ἀλγεβρικά. Ἐπειδὴ δ=3/√5 ἔχουμε:
(ΒΑ ̂Γ)/δ=(360°∙πφ√5)/(√5 πφ3)=(12∙3∙10)/3=12∙10
Ὅλα αὐτὰ ὅμως, ἔγιναν ἐντυπωσιακὰ γιατὶ ὁ κύκλος εἶναι χωρισμένος σὲ 360 μέρη καὶ ὄχι μὲ κάποιον ἄλλο τρόπο. Εἶναι αὐτὸ τυχαῖο; Μποροῦμε νὰ τὸ δεχθοῦμε σὰν σύμπτωση; Θὰ τὸ ἐρευνήσουμε.

Ἀποδεχόμενοι τὴν ἐγκυρότητα τῶν ἀναγραφόμενων τοῦ σύγχρονου φυσικοῦ καὶ ἀστρονόμου κύριου Διονύση Σιμόπουλου (πηγὴ: ἱστοσελίδα τῆς Wikipedia), θὰ πρέπει νὰ δεχθοῦμε ὅτι ὁ κύκλος γιὰ πρώτη φορὰ διαχωρίστηκε σὲ 360 μέρη ἀπὸ τὸν Ἵππαρχο τὸν Ρόδιο (πέρ. 190 π.Χ. -120 π.Χ.). Δὲν πρόκειται γιὰ ἕνα τυχαῖο ἱστορικὸ πρόσωπο. Γιὰ πολλοὺς πρόκειται γιὰ τὸν πατέρα τῆς Ἀστρολογίας. Μὲ γνώσεις ἀπὸ τοὺς ἀρχαίους Βαβυλώνιους, μὲ πρόσβαση στὴν Ἀλεξανδρινὴ βιβλιοθήκη ἀλλὰ καὶ μὲ πολλὲς δικὲς του μελέτες, μόνο τυχαία δὲν μπορεῖ νὰ θεωρηθεῖ ἡ ἐπιλογὴ αὐτή. Ἐκτὸς αὐτοῦ, ὁ κατοπινὸς διαχωρισμὸς τῆς κάθε μοίρας σὲ 60 πρῶτα καὶ κάθε ἑνὸς ἀπὸ αὐτὰ σὲ 60 δεύτερα, ἐνισχύει τὴν ἄποψη αὐτή. Ἡ κάθε μοίρα χωρίζεται συνολικὰ σὲ 60∙60=3.600 ΄΄, ὅπου καὶ πάλι ἔχουμε: 3.600=10∙360.
Τὸ μεγαλύτερο μέρος τοῦ ἔργου τοῦ κάηκε στὸν ἐμπρησμὸ τῆς Ἀλεξανδρινῆς Βιβλιοθήκης. Παρόλα αὐτὰ μπορεῖ νὰ θεωρηθεῖ πιθανὸν ὅτι ὁ Ίππαρχος ὁ Ρόδιος ἦταν γνώστης τῶν παραπάνω ἀναγραφόμενων καὶ αὐτὰ νὰ τὸν ὁδήγησαν στὴν ἀναγκαία ἐπιλογὴ – ἀποδοχὴ διαχωρισμοῦ τοῦ κύκλου σὲ 360°.
Τὰ παραπάνω ἀποδεδειγμένα στοιχεῖα εἶναι ἀρκετὰ γιὰ νὰ τεκμηριώσουν τὴν ἄποψη μου ὅτι τὸ σχῆμα τῆς πυθαγόρειας Τετρακτύος εἶναι αὐτὸ τοῦ χρυσοῦ τριγώνου. Δὲν εἶναι ὅμως τὰ μοναδικά.

