Τετρακτὺς καὶ Πυθαγόρεια Μουσική Κλίμακα
Εἰσαγωγή
Ἀπό τὸ βιβλίο…

Ὁ πρῶτος ποὺ ἀσχολήθηκε μὲ τὶς ἁρμονικὲς ταλαντώσεις καὶ τὴ μουσικὴ κλίμακα ἦταν ὁ Πυθαγόρας ὁ Σάμιος. Πρόκειται γιὰ μιὰ ἀπὸ τὶς κορυφαῖες, παγκόσμιες καὶ διαχρονικὲς προσωπικότητες. Στὴν ἱστορία ἔμεινε γνωστὸς κυρίως γιὰ τὸ γεωμετρικὸ θεώρημα ποὺ ἔχει τὸ ὄνομα του. Δὲν ἦταν ὅμως μόνο αὐτό. Ἱστορικὲς πηγὲς ἀναφέρουν ὅτι μαθήτευσε σὲ σχολὲς καὶ ἱερατεῖα, τόσο στὴν ἀρχαία Περσέπολη, ὅσο καὶ στὴν ἀρχαία Αἴγυπτο. Ἐκεῖ μυήθηκε στὴν ἐπιστήμη τῆς Γεωμετρίας, καθὼς καὶ στὴν μοναδικότητα τῆς ἀναλογίας τῆς χρυσῆς τομῆς καὶ τοῦ ἀριθμοῦ φ.
Ὁ Πυθαγόρας γνώριζε ὅτι τὸ μῆκος τῆς χορδῆς εἶναι ἀντιστρόφως ἀνάλογο μὲ τὴ συχνότητα τοῦ παραγόμενου ἤχου. Κατόπιν πειραμάτων καὶ μαθηματικῶν ὑπολογισμῶν, κατέληξε ὅτι γιὰ κάθε ἦχο ποὺ προκύπτει ἀπὸ συγκεκριμένου μήκους χορδή, ὁ πλέον συγγενικὸς ἦχος εἶναι αὐτὸς ὁ ὁποῖος προέρχεται ἀπὸ τὰ 2/3 αὐτῆς. Ἡ ἀντίστοιχη συχνότητα τοῦ ἤχου, ἑπομένως, θὰ εἶναι ἴση μὲ τὰ 3/2 τῆς ἀρχικῆς.

Δυστυχῶς, δὲν γνωρίζουμε μέχρι πιὸ σημεῖο ἔρευνας ἔφτασε ὁ Πυθαγόρας, καθὼς ὅπως λέγεται, δὲν ἄφησε γραπτὲς μαρτυρίες. Πάντως εἶναι παράδοξο ποὺ ὁ Ραφαήλ στὸ ἔργο του, « Ἡ Σχολὴ τῶν Ἀθηνῶν» στὸ Βατικανό, τὸν παριστάνει περιτριγυρισμένο ἀπὸ μαθητές του , κατὰ τὴν συγγραφὴ βιβλίου του. Εἶναι παράδοξο καὶ εἰρωνικό, ποὺ τὸ ἔργο αὐτὸ βρίσκεται στὸν ἴδιο κτιριακὸ συγκρότημα μὲ τὴν βιβλιοθήκη τοῦ Βατικανοῦ, στὴν ὁποία, παρόλο ποὺ εἴμαστε πολίτες τοῦ δυτικοῦ κόσμου καὶ πολιτισμοῦ, ποὺ πυλῶνες τους εἶναι ἡ δημοκρατία καὶ ἡ ἐλευθερία, μᾶς ἀπαγορεύεται ἡ πρόσβαση.
Ἔτσι, στηριζόμενοι μόνο σὲ ὅσα μποροῦμε νὰ γνωρίζουμε, θὰ ξεκινήσουμε ἀπὸ μία ἀρχικὴ νότα. Ἡ ἑπόμενη θὰ ἔχει συχνότητα κατὰ 3/2 φορὲς μεγαλύτερη τῆς ἀρχικῆς.
Συνεχίζοντας μὲ τὸν ἴδιο ἁπλὸ τρόπο, κατόπιν 12 ἐπαναλήψεων καὶ ἀφοῦ πρῶτα περάσουμε ἀπὸ ὅλες τὶς ἐνδιάμεσες νότες, θὰ φτάσουμε στὴν ἀντίστοιχη μὲ τὴν ἀρχικὴ νότα, ἀλλὰ κατὰ ἑπτὰ (7) ὀκτάβες ὑψηλότερης συχνότητας.
Γιὰ νὰ μποροῦμε νὰ ἔχουμε τὶς ἐμφανιζόμενες νότες ἐντὸς ὁρίων κλίμακας, διαιροῦμε ὅποτε χρειάζεται τὴν προκύπτουσα συχνότητα ἐπιπλέων μὲ τὸν ἀριθμὸ 2.
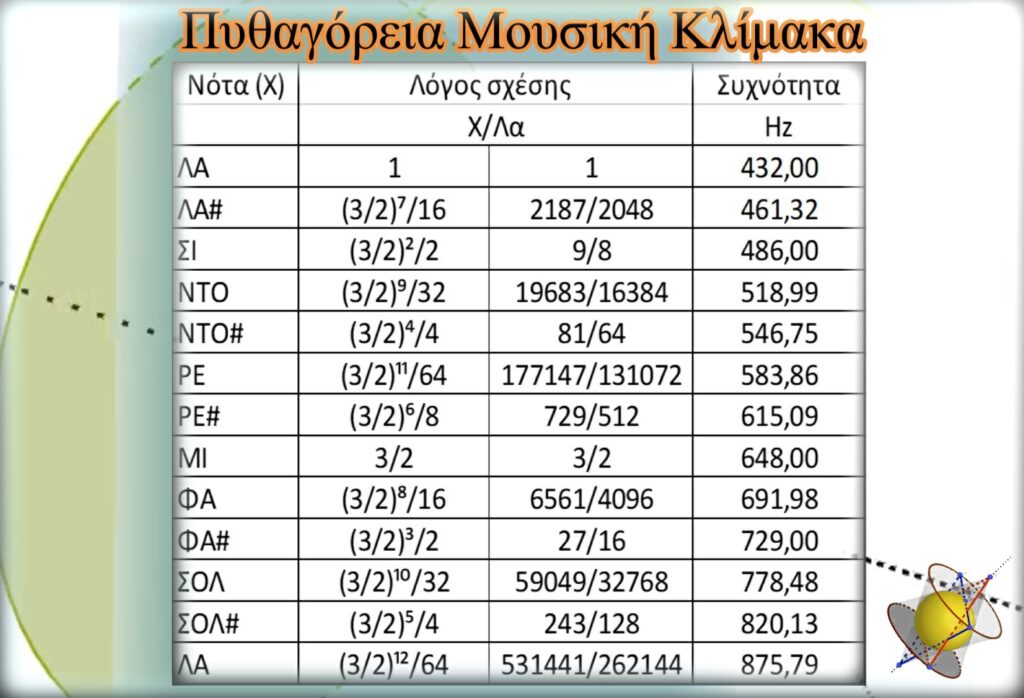
Τὰ πρῶτα σημαντικὰ συμπεράσματα, ποὺ προκύπτουν ἀπὸ τὴν Πυθαγόρεια Μουσικὴ Κλίμακα, εἶναι τὰ ἀκόλουθα.
– Εἶναι φανερὸ ὅτι ἡ μουσικὴ κλίμακα ἀντιμετωπίζεται πρώτη φορὰ σὰν ἕνα φυσικὸ ἐξελικτικὸ φαινόμενο. Εἶναι πρώτη φορὰ ἐκ τῶν πραγμάτων, ὅπου ἀποδεικνύεται ὅτι τὸ φαινόμενο αὐτὸ ἐκτελεῖ ἕναν πλήρη ἐξελικτικὸ κύκλο σὲ δώδεκα βήματα. Εἶναι κάτι ποὺ ἀποδείχτηκε καὶ ἐπισημάνθηκε ἐμφατικὰ στὴν ἔρευνα γιὰ τὸν τετραγωνισμὸ τοῦ κύκλου, μὲ τὴ χρήση τοῦ ἀριθμοῦ φ καὶ τῆς ἀκολουθίας του.
– Εἶναι φανερὸ ὅτι ἡ ἐξέλιξη τῆς μουσικῆς κλίμακας στηρίζεται σὲ γεωμετρικὴ πρόοδο, στὴ συγκεκριμένη περίπτωση μὲ λόγο τὸν ἀριθμὸ 3/2.
– Μετὰ ἀπὸ δώδεκα ἐξελικτικὰ βήματα παρατηροῦμε ὅτι τὸ πηλίκο τῶν συχνοτήτων τελικής-αρχικής νότας δὲν εἶναι ἀκριβῶς ἴσο μὲ τὸν ἀκέραιο ἀριθμὸ 2. Εἶναι ἴσο μὲ 531441/262144=2,0272865… Θὰ λέγαμε ὅτι «φλερτάρει» μὲ τὴν ἀκεραιότητα, χωρὶς νὰ τὸ ἐπιτυγχάνει, ὅπως ἀκριβῶς τὸ εἴδαμε καὶ στὴν μελέτη τῆς γεωμετρικῆς προόδου τοῦ ἀριθμοῦ φ.
Γιατὶ ὅμως αὐτὸ συμβαίνει;
Ἡ ἀπάντηση βρίσκεται στὸ ὅτι ἀντιμετωπίσαμε τὴν μεταβολὴ τῆς συχνότητας τῶν ἤχων σὰν φυσικὸ ἐξελικτικὸ φαινόμενο. Ὅπως σὲ ὅλα τὰ φυσικὰ ἐξελικτικὰ φαινόμενα, ἔτσι καὶ ἐδῶ ὑπεισέρχεται ἡ ἐπίδραση τοῦ χρόνου. Αὐτό, θὰ τὸ δοῦμε νὰ ἐπαναλαμβάνεται στὸ μουσικὸ συμπαντικὸ μοντέλο ποὺ θὰ μᾶς ὑποδείξει ἡ Τετρακτύς.
Γιὰ τὴ συνέχεια θὰ δοῦμε πὼς ἡ Τετρακτύς μᾶς δίνει τὰ διαπιστευτήρια τῆς γιὰ τὴν τιμὴ 3/2 σὰν λόγο, ἀλλὰ καὶ σὰν ἀριθμό.

